[Final Project] Inferring Space from Sensorimotor Dependencies

Documentation	Slides	iPython notebook

Approach

We consider an organism equipped with sensors, and try to infer the notion of “physical space” from its sensorimotor dependencies while assuming no prior knowledge of the organism about the fact there exists any such thing as a surrounding physical space.

Basically, the approach is the following one: we put ourselves in the organism brain’s shoes, all we can do is:

• issue motor commands (ex: brain tells the arm to move/tells the eyes to close themselves, etc…)
• observe environmental changes resulting from particular motor commands

and then we collect sensory inputs, which are twofold:

1. proprioceptive inputs:

   which are the sensory input of the organism that don’t change when the environment does (i.e. they don’t depend on the environment): this property is called proprioception.

   Examples:

   • the feeling of your limbs’ location in space, which enables you to know where they are without relying on environmental (e.g. visual) inputs.
   • in the following simulation: it will be the feeling of the location of the organism’s arm joints (ex: the position/configuration of its arm joints)

2. exteroceptive inputs:

   on the other hand, exteroceptive inputs are sensory inputs that may be modified by the environment: such a property is referred to as exteroception.

   Example:

   • visual inputs: when the luminance and aspect of the surrounding environment change, your sensory input related to vision changes as well, as you see different things (same situation in the subsequent simulation)

NB: through misuse of language, we will call proprioceptive (resp. exteroceptive) body all the body parts dedicated to proprioception (resp. exteroception).

---

Example: let’s consider the pokémon Haunter for example:

Here, proprioception encompasses locating his hands and body in space, and exteroception consists in visual inputs from its eyes and gustatory perception in his mouth. So the proprioceptive body in this case would be the information about the body the brain gets from proprioception only, i.e.: only its limbs location in space (not the visual/gustatory cues its gets from the environment via its eyes and mouth).

---

Then, to learn more about the physical space in which the organism is embedded, we focus on the exteroceptive sensors, since they are the ones that react the environmental changes. In particular, we pay close attention to compensable movements, that appear in situations like these:

• Step 0: a fixed exteroceptive sensor has a value (x) (ex: looking at an object in front of oneself, the sensors being the cone cells in the retina for instance)
• Step 1: an environmental change (dE) modifies this value (which can indeed be modified by environmental changes as the sensor is exteroceptive) and sets it to (y) (ex: the object moves (1) meter forward: it looks smaller, as it is farther)

• Step 2: one notices that there exists a certain motor command (dM) that can bring this exteroceptive value back to (x) (ex: the brain orders the legs to walk one meter forward, and then one sees the object looks exactly as big as before).

  So $dM$ compensates $dE$: in the $Motor × Environment$ manifold, adding $dE$ and then $dM$ to a given starting point $(M_0, E_0)$ (thus getting $(M_0+dM, E_0+dE)$) brings one back to the same sensory input! In other words: \(φ((M_0, E_0)) = φ((M_0+dM, E_0+dE))\)

These special compensable movements are exactly what stems from the notion of the physical space in the sensory inputs: in the previous example, it’s the notion of relative distance between the organism and the object in the surrounding world (hence a spatial property) that is the same in step 1 and step 2, and that causes the sensory input to be same.

So what we are actually interested in is computing the dimension of the rigid group of compensated movements (it should be the dimension of the Lie group of orthogonal transformations (3 translation and 3 rotations), i.e. 6 if the organism is embedded in a 3D-space).

To do so, we aim to compute the minimal number of parameters needed to describe the the variations in the exteroceptive inputs (and hence exteroceptive body, i.e. the states of the exteroceptive sensors (when the sensors are in different states, they won’t have the same value for the same environment (ex: an eye in two different positions won’t see the same thing when the environment doesn’t change, so the position of the eyes is part of their state)):

• when only the body moves

  • by “the body moves”, we mean that the exteroceptive body changes, as we will ignore proprioception right away from the start, since it doesn’t give us any information on the environment (and recall that what we are interested in are the compensable movements, i.e. changes of the exteroceptive body (resulting from motor commands) that can compensate changes of the environment. For example, if the environment is an object moving 1 meter forward, the organism’s body moving forward will compensate its visual input of the object. Similarly: if a light the organism is looking at becomes twice as bright, half-closing its eyes (with a diaphragm) will compensate its visual input too (since the doubled luminance will be halved).
• when only the environment changes
• when both the body and the environment change

with resort to dimension reduction methods. Indeed, it can be shown that:

\[d = p+e−b\]

where

• $d$ is the dimension of the space of compensated movements
• $p$ is the dimension of the space of sensory inputs obtained through variations of the motor commands only
• $e$ is the dimension of the space of sensory inputs obtained through variations of the environment only
• $e$ is the dimension of the space of sensory inputs obtained through variations of the motor commands and the environment alike.

How is the simulation of organism 1 conducted?

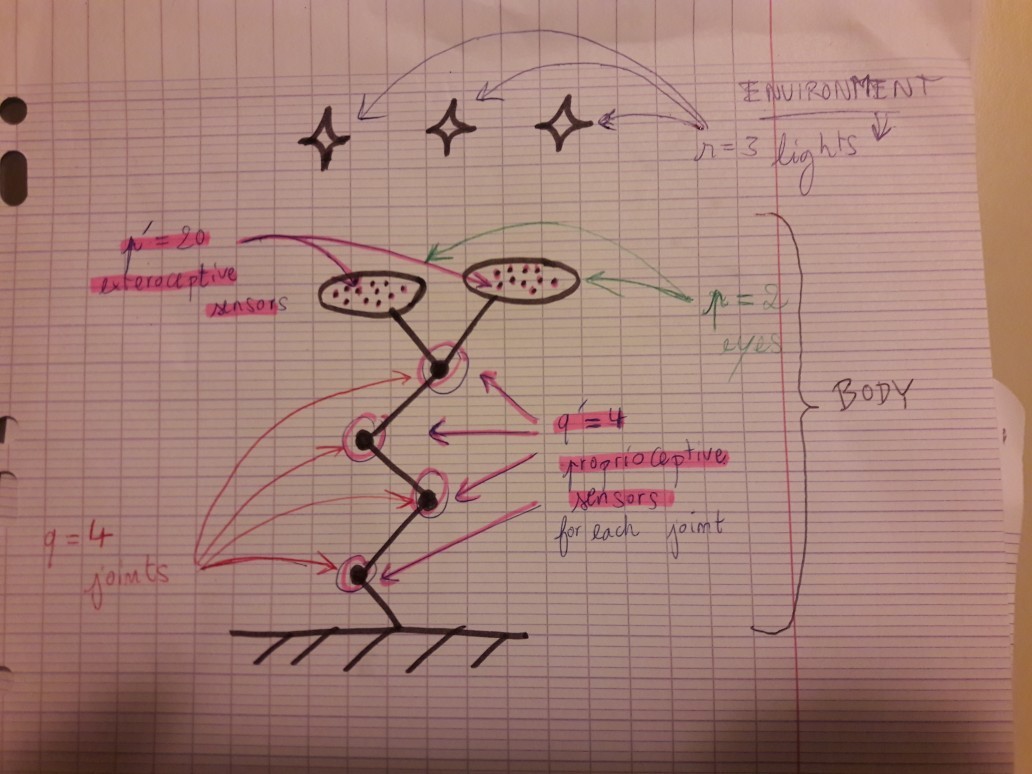
The situation is the following: organism 1 is an “arm with two eyes” comprised of:

• 4 joints (black dots in the drawing), each one equipped with 4 proprioceptive sensors
• 2 eyes, each one equipped, each one equipped with 20 exteroceptive (“retina-like”) sensors

and an environment constituted of 3 lights.

Recall that proprioceptive sensors are sensors that are NOT sensitive to changes of the environment, they only depend on the body (here: on the position of the joints), whereas exteroceptive may depend on the environment (here: the eyes’ sensors are sensitive to the luminance and position of the environmental lights).

Now, the motor commands are the commands the “brain” of the organism sends to its body (e.g.: «Move the second joint a little bit!»).