Is there something out there?
Inferring Space from Sensorimotor Dependencies
Kexin Ren & Younesse Kaddar
Based on D. Philipona, J. O’Regan, and J. Nadal’s 2003 article
Introduction: you said “space”?
I. Exteroception & Compensation
II. Mathematical formulation
III. Algorithm
V. Simulations and Beyond
Introduction: you said “space”?
high-dimensional sensory input vector$\qquad \overset{\text{Brain}}{\rightsquigarrow} \qquad \underbrace{\textit{space, attributes, ...}}_{\text{easier to visualize}}$
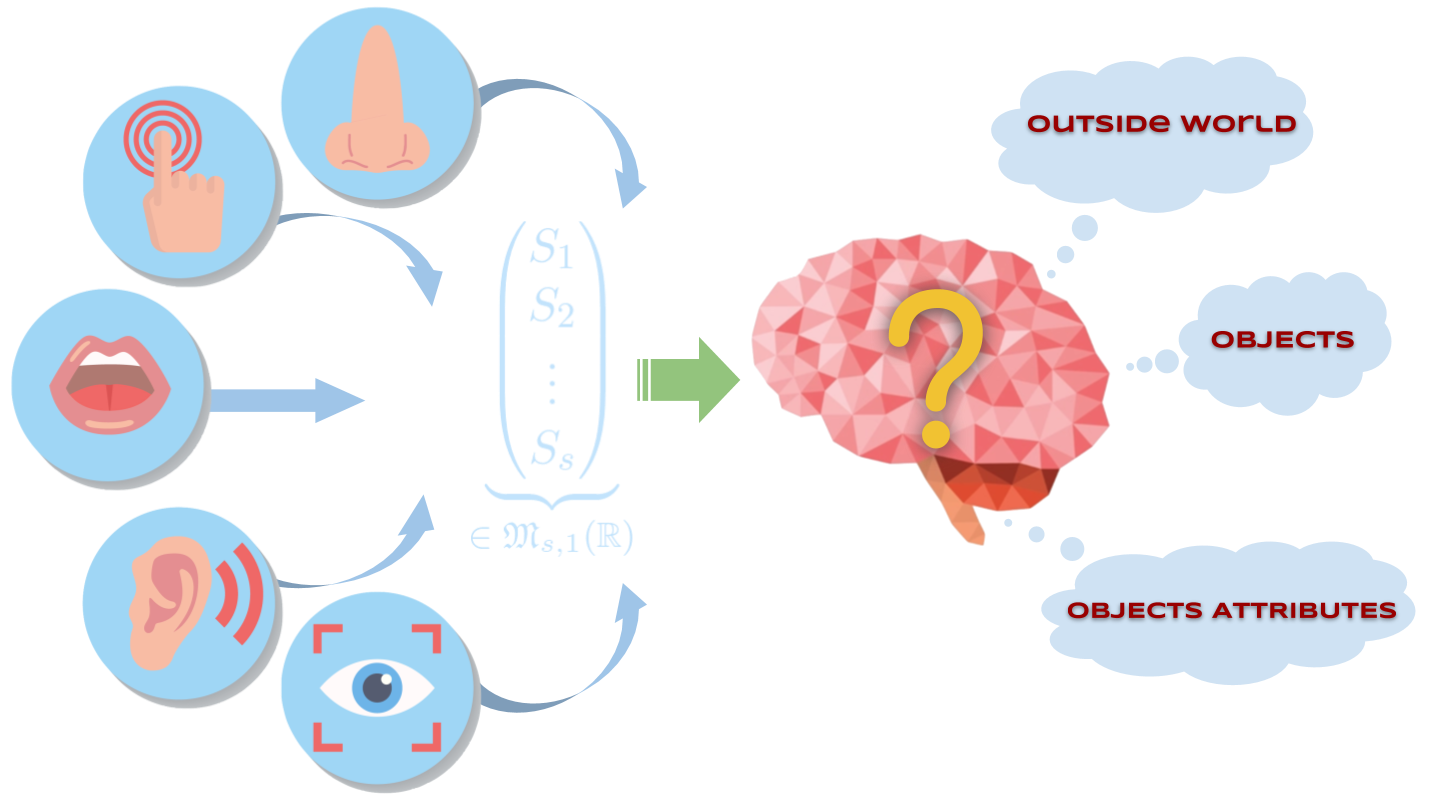
- All the brain can do:
-
-
issue motor commands
-
observe the resulting environmental changes
⟹ then collect sensory inputs
-
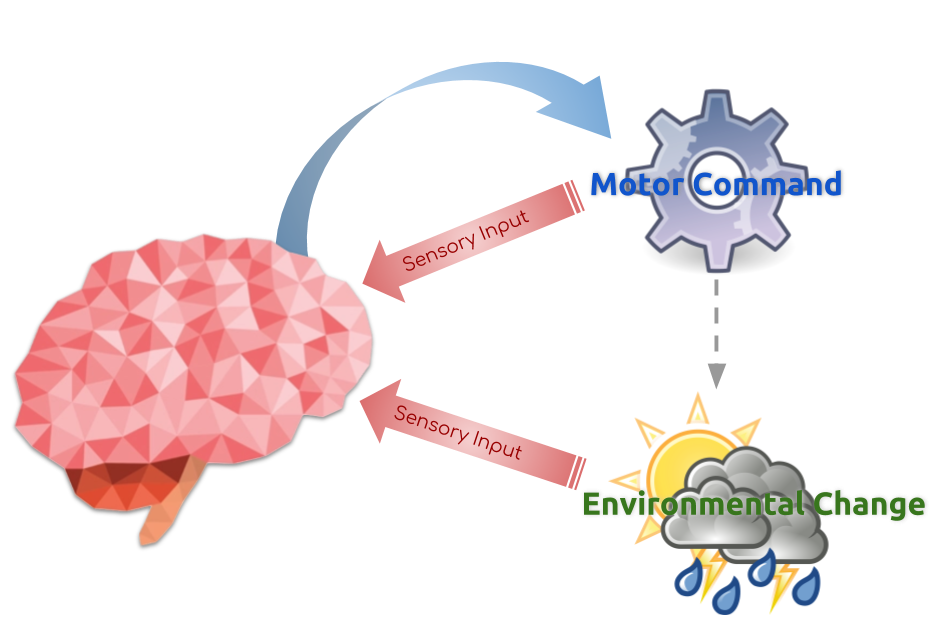
I. - Exteroception & Compensation
I.A Exteroception vs. Proprioception
| Sensory input | Definition |
|---|---|
| Proprioceptive | independent of the environment |
| Exteroceptive | dependent of the environment |
Example
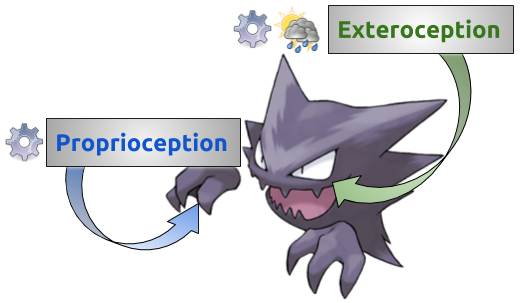
I.B - Compensated movements
- Compensated movements:
- Variations of the motor command and the environment that compensate one another.
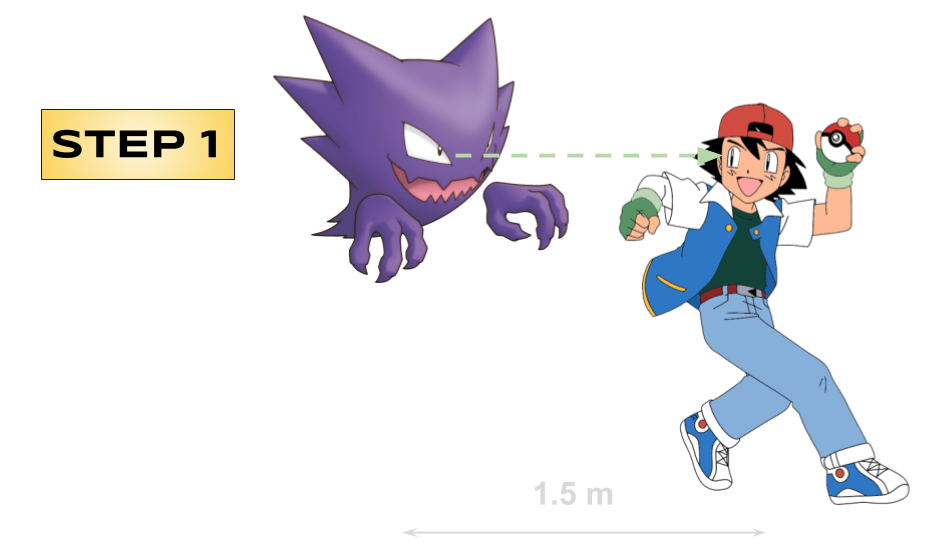

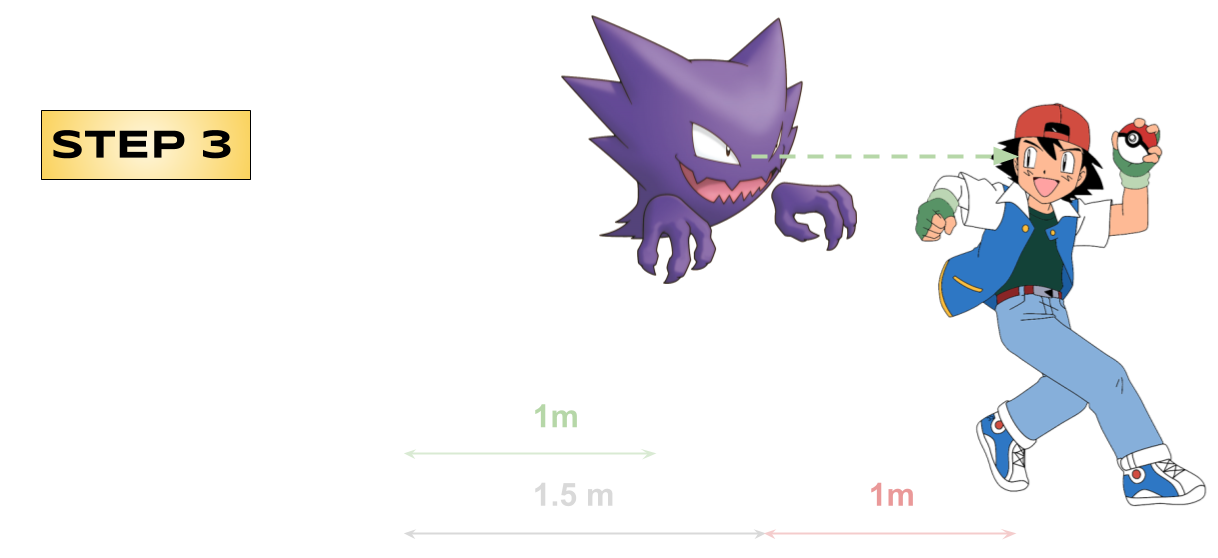
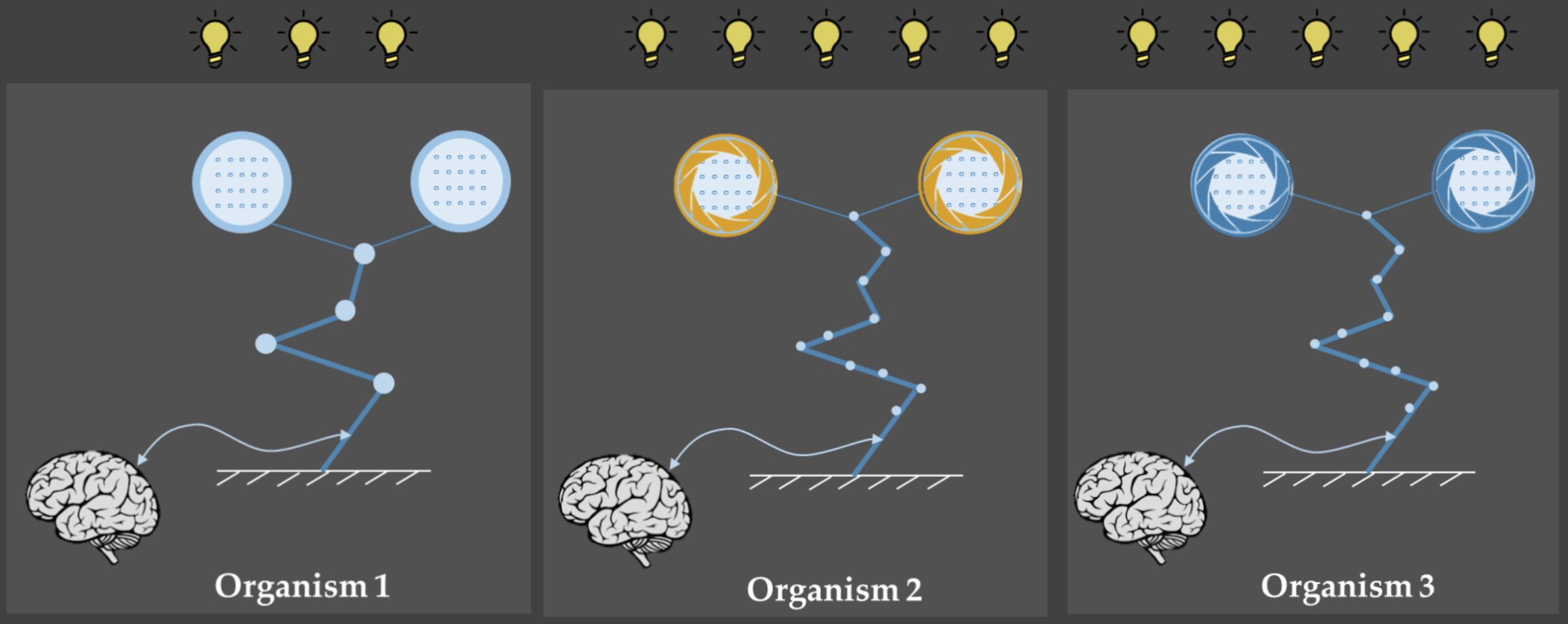
Organism 1
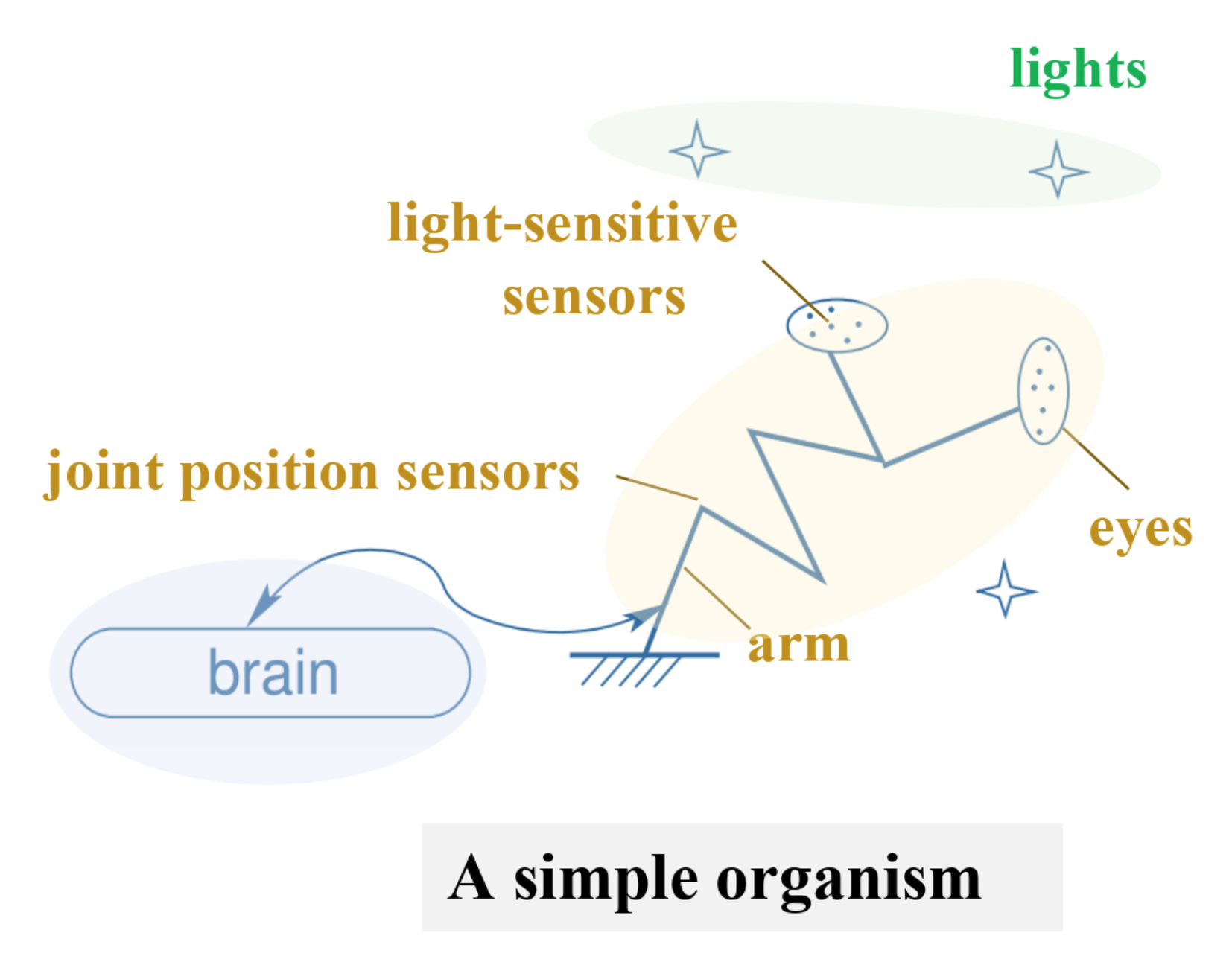
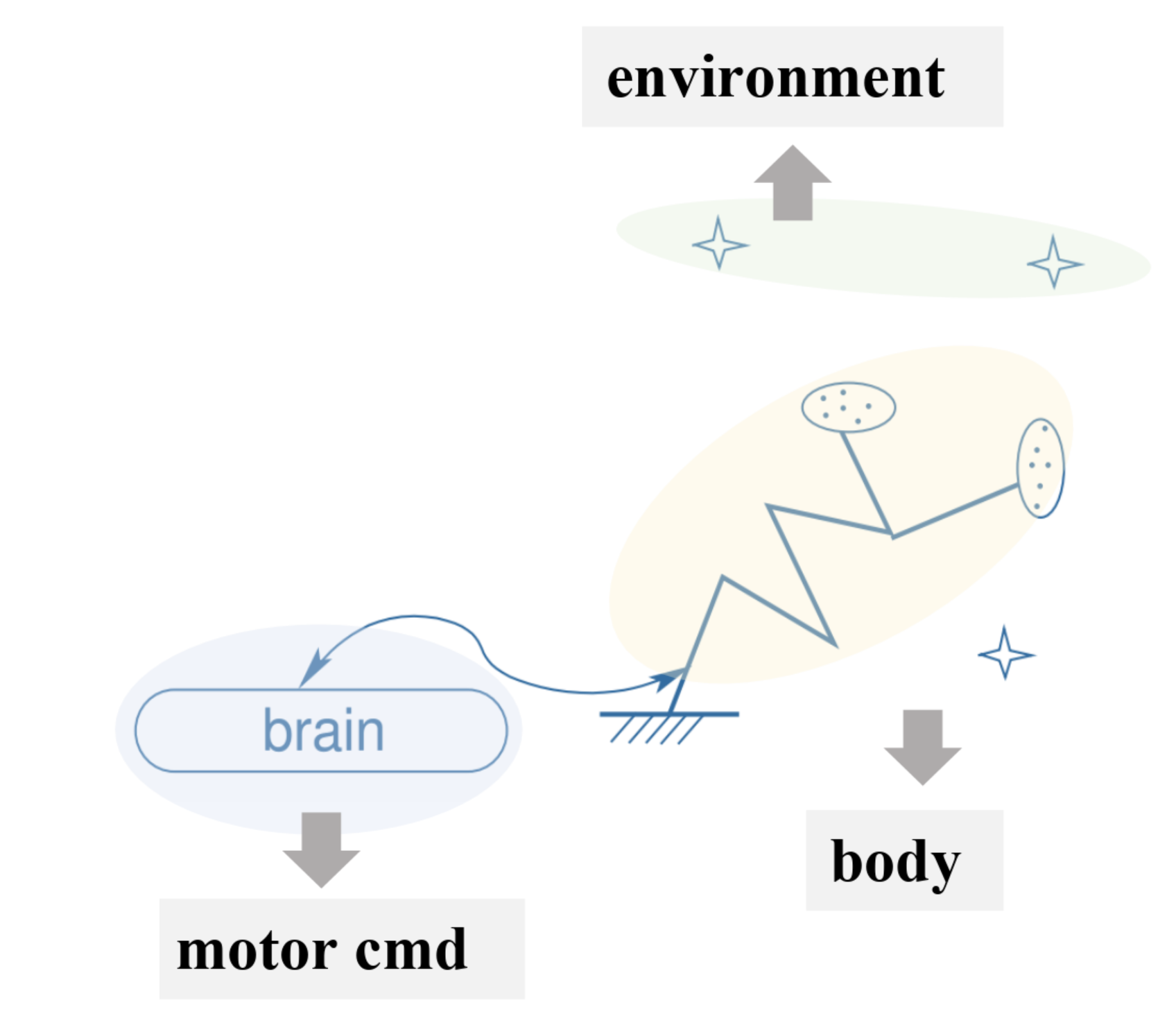
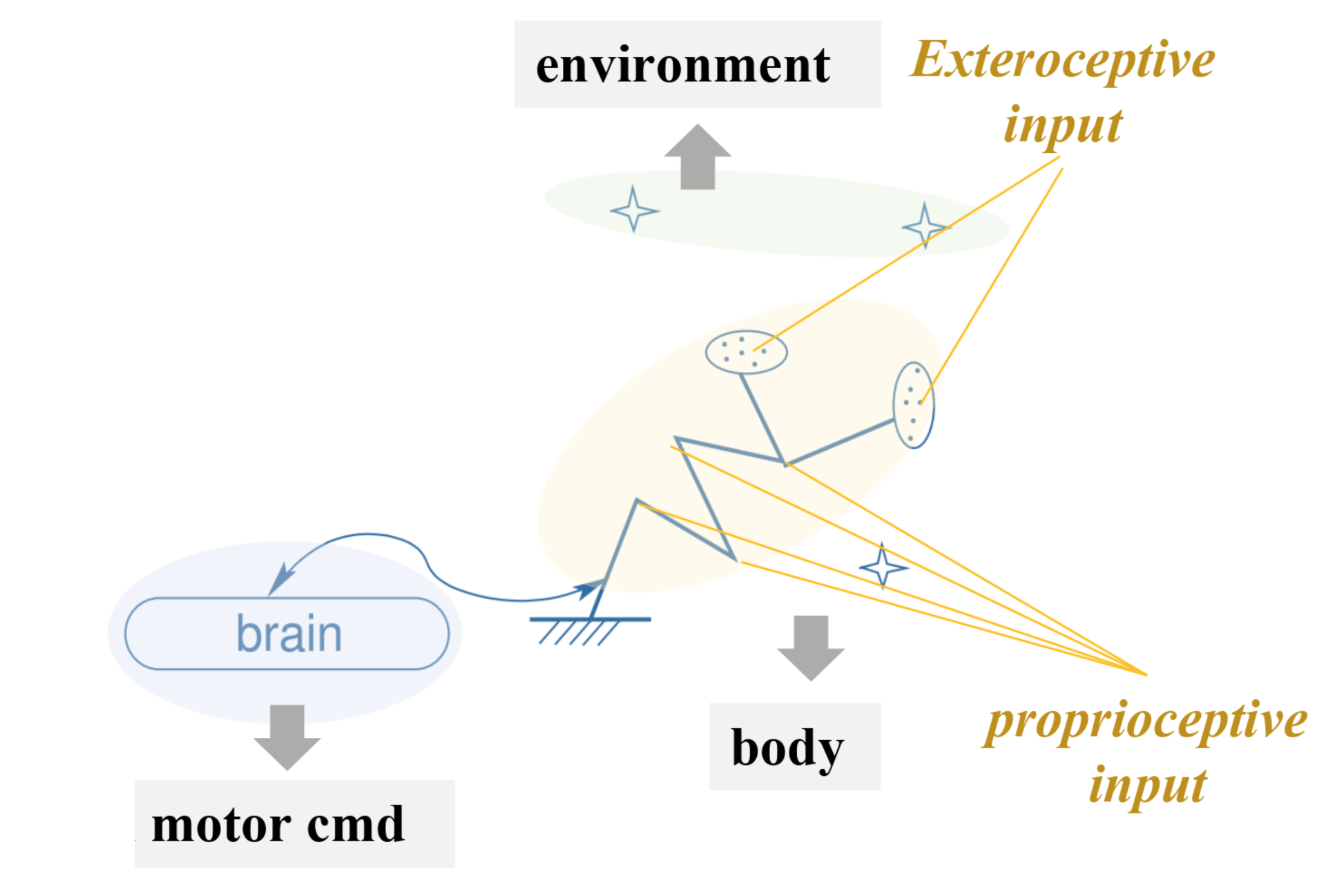
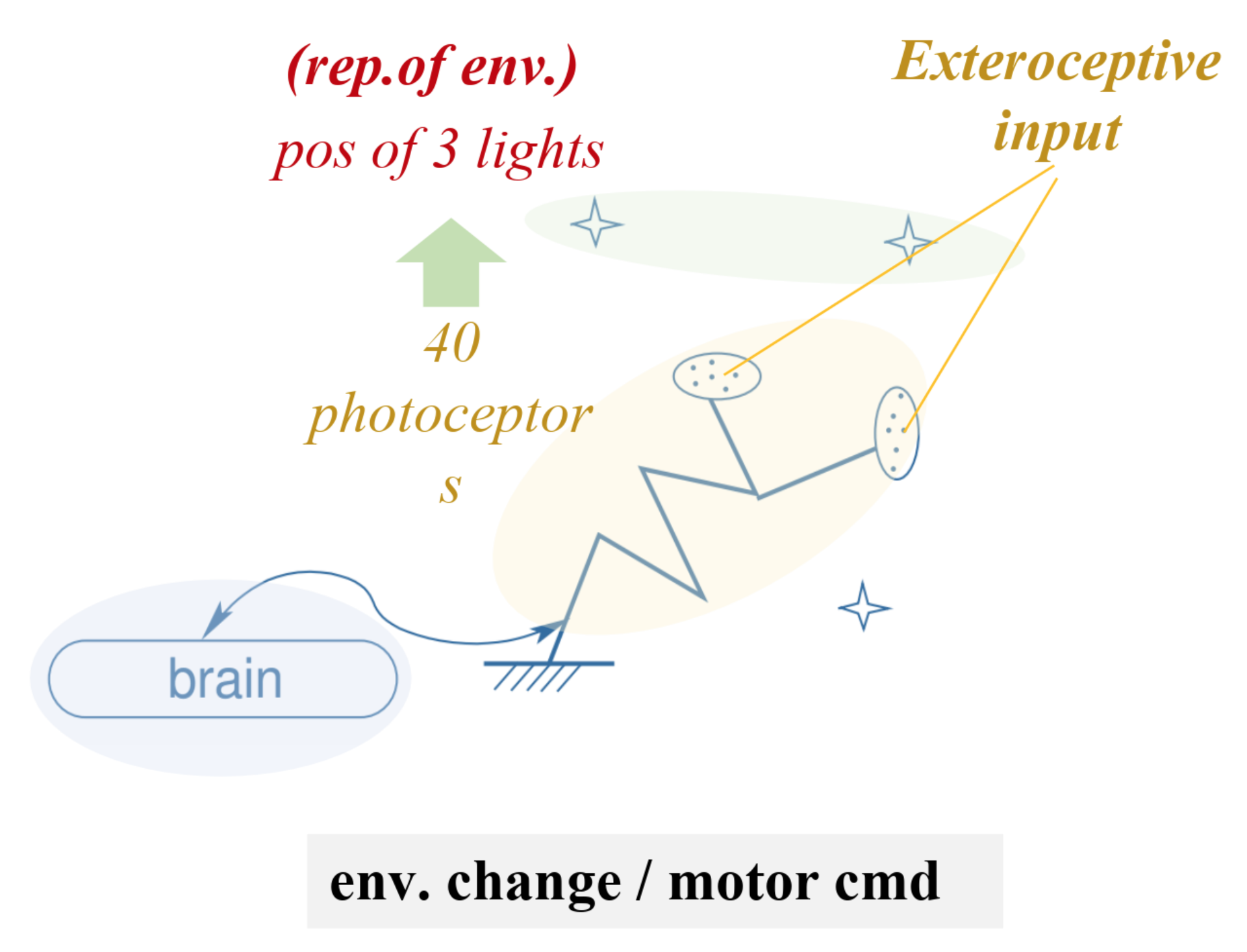

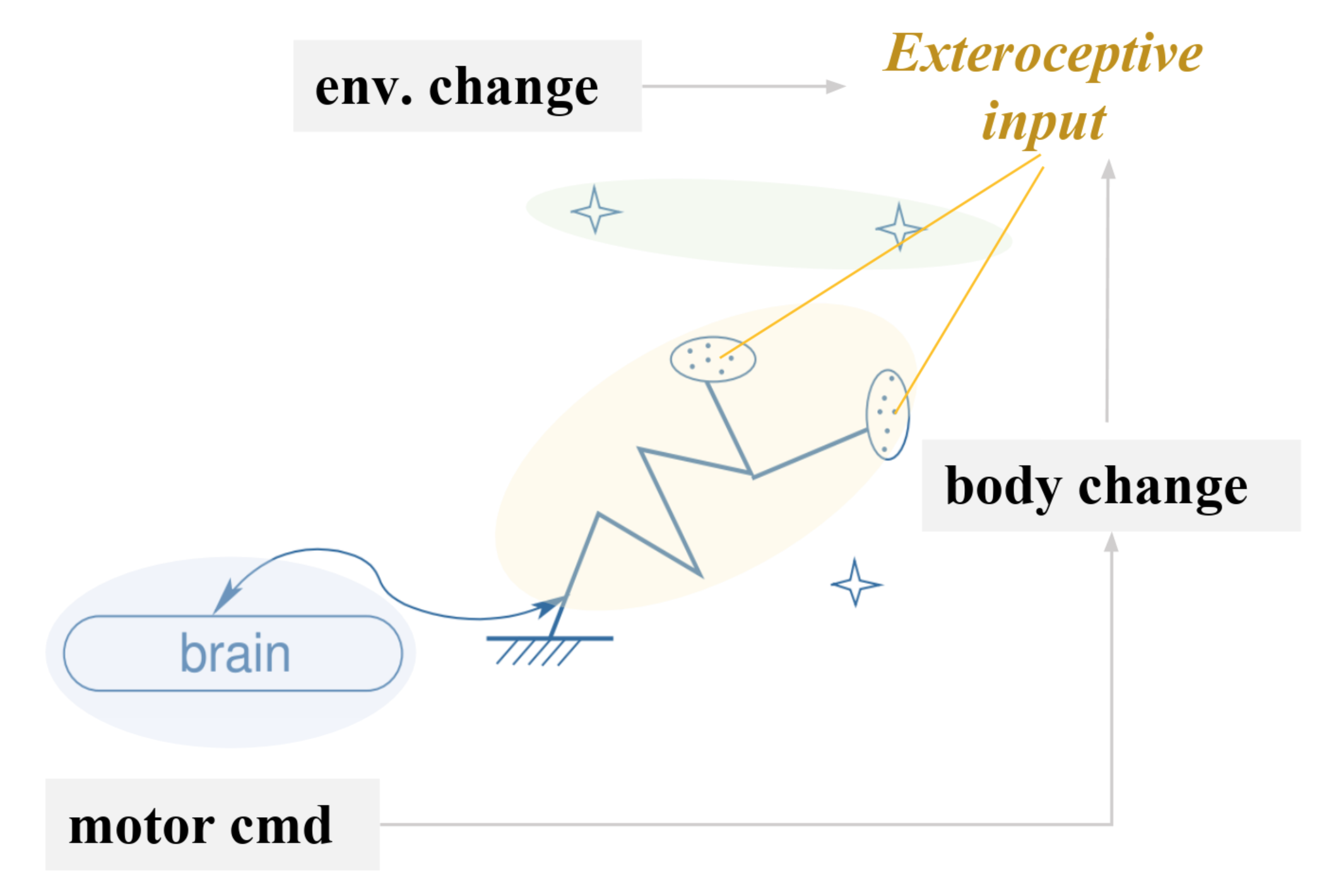
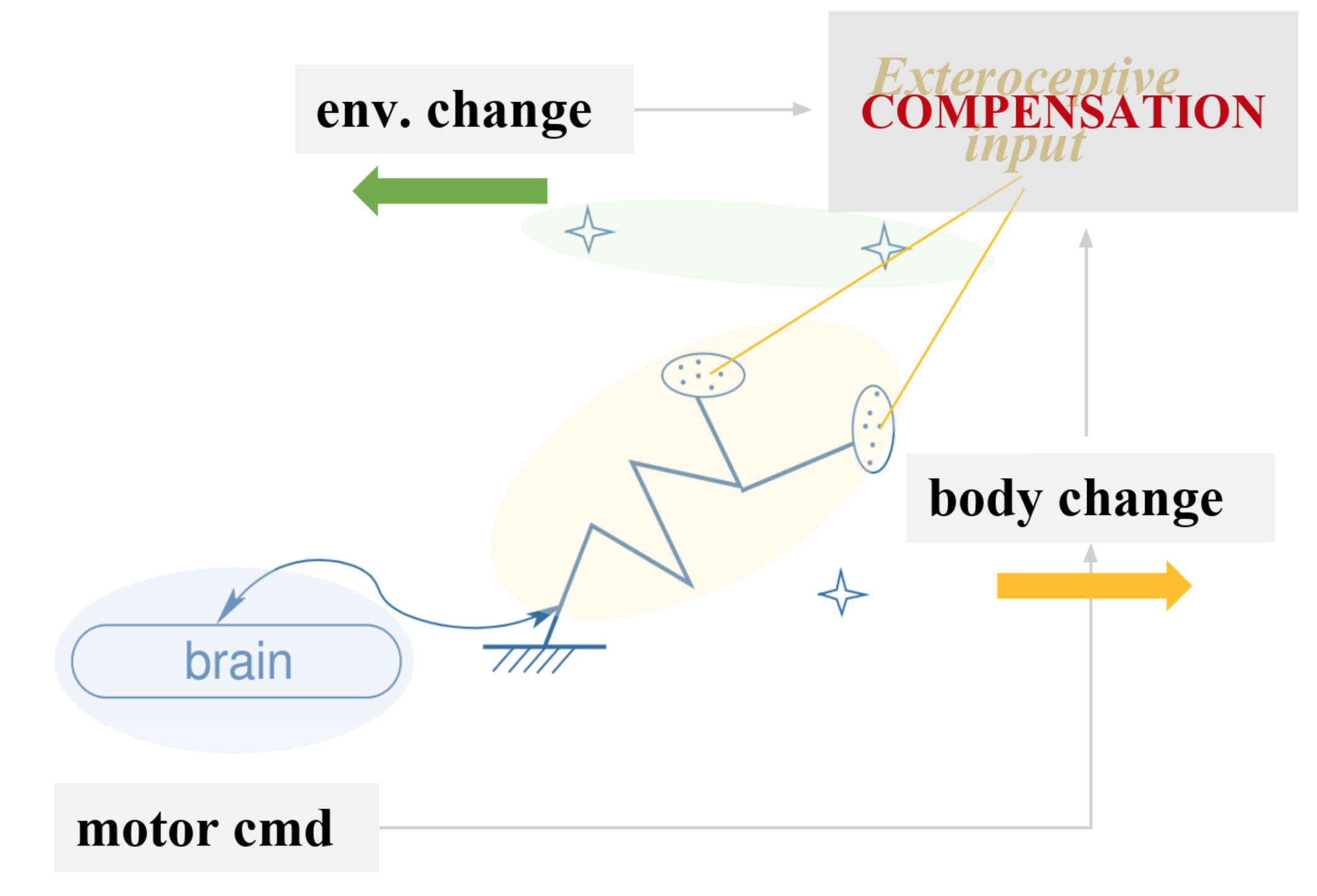
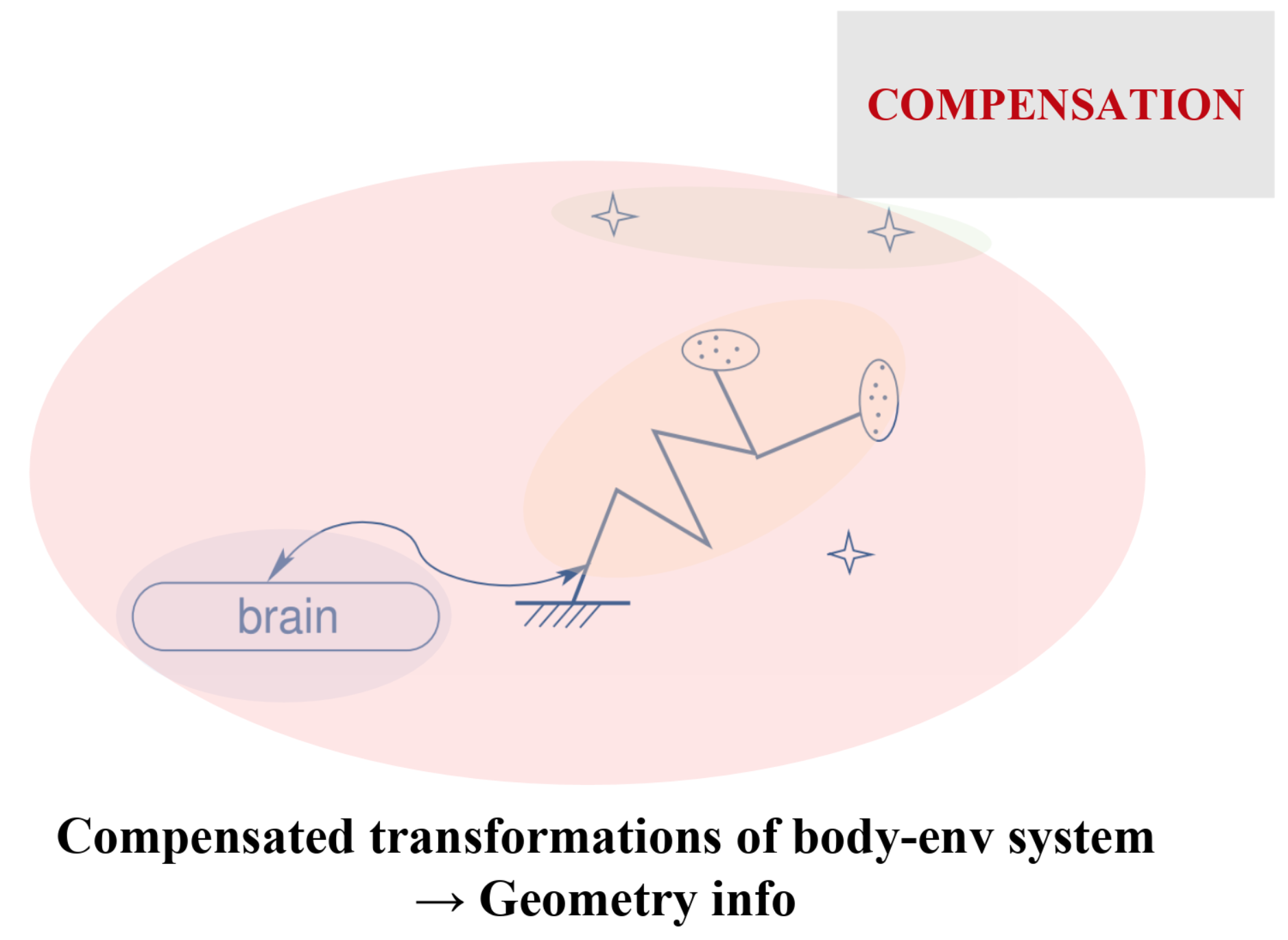
Compensable movements: exactly what stems from the notion of the physical space in the sensory inputs
So the true goal: computing the dimension of the rigid group of compensated movements.
II. Mathematical formulation
are manifolds of dimension $e, m$ and $s$ respectively such that:
$$\mathcal{S} = ψ(\mathcal{M} × \mathcal{E})$$
NB: We are only considering exteroceptive inputs, i.e. points $S^e ∈ \mathcal{S}$ s.t.:
Pushforward of $(M_0, E_0)$ by $ψ$
⟹ Tangent space at $S_0 ≝ ψ(M_0, E_0)$:
$$\lbrace dS \rbrace = \lbrace dS \rbrace_{dE=0} + \lbrace dS \rbrace_{dM=0}$$
Moreover:
- $\lbrace dS \rbrace_{dE=0}$ is the tangent space of $ψ(E_0, \mathcal{M})$ at $S_0$
- $\lbrace dS \rbrace_{dM=0}$ is the tangent space of $ψ(\mathcal{E}, M_0)$ at $S_0$
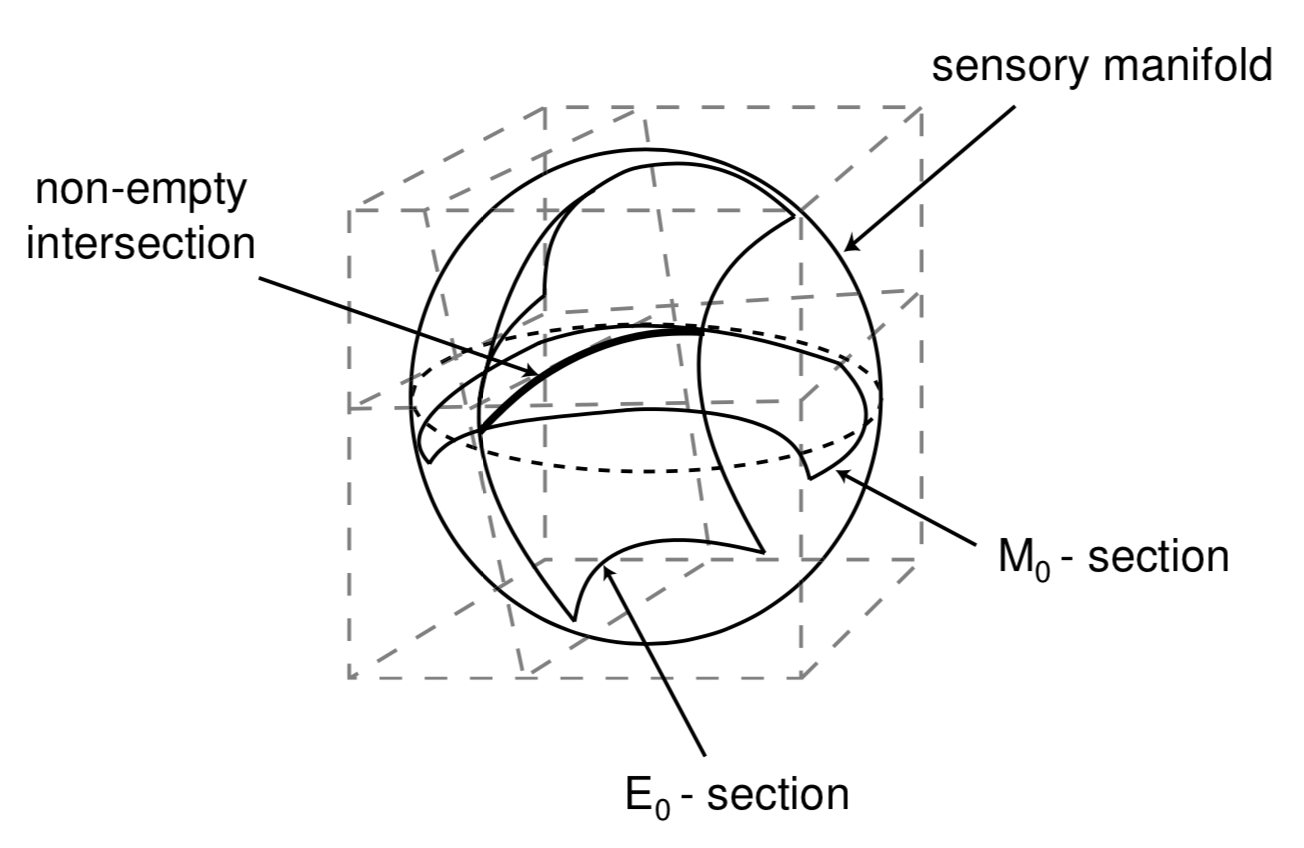
Along $\mathcal{C}(M_0, E_0)$: exteroceptive changes obtained by adding
- either $dE$
- or $dM$.
- Compensated (infinitesimal) movements:
- when infinitesimal changes along $\lbrace dS \rbrace_{dE=0}$ and $\lbrace dS \rbrace_{dM=0}$ compensate one another
- Dimension of the space of compensated movements:
- $$d ≝ \dim \underbrace{\lbrace dS_{dM=0} \mid ∃ dS_{dE=0}; dS_{dM=0} + dS_{dE=0} = 0 \rbrace}_{= \; \lbrace dS \rbrace_{dE=0} ∩ \lbrace dS \rbrace_{dM=0}} = \dim \mathcal{C}(M_0, E_0)$$
So by Grassmann formula:
$$\begin{align*} d \quad &≝ \quad \dim \lbrace dS \rbrace_{dE=0} ∩ \lbrace dS \rbrace_{dM=0}\\ \quad &= \quad \dim \lbrace dS \rbrace_{dE=0} + \dim \lbrace dS \rbrace_{dM=0} \\ \quad & \qquad - \dim \Big( \underbrace{\lbrace dS \rbrace_{dE=0} +\lbrace dS \rbrace_{dM=0}}_{= \lbrace dS \rbrace} \Big)\\ \\ \quad &= \quad \dim \lbrace dS \rbrace_{dE=0} + \dim \lbrace dS \rbrace_{dM=0} - \dim (\lbrace dS \rbrace) \end{align*}$$
Algorithm
Get rid of proprioceptive inputs # (these don't change when no motor command is issued and the environment changes) for "source" in [motor commands, environment, both]: Estimate dim(space of sensory inputs resulting from "source" variations) dim(compensated movements) = dim(inputs resulting from motor commands variations) + dim(inputs resulting from environment variations) - dim(inputs resulting from both variations)
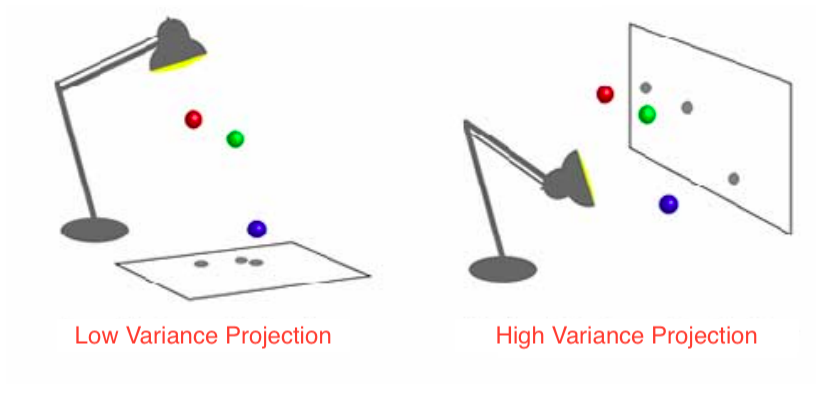
Principal Component Analysis
Goal: Find orthogonal axes onto which the variance of the data points under projection is maximal, i.e. find the best possible “angles” from which the data points are the most spread out.
Implementation
Neurorobotics_Project
│ index.md
│
└───sensorimotor_dependencies
│ │ __init__.py
│ │ utils.py
│ │ organisms.py
│
└───docs
│ ...
where
- utils.py ⟹ utility functions, among which dimension reduction algorithms
- organisms.py ⟹ Organism1(), Organism2(), Organism3()
Object-Oriented Programming
class Organism1: def __init__(self, seed=1, retina_size=1., M_size=M_size, E_size=E_size, nb_joints=nb_joints, nb_eyes=nb_eyes, nb_lights=nb_lights, extero=extero, proprio=proprio, nb_generating_motor_commands=nb_generating_motor_commands, nb_generating_env_positions=nb_generating_env_positions, neighborhood_size=neighborhood_size, sigma=σ): self.random = np.random.RandomState(seed) # [...] self.random_state = self.random.get_state() def get_sensory_inputs(self, M, E, QPaL=None): # [...] def get_proprioception(self): # [...] def get_variations(self): self.env_variations = ... self.mot_variations = ... self.env_mot_variations = ... def get_dimensions(self, dim_red='PCA'): self.get_proprioception() self.get_variations() # Now the number of degrees of freedom! self.dim_env = dim_reduction_dict[dim_red](self.env_variations) self.dim_extero = ... self.dim_env_extero = ... self.dim_rigid_group = ... return self.dim_rigid_group, self.dim_extero, self.dim_env, self.dim_env_extero
Other organisms
>>> O = organisms.Organism1(); O.get_dimensions() (4, 10, 5, 11) >>> print(str(O))
| Characteristics | Value |
|---|---|
| Dimension of motor commands | 40 |
| Dimension of environmental control vector | 40 |
| Dimension of proprioceptive inputs | 16 |
| Dimension of exteroceptive inputs | 40 |
| Number of eyes | 2 |
| Number of joints | 4 |
| Diaphragms | None |
| Number of lights | 3 |
| Light luminance | Fixed |
| Dimension for body § | 10 |
| Dimension for environment (e) | 5 |
| Dimension for both (b) | 11 |
| Dimension of group of compensated movements | 4 |
Some results
Varying retina_size (called var) values for different random seeds.