Final Report: Motion of Objects in Contact (Hopcroft & Wilfong)
Rapport: Mouvement d’Objets en Contact
Younesse Kaddar
Article étudié: Motion of Objects in Contact (J. Hopcroft & G. Wilfong, 1986)
Version PDF|Slides|Rapport en ligne
- |-|-
Introduction
Cet article fondateur fait un premier pas pour poser les bases d’une théorie des transformations d’objets, en démontrant le théorème suivant d’existence de mouvement en contact:
Théorème principal (Hopcroft & Wilfong):
S’il existe un mouvement de rotations et de translations entre deux configurations dans lesquelles un ensemble d’objets forment une composante connexe, alors il existe un mouvement entre ces deux configurations tel qu’à tout instant, les objets forment une composante connexe.
Ce que nous avons vu en cours sous la forme: “Dès qu’il y a un chemin dans l’espace libre, il y a un chemin au contact”.
De l’importance de la contractilité
Notons que si l’espace des configurations n’est pas contractile, le théorème ne s’applique pas (d’où le fait que nous autorisions des mouvements par translations), comme illustré par l’exemple suivant à un degré de liberté (l’espace des configurations est un cercle, en identifiant l’angle $2π-2θ$ et $2θ$):
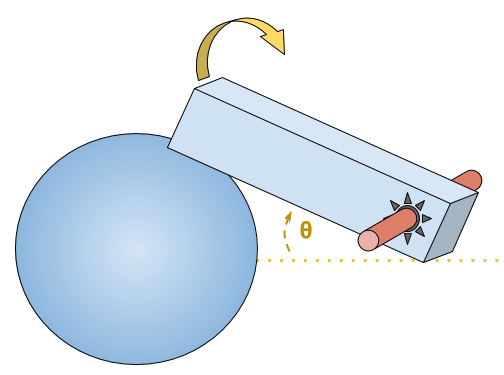
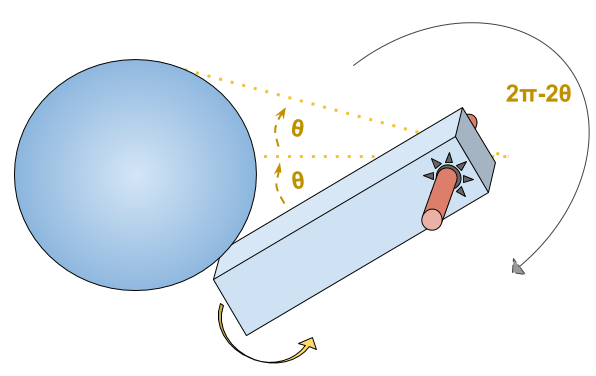
Le seul mouvement de l’angle $θ$ à l’angle $-θ$ ne garde pas la boule et la barre en contact.
Espace des configurations
Un objet est défini comme une partie convexe compacte de $ℝ^n$, égale à l’adhérence de son intérieur et bornée par un nombre fini de surfaces algébriques. La position et l’orientation de chaque objet est déterminée par une origine et un repère qui leur sont associés. Un objet composé est un objet constituté de plusieurs sous-objets, auquel on associe un graphe dont les sommets sont les objets et les arêtes lient deux sous-objets qui s’intersectent. Un des sous-objets est appelé la base: son origine est celle de l’objet composé. Tout objet peut être vu comme un objet composé à un seul sous-objet (sa base).
Une configuration est un vecteur de position et d’orientation des objets : ces vecteurs forment un espace de configuration. $B(x)$ (resp. $b(x)$) désignera la partie (resp. le point) de $ℝ^n$ occupé(e) par l’objet $B$ (resp. le point $b$) dans la configuration $x$.
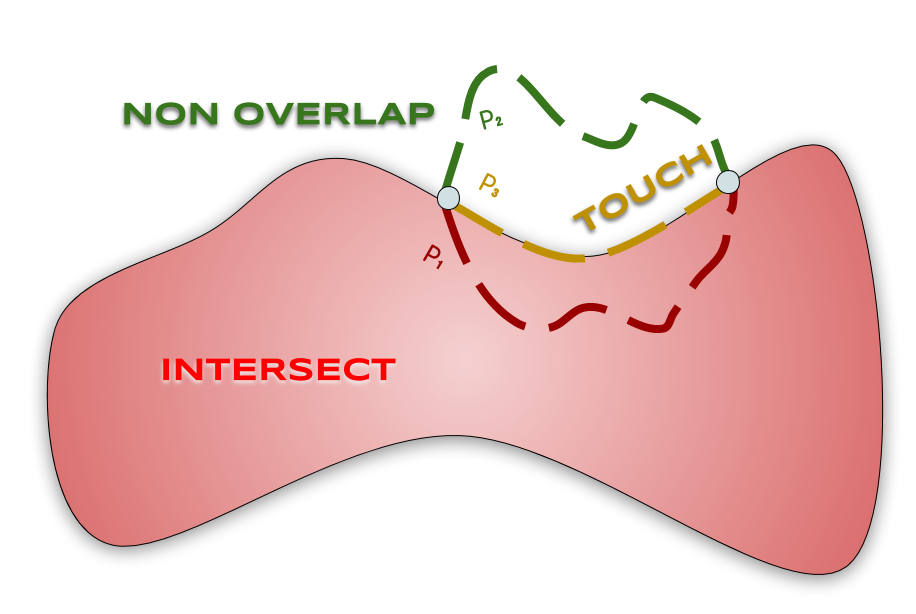
Si $x$ est une configuration, on dit que deux objets $B_i, B_j$:
| s’intersectent en $x$ | si $B_i(x) ∩ B_j(x) ≠ ∅$ |
| se chevauchent en $x$ | si $\int(B_i(x)) ∩ \int(B_j(x)) ≠ ∅$ |
| se touchent en $x$ | si $B_i(x) ∩ B_j(x) ≠ ∅ ∧ \int(B_i(x)) ∩ \int(B_j(x)) = ∅$ |
On définit les ensembles de configurations suivants:
| Ensemble | Configurations $x$ en lesquelles |
|---|---|
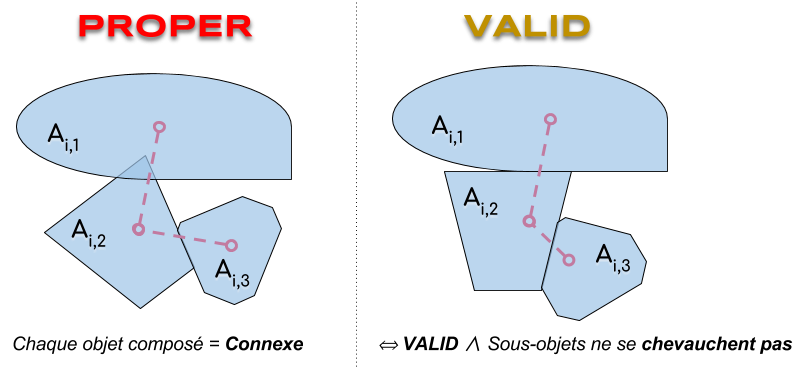
| PROPER | chaque objet composé a un graphe associé connexe (objets composés connexes et configurations propres) |
| VALID | chaque objet composé est connexe et est tel que tous les sous-objets qui s’intersectent se touchent (configurations valides) |
| Ensemble | Configurations $x$ valides telles qu’il existe (au moins) deux objets |
|---|---|
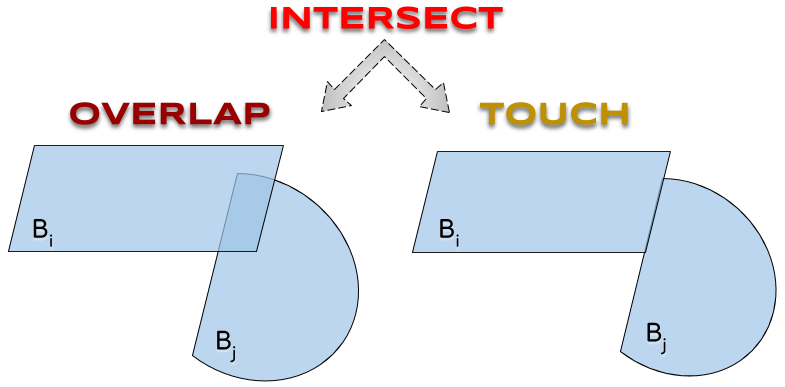
| INTERSECT | qui s’intersectent en $x$ |
| OVERLAP | qui se chevauchent en $x$ |
| TOUCH | qui se touchent en $x$ |
| Ensemble | Configurations $x$ propres telles que |
|---|---|
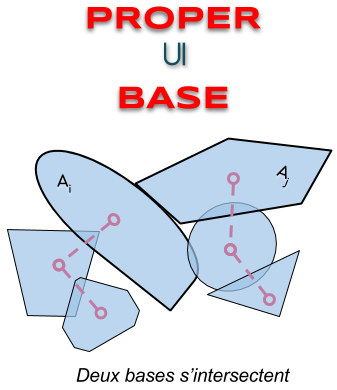
| BASE | la base d’un objet composé intersecte la base d’un autre (les bases sont indiquées en gras dans les schémas) |
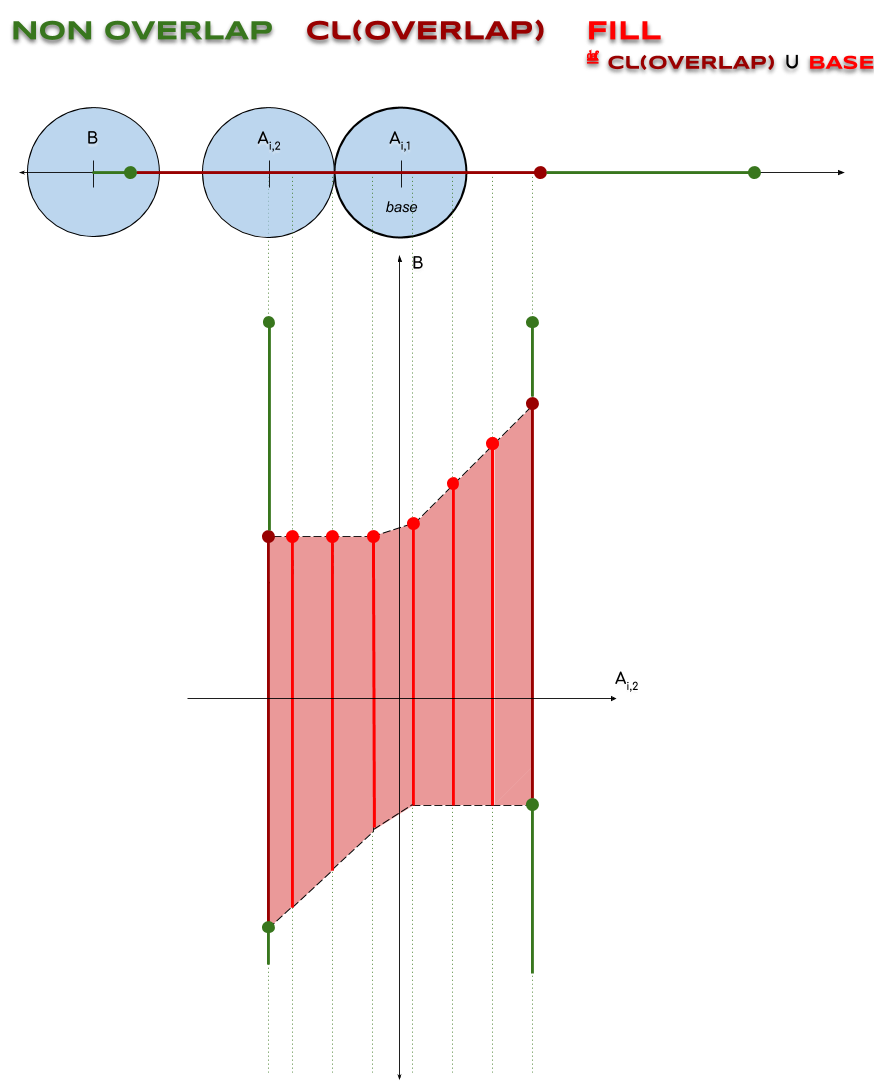
Enfin, on pose \(\NON ≝ \VALID\backslash\OVER \\ \FILL ≝ \cl(\OVER) ∪ \BASE\)
Pourquoi avoir recours à $\FILL$?
Comme le montre l’exemple suivant, où $A_i$ est un objet composé de base $A_{i, 1}$ fixe et $B$ un objet (mobile), $\NON ∪ \cl(\OVER)$ n’est pas contractile en général (ce qui est un point clé de la preuve): en ajoutant $\BASE$ (qui n’est pas inclus dans $\VALID$) à $\cl(\OVER)$, on rend $\FILL ≝ \cl(\OVER) ∪ \BASE$ contractile (voir le gif animé ici).
Détermination de TOUCH
Attention avec TOUCH
On pourrait penser que TOUCH est la frontière de INTERSECT, mais ce n’est pas le cas ! Considérer l’exemple suivant, avec deux objets $B_1$ et $B_2$ (voir le gif animé ici):
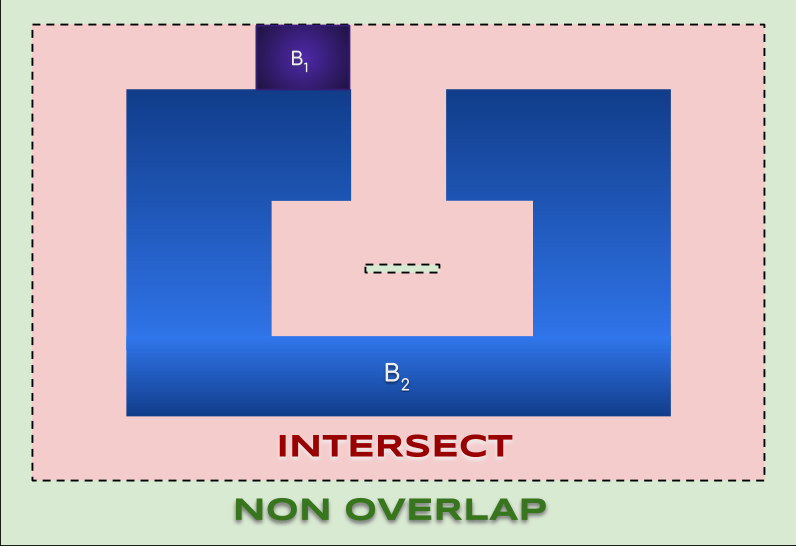
Les configurations en lesquelles $B_1$ est dans le col de $B_2$ sont dans TOUCH mais pas dans la frontière de INTERSECT.
\[\TOUCH = \NON ∩ \cl(\OVER)\]
Esquisse de preuve: Comme les objets sont égaux à l’adhérence de leur intérieur (pour $⊆$) - de même que les objets composés, puisque $\cl(\int(\bu))$ préseve l’union finie - et compacts (pour $⊇$), on montre que \(\underbrace{\left\lbrace x \mid ∃i≠ j. \overbrace{A_i}^{\llap{\text{objet composé}}}(x) ∩ \overbrace{A_j}^{\rlap{\text{objet composé}}}(x) ≠ ∅ \right\rbrace}_{\text{noté } \INTp \not ⊆ \VALID} = \cl\Bigg(\underbrace{\left\lbrace x \mid ∃i≠ j. \int(A_i(x)) ∩ \int(A_j(x)) ≠ ∅ \right\rbrace}_{\text{noté } \OVERp \not ⊆ \VALID}\Bigg)\)
Par fermeture de $\VALID$, il vient alors
\[\cl\Big(\underbrace{\OVER}_{≝\, \OVERp ∩ \VALID}\Big) = \cl(\OVERp) ∩ \VALID\]Et on conclut par \(\begin{align*} \TOUCH & = \OVERp^c ∩ \INTp ∩ \VALID\\ &= \OVERp^c ∩ \VALID ∩ \INTp ∩ \VALID\\ & = \underbrace{\OVERp^c ∩ \VALID}_{ = (\OVERp ∪ \VALID)^c ∩ \VALID \, =\, \NON} ∩ \cl(\OVER) \\ & = \NON ∩ \cl(\OVER) \end{align*}\)
Puis, comme $\BASE ∩ \NON ⊆ \TOUCH$:
\[\TOUCH = \FILL ∩ \cl(\OVER)\]
Connexité et contractilité
On montre le lemme suivant :
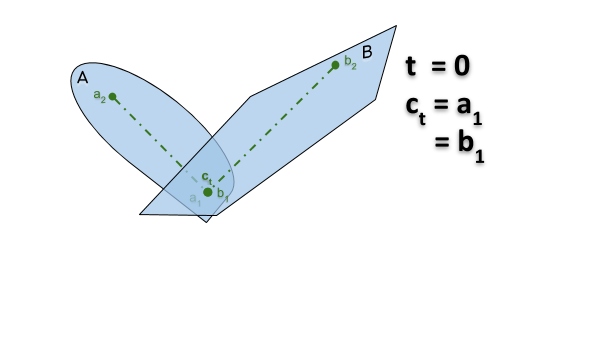
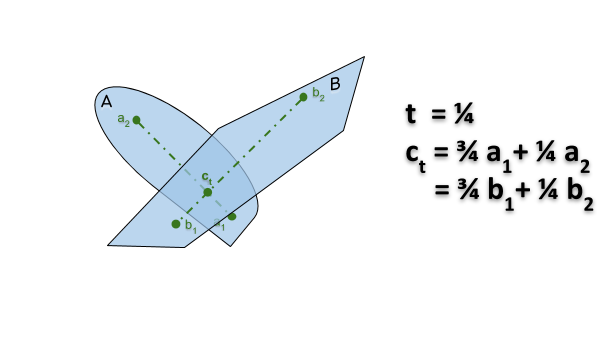
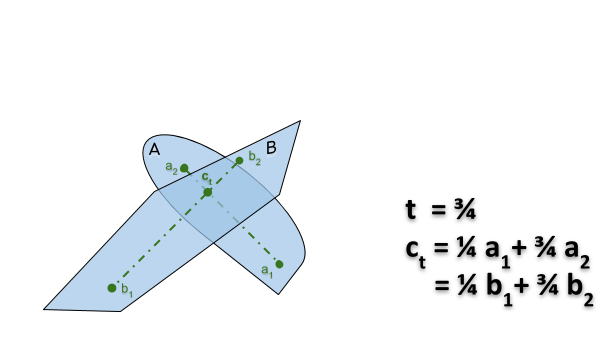
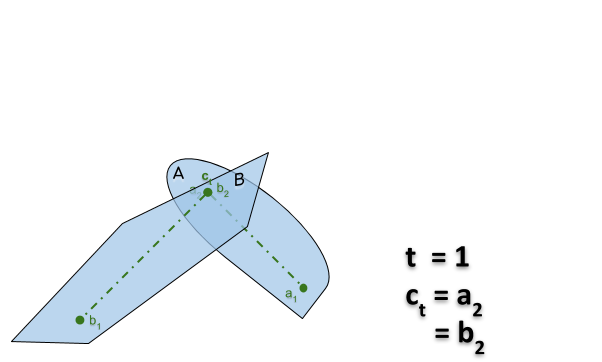
Si $A$ et $B$ sont des objets qui coïncident
- en $A \ni a_1 = b_1 ∈ B$ dans la configuration $x$
- en $A \ni a_2 = b_2 ∈ B$ dans la configuration $y$
alors il existe une translation de $A$ et $B$ entre $x$ et $y$ au cours de laquelle ils continuent de s’intersecter.
Preuve: On translate de telle sorte que le point $c_t = a_1 + (a_2-a_1)t = b_1 + (b_2-b_1)t$ reste un point d’intersection en $A$ et $B$ (voir le gif animé ici).
Avec le lemme précédent et des mouvements de rotation, on démontre que
BASE et FILL sont connexes par arcs
ainsi que le lemme suivant :
Lemme : De toute configuration dans VALID (resp. BASE), il existe un chemin dans VALID (resp. BASE) vers une configuration dans BASE où les origines des objets composés coïncident.
pour enfin conclure que
Corollaire : \(\FILL ∪ \NON = \BASE ∪ \VALID\) est contractile (et donc connexe par arcs)
Mayer-Vietoris
Intuitivement:
- l’homologie correspond à l’ensemble des invariants topologiques de $X$, indiqués par des groupes d’homologie
-
le $k$-ième groupe d’homologie $H_{k}(X)$ a autant de copies de $ℤ$ que $X$ contient de “trous” de dimension $k$. On utilisera donc le fait que :
- $H_0(X) ≃ ℤ^m$ si et seulement si $X$ a $m$ composantes connexes
- Si $X$ est contractile, alors $H_1(X) ≃ \lbrace 0 \rbrace$ (il ne peut pas y avoir de “trous”, par contractilité)
Mayer-Vietoris: La suite suivante est exacte:
\[\begin{align*} H_1(\FILL ∪ \NON) & {\xrightarrow {\partial _{*}}}\,H_0(\overbrace{\FILL ∩ \NON}^{=\, \TOUCH})\\ & {\xrightarrow {(i_{*},j_{*})}}\,H_0(\FILL)\oplus H_0(\NON) \\ & {\xrightarrow {k_{*}-l_{*}}}\,H_0(\FILL ∪ \NON) \\ & {\xrightarrow {\partial _{*}}}\, \lbrace 0 \rbrace \end{align*}\]
où $i, j, k, l$ sont les inclusions, et $\partial _{*}$ est défini à partir de l’opérateur bord.
Or, ici :
- $H_1(\FILL ∪ \NON) = \lbrace 0 \rbrace$ par contractilité
- $H_0(\FILL) = H_0(\FILL ∪ \NON) = ℤ$ par connexité par arcs
La suite suivante est donc une suite exacte courte :
\[\lbrace 0 \rbrace ⟶ \,H_0(\TOUCH) \,{\xrightarrow {(i_{*},j_{*})}} \, ℤ \oplus H_0(\NON) {\xrightarrow {k_{*}-l_{*}}}\, ℤ ⟶ \, \lbrace 0 \rbrace\]Et par injectivité de $(i_{*},j_{*})$ et surjectivité de $k_{*}-l_{*}$:
\[\Big(ℤ\oplus H_0(\NON)\Big)/\underbrace{\Im (i_{*},j_{*})}_{≃ \,H_0(\TOUCH)} ≃ ℤ\] \[⟹ H_0(\NON) ≃ H_0(\TOUCH)\]C’est-à-dire que $\NON$ et $\TOUCH$ ont le même nombre de composantes connexes !
Puis, le principe des tiroirs nous permet de conclure, après avoir montré que chaque composante connexe de $\NON$ contient une et une seule composante connexe de $\TOUCH$. En effet:
-
chaque composante connexe $t$ de $\TOUCH$ intersecte au plus une composante connexe de $\NON$, car sinon, si deux composantes $n_1, n_2 ⊆ \NON$ étaient intersectées par $t$: tout $x_1 ∈ n_1$ serait relié à tout $x_2 ∈ n_2$ par un chemin continu allant de $x_1$ à $t_1 ∈ t ∩ n_1 ≠ ∅$ (par connexité de $n_1$), puis de $t_1$ à $t_2 ∈ t ∩ n_2 ≠ ∅$ (connexité de $t$), et enfin de $t_2$ à $x_2$ (connexité de $n_2$).
-
chaque composante connexe $n$ de $\NON$ contient au moins une composante connexe de $\TOUCH$, car en translatant linéairement l’origine d’un objet $A_1$ vers celle d’un objet $A_2$ (et en notant $m(t)$ cette translation), les objets se touchent à l’instant \(t_0 ≝ \min_t \Big\lbrace m(t) \mid \begin{align*} &\quad m(t) ∉ \NON \backslash \TOUCH\\ ⟺ &\quad m(t) ∈ \OVER ∪ \TOUCH \end{align*}\Big\rbrace\)
Conclusion
On a montré que si
- il existe un chemin d’une configuration $x ∈ \TOUCH$ à $y ∈ \TOUCH$ dans $\NON$
- i.e $x ∈ \TOUCH$ et $y ∈ \TOUCH$ appartiennent à la même composante connexe $n ⊆ \NON$
alors
- en notant $t$ l’unique composante connexe de $\TOUCH$ qui intersecte $n$, nécessairement $x ∈ \TOUCH$ et $y ∈ \TOUCH$ appartiennent à $t$
- i.e $x$ et $y$ appartiennent une même composante connexe $\TOUCH \supset t ⊆ n$
- i.e. il existe un chemin de $x$ à $y$ dans $\TOUCH$
Enfin, on acquiert le résultat voulu en montrant, par induction sur le nombre $n$ d’objets composés, que : si il existe mouvement à $k+1$ composantes connexes (i.e à tout instant, il y a au plus $k+1$ composantes connexes) entre deux configuration à $k$ composantes connexes, alors il existe un mouvement à $k$ composantes connexes entre ces deux configurations (pour $1 ≤ k <n-1$).
Leave a comment