Cours 5 : Sémantique
Sémantique
Ex :
Sémantique de C :
Projet CompCert :
Deux grands styles de sémantique :
- Sémantiques opérationnelles :
- un programme = un gigantesque automate / graphe, dont les sommets sont les configuration
- ex: pour un ordinateur de $4GB$ de RAM, il y a environ $2^{32.10^9}$ de configurations : beaucoup trop énorme pour représenter le graphe dans l’univers physique
- un programme = un gigantesque automate / graphe, dont les sommets sont les configuration
⟶ on s’autorise des graphes dont les sommets sont des configurations en nombre infini dénombrable.
De plus : on définit une relation binaire notée $⟶$ :
\[C ⟶ C'\]transition de la configuration $C$ vers $C’$
Attention : “relation”, et pas “fonction”, car le graphe n’est pas forcément déterministe.
ex concret : on lit des sockets ⟶ on ne peut pas prédire ce qui sera stocké dans la chaîne (on ne sait ce qu’on va recevoir, à part si on a modélisé tout les univers possibles : pas faisable)
- Sémantiques dénotationnelles : les plus anciennes
Pour
- une expression $e$, on décrit sa valeur $⟦e⟧$
- une commande $c$, on décrit sa valeur $⟦c⟧$
NB : opérateur $⟦⟧$ : sémantique des valeurs
- Environnement :
- \[𝜌 ≝ \begin{cases} Var ⟶ ℤ \\ x \mapsto 𝜌(x) \end{cases}\]
NB : c’est du pipeau
Sémantique d’une commande :
on veut l’environnement à la fin de la commande.
- $𝜌[x \mapsto v]$ :
-
c’est la fonction qui :
- à $x$ associe $v$
- à tout $y≠x$ associe $𝜌(y)$
expression / environnements vers les environnements
OU
commandes / environnements vers les environnements
NB :
En logique : “frame problem” : on est obligé de préciser systématiquement “$y$ n’a pas changé” ⟶ alourdit les preuve
MAIS : produit de séparation résout ça
\[⟦while 1 do skip⟧𝜌 ≝ ⟦while 1 do skip⟧(⟦skip⟧𝜌) = ⟦while 1 do skip⟧(𝜌)\]Gros problème :
while: par bien fondé !
Comment on résout ce problème ? avec un théorème de point fixe fonctionnel.
Sémantique 0 (opérationnelle, petits pas)
Une configuration est :
- un couple $(c,𝜌)$ d’une commande et d’un environnement
- OU : $𝜌$ (si on a terminé l’exécution)
NB :
en fait,
- commandes $c_i ≡$ intervalles
- environnements $𝜌 ≡$ poteaux
NB :
aucun problème définitionnel, pour les sémantiques opérationnelles : ensemble de règles
Sémantique 1 (opérationnelle, petits pas)
Une configuration est :
- un couple $(C,𝜌)$ d’une liste de commandes et d’un environnement
- NB : $(𝜀, 𝜌)$ est une configuration sans successeur : phénomène de terminaison
- OU : $(𝜀, 𝜌)$ (si on a terminé l’exécution)
Deadlock : en programmation parallèle, on a deux threads qui manipulent une même variable $x$.
Pour éviter ça : systèmes de synchronisation :
- ex: les sémaphores de Djikstra : $P$, $V$ (en hollandais : “essayer d’acquérir, libérer”)
- il n’y a pas deux processus qui peuvent acquérir le même sémaphore en même temps
Contrat : n’utiliser $x$ que quand j’ai le sémaphore, puis je le passe aux autres.
Mais problème : 2 processus se battent pour deux sémaphores :
- le premier veut $A$, puis $B$
- le deuxième veut $B$, puis $A$
chacun des deux veut acquérir le sémaphore de l’autre et attend que l’autre le lâche : il reste des trucs à faire, mais bloqué ⟶ deadlock.
Sémantique opérationnelle à grands pas
Plutôt que décrire l’exécution étape par étape élémentaires, ça nous décrit directement comment passer de la configuration initiale à la configuration finale.
NB : ne parle QUE des programmes qui temrminent.
C’est même une caractérisation : un programme termine ssi il existe une dérivation pour ce programme
Ce qu’on prétend :
les sémantiques opérationnelles à petit pas et grand pas font la même chose.
Si
\[(C, 𝜌) ⟶^\ast (𝜀, 𝜌)\]alors
\[𝜌 \vdash C^; ⟹ 𝜌_∞\]NB : attention, $C$ est une liste de commandes, alors que $C^;$ est une commande ⟶ on “convertit” tous les “$\cdot$” en “$;$”, avec
- $𝜀^; = skip$
- $(c \cdot C)^; = c; C^;$
HS : Lemme de Yoneda
Proposition :
Si $(C_1, ρ_1) → (C_2, ρ_2)$ dans la sémantique à petits pas, alors :
Pour tout environnement $ρ_∞$ tel que $ρ_2 ⊢ C_2^; ⇒ ρ_∞$ est dérivable en sémantique à grands pas, $ρ_1 ⊢ C_1^; ⇒ ρ_∞$ est aussi dérivable en sémantique à grands pas.
Adéquation :
Utiliser un lemme intermédiaire :
\[∀C, (c \cdot C, 𝜌) ⟶^\ast (C, 𝜌_∞)\]Par ex, pour (Seq) :
\[((c_1; c_2) \cdot C, 𝜌) ⟶ (c_1 \cdot \underbrace{c_2 \cdot C}_{≝ C'}) ⟶^\ast (C', 𝜌') ⟶^\ast (C, 𝜌'')\]Optimisations d’un compilateur : se font par des techniques d’analyse statique basées sur les sémantiques.
Unique point pénible : assurer la terminaison.
Retour sur la sémantique dénotationelle
\[⟦x:=e⟧𝜌 = 𝜌[x \mapsto ⟦e⟧𝜌] \\ ⟦skip⟧𝜌 = 𝜌 \\ ⟦while \, \, e \, \, do \, \, c⟧𝜌 = \begin{cases} ⟦while \, \, e \, \, do \, \, c⟧(⟦c⟧𝜌) \text{ si } ⟦e⟧𝜌 ≠ 0 \\ 𝜌 \end{cases}\]On a vu que $⟦while \, \, e \, \, do \, \, c⟧𝜌$ n’est pas bien fondé, en fait : en cas d’existence, c’est un point fixe de la fonction :
\[F : f \mapsto \begin{cases} f(⟦c⟧𝜌) \text{ si } ⟦e⟧𝜌 ≠ 0 \\ 𝜌 \end{cases}\]Treillis
- Treillis :
-
Ensemble ordonné dans lequel toute paire (d’éléments) admet une borne sup et une borne inf. (cf. diagramme de Hasse qd $x,y$ non comparables).
- Treillis complet :
-
Si, de plus, pour toute partie $F ⊆ E$, $F$ admet un borne sup et une borne inf.
Supposer que l’existence d’une borne sup suffit : l’existence d’une borne inf est un théorème.
Dém :
Considérons le sup $a_0$ de l’ensemble $A$ des minorants d’une partie $B$.
Si $a_0 ∈ A$, $a_0$ est une borne inf de $B$.
Montrons que c’est le cas : pour tout $b∈B$, mq $a_0 ≤ b$, i.e $∀a∈A, a ≤ b$.
Si $a∈A$, $a ≤ b$ est bien, par définition de $A$ (ensemble des minorants de $B$).
NB : Un treillis complet a un plus grand (resp. petit) élément, puisque $E ⊆ E$ a une borne sup (qui lui appartient ⟶ plus grand élément).
Ex:
1) $(ℕ\backslash{0}, \vert )$ est un treillis (non complet, car seules les parties finies admettent une borne sup a priori (l’ensemble $ℙ$ n’a pas de majorant)).
2) $(𝒫(X), ⊆)$ est un treillis complet :
- Borne sup de $S⊆𝒫(X)$ = $\bigcup_{Y∈S} Y$
- Borne inf de $S⊆𝒫(X)$ = $\bigcap_{Y∈S} Y$
3) Pour une topologie, l’ensemble des ouverts est un treillis complet (l’union d’ouverts reste un ouvert (borne sup)).
L’inf d’une famille d’ouverts, c’est l’intérieur de l’intersection.
- Point fixe d’une applcation $f: E ⟶ E$ :
-
Un élément $x$ tq $f(x)=x$
Th de Knaster-Tarski : Soit $(E,≤)$ un treillis complet, $f: E ⟶ E$ monotone.
Alors $f$ admet un plus petit pt fixe, et un plus grand pt fixe.
NB :
- fonction “monotone” : c’est un anglicisme (pour dire “croissante”).
- en fait, on a même mieux : l’ensemble des points fixes est un treillis complet.
-
Heuristique :
- $(f^n(\bot))_n$ est une suite croissante.
- si en on note $f^𝜔(\bot)$ le sup : on a $f^𝜔(\bot) ≤f^{𝜔+1}(\bot)$
- puis, avec les ordinaux : $f^{𝜔^k}(\bot) ≤f^{𝜔^{k+1}}(\bot)$
- particularité des ordinaux : le sup d’une famille est un ordinal
- puis : paradoxe de Burali-Forti
- l’ensemble de tous les ordinaux est un ordinal : bizarre car cet ordinal est alors strictement plus grand que lui-même (à la Russel)
- en fait : il n’y a pas d’ensemble des ordinaux.
- donc ici : comme on a bien a affaire à un ensemble, on ne peut pas avoir stricte croissance de la suite précédente ⟶ il y a un point fixe.
Dém :
On pose $F≝ \lbrace x∈E; x\leq f(x)\rbrace$
NB : un $x$ tel que $x≤f(x)$ s’appelle un post-point fixe (même déf pour “pré-point fixe”)
On remarque que $\bot ∈ F$, donc $F \neq ∅$.
Comme $(E,≤)$ est un treillis complet, $F$ admet une borne sup $y$.
Mq $y∈F$ :
Soit $x∈F$ : $x≤y$, et donc ($f$ monotone) $f(x)≤f(y)$.
Ainsi \(x ≤ f(x) ≤ f(y)\)
Donc $f(y)$ majore $F$, et donc \(y ≤ f(y)\) ($y$ : + petit des majorants de $F$), donc $y ∈ F$ (déf de $F$).
Par monotonie de $f$ : $f(F)⊆F$.
Donc $f(y) ∈ F$, et donc $f(y) ≤ y$, d’où \(y = f(y)\)
Comme $F$ contient tous les pts fixes de $f$, alors $y$ est le plus grand point fixe de $f$.
(dém analogue pour la borne inf)
Application : Th de Cantor-Bernstein
Dém :
Soient $E, F$ deux ensembles, $f: E⟶F$ et $g: F⟶E$ injectives.
On pose \(H ≝ \begin{cases} 𝒫(E) ⟶ 𝒫(E) \\ X \mapsto E\backslash g(F\backslash f(X)) \end{cases}\)
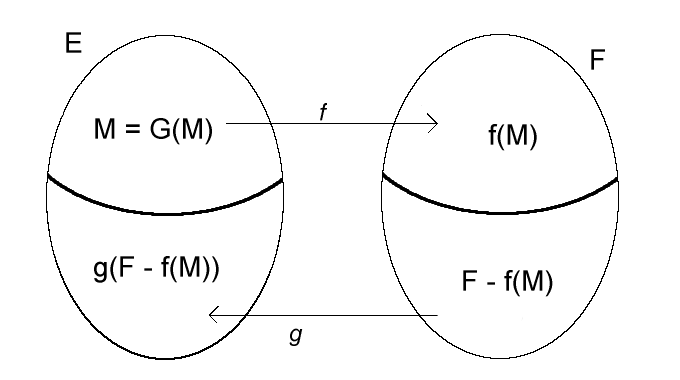
($H = G$ sur ce dessin)
1) Mq $H$ est monotone.
Soient $X, Y ⊆ E$ tq $X⊆Y$.
\[\begin{align*} X⊆Y &⟹ f(X) ⊆ f(Y) \\ &⟹ F\backslash f(Y) ⊆ F\backslash f(X) \\ &⟹ g(F\backslash f(Y)) ⊆ g(F\backslash f(X)) \\ &⟹ H(X) = E\backslash g(F\backslash f(X)) ⊆ H(Y) = E\backslash g(F\backslash f(Y)) \end{align*}\]Par le th de Knaster-Tarski, $H$ admet un point fixe $Z$.
\[Z = H(Z) = E\backslash g(F\backslash f(Z)) \\ ⟹ E\backslash Z = g(F\backslash f(Z))\]On définit \(h ≝ \begin{cases} E ⟶ F \\ x \mapsto \begin{cases} f(x) \text{ si } x∈Z \\ g^{-1}(x) \text{ sinon. } \end{cases} \end{cases}\)
NB : Comme $E\backslash Z = g(F\backslash f(Z))$, si $x \not ∈ Z$, $∃u ∈ F\backslash f(Z); x = g(u)$, et $u$ est unique par injectivité de $g$.
Mq $h$ est injective :
Si $x,y ∈E; h(x) = h(y)$.
- Si $x, y∈Z$ : $x=y$ par injectivité de $f$
- Si $x, y\not∈Z$ : $x,y$ ont le même antécédent par $g$, donc $x=y$
- Si $x∈Z, y\not∈Z$ : $h(x) = f(x) ∈ f(Z)$, $h(y) = g^{-1}(y) ∈ F\backslash f(Z)$, donc $h(x) \neq h(y)$.
Mq $h$ est surjective :
Soit $y ∈ F$.
- Si $y ∈ f(Z), ∃ z ∈ Z; y = f(z)$, et $y = f(z) = h(z)$
- Si $y \not∈ f(Z), y = g^{-1}(g(y)) = h(g(y))$
Langages algébriques
Langages reconnus par automates à piles.
Ex :
Grammaire :
- $S ⟶ 𝜀$
- $aSb$
⟹ Langage ${a^n b^n, n ∈ ℕ}$
$f({\cal L}) = {\cal L} ∪ a {\cal L} b$
${a^n b^n, n ∈ ℕ}$ est le plus petit point fixe de $f$.
- Directed Complete Partial Order (DCPO) :
-
Un ensemble partiellement ordonné tel que toutes les familles dirigées aient des bornes sup.
- Famille dirigée $(x_i)_{i∈I}$ d’élément de $X$ :
-
- famille non vide
- telle que : $∀i, j, ∃ k; x_i, x_j ≤ x_k$
graph mon_graphe {
rankdir=BT;
x_i -- x_k;
x_j -- x_k;
}
Exs de DCPO :
- tout treilis complet
-
L’ensemble de Scott
\[\{[a,b] \vert \, \, a, b ∈ ℝ, a≤b\}\]muni de l’ordre $\supseteq$
NB : ça n’est pas un treillis complet, à cause de l’ensemble vide.
- $f : X ⟶ Y$ est Scott-continue ssi :
-
- $f$ monotone
- $∀(x_i)_{i∈I}$ dirigée dans $X$, \(\sup_{i∈I} f(x_i) = f(\sup_{i∈I} x_i)\)
Notation : L’ensemble des fonctions Scott-continues de $X$ ) $Y$ est noté \([X ⟶ Y]\)
NB :
- ça coïncide bien avec la continuité pour la topologie de Scott.
- la famille $(f(x_i))_i$ est dirigée, d’où l’existence du sup
-
pour vérifier cette égalité, on procède par double inégalité, sachant que $\sup_{i∈I} f(x_i) ≤ f(\sup_{i∈I} x_i)$ est toujours vraie
- seule chose à démontrer, sachant que $f$ monotone : $\sup_{i∈I} f(x_i) ≥ f(\sup_{i∈I} x_i)$
Th de Kleene : Soit $X$ un dcpo pointé (i.e avec un plus petit élément $\bot$).
Toute fonction Scott-continue $f: X ⟶ X$ a un plus point fixe :
\[lfp(f) ≝ \sup_{n∈ℕ} f^n(\bot)\]
$(f^n(\bot))_n$ est une chaîne, donc dirigée.
Posons
\[x = \sup_n f^n(\bot)\]Alors :
\[f(x) = f(\sup_n f^n(\bot)) \\ = \sup_n f^{n+1}(\bot)\](par Scott-continuité)
Donc :
\(x = f(x)\) et $x$ est un point fixe.
Montrons que c’est le plus petit :
Si $y$ est un autre point fixe :
\[\bot ≤ y \\ ⟹ f(\bot) ≤ f(y)=y \\ ⟹ ∀n, f^n(\bot) ≤ y \\ ⟹ x ≤ y\]($x$ est le sup = le plus petit des majorants) ___
Fait : Si $X$ et $Y$ sont des DCPO, alors $X\times Y$ reste un DCPO
où : $(x, y) ≤ (x’, y’) ⟺ (x ≤_X x’ ∧ y ≤_Y y’)$
NB : Selon Gordon Plotkin : en théorie des domaines, soit
- ça foire lamentablement
- ça réussit magnifiquement
Preuve :
Soit \(((x_i, y_i))_{i∈I}\) une famille dirigée.
Montrons que son sup est
\[(x,y) ≝ (\sup_i x_i, \sup_j y_j)\]lequel existe car :
-
$(x_i)_i$, $(y_i)_i$ sont dirigées
- projeter sur la première composante le majorant exhibé par la définition de “$((x_i, y_i))_{i∈I}$ est une famille dirigée”
- $(x,y)$ est un majorant : par déf
-
c’est le plus petit :
- Si $∀i∈I, (x’, y’) ≥ (x_i, y_i)$, alors $∀i, x’ ≥ x_i$ et $∀i, y’ ≥ y_i$.
- Donc $x’ ≥ \sup_i x_i$ et $y’ ≥ \sup_i y_i$.
- Donc $(x’, y’) ≥ (\sup x_i, \sup y_i) = (x, y)$
Proposition : Si $X$ et $Y$ sont des DCPO, l’ensemble des fonctions Scott-continues $[X⟶Y]$ est un DCPO :
- $f ≤_{[X⟶Y]} g$ ssi $∀x∈X, f(x) ≤_Y g(x)$
- Pour toute famille dirigée $(f_i)_{i∈I}$ :
- $(\sup_i f_i)(x) = \sup_i(f_i(x))$
Dém :
Se déroule naturellement :
- bonne définition : évidente en montrant que $(f_i(x))_i$ est dirigée
- monotonie de $f$ : caractérisation du sup
- Scott-continuité de $f$ : en utilisant le fait que $\sup_i \sup_j = \sup_j \sup_i$ (on fait commuter les quantificateurs universels)
- $f$ est un majorant des $f_i$ : en utilisant $∀x, ∀i = ∀i, ∀x$
- $f$ est plus petite que tout majorant $g$ des $f_i$ : en utilisant $∀x, ∀i = ∀i, ∀x$
Propriété : L’application
\[App : \begin{cases} [X⟶Y]\times X ⟶ Y \\ (f,x) \mapsto f(x) \end{cases}\]
Dém :
- $App$ monotone
- Soit $(f_i, x_i)_i$ dirigée dans $[X⟶Y]\times X$.
On va avoir un problème : quantification sur $i$ et $j$ d’un côté, quantification que sur $k$ de l’autre.
Il y a une inégalité claire.
L’autre vient du fait que la famille de couples considérée est dirigée.
NB : en topologie :
- notion de continuité séparément et de continuité conjointement
- Normalement : elles ne coïncident pas du tout (reprendre les exemples classiques d’analyse)
-
Mais ici, dans les DCPO avec la topologie de Scott : continuité séparément = continuité conjointement, ce qui est un miracle !
- c’est pour ça que tout va marcher, en sémantique !
- la catégorie des CPO avec la topologie de Scott est cartésienne close !
- Lifting du DCPO $X$, noté $X_\bot$ :
-
c’est $X$ muni d’un minimum $\bot$, et ça reste un DCPO.
- DCPO obtenu à partir d’un ensemble $E$ :
-
c’est le DCPO $(E, =)$
- DCPO plat :
-
c’est un DCPO de la forme $(E_\bot, =)$, où $E$ est un ensemble.
Retour à la sémantique dénotationnelle
\[⟦while \, \, e \, \, do \, \, c⟧𝜌 = \begin{cases} 𝜌 \text{ si } ⟦e⟧𝜌 = 0 \\ \bot \text{ si } ⟦e⟧𝜌 ≠ 0 ∧ ⟦c⟧𝜌 = \bot \\ ⟦while \, \, e \, \, do \, \, c⟧(⟦c⟧𝜌) \text{ si } ⟦e⟧𝜌 ≠ 0 ∧ ⟦c⟧𝜌 ≠ \bot \\ \end{cases}\]Donc en posant $f ≝ ⟦while \, \, e \, \, do \, \, c⟧$ :
\[f : 𝜌 \mapsto F_{e,c}(f) ≝ \begin{cases} 𝜌 \text{ si } ⟦e⟧𝜌 = 0 \\ \bot \text{ si } ⟦e⟧𝜌 ≠ 0 ∧ ⟦c⟧𝜌 = \bot \\ f(⟦c⟧𝜌) \text{ si } ⟦e⟧𝜌 ≠ 0 ∧ ⟦c⟧𝜌 ≠ \bot \\ \end{cases}\]Donc on pose :
\[⟦while \, \, e \, \, do \, \, c⟧ = lfp(F_{e,c})\]On se place dans le DCPO $[Env ⟶ Env_\bot]$ (on n’a pas à se préoccuper de la continuité des fonctions : elles sont toutes continues dans $Env ⟶ Env_\bot$ (DCPO plat)).
NB :
il faut montrer que la fonction $F_{e,c}$ est Scott-continue.
- en utilisant la cloture par composition des fonctions Scott-continues, et la continuité de la fonction $App$.
Miracle : en choisissant le plus petit point fixe, on va montrer l’équivalence des sémantiques dénotationnelle et opérationnelles.
NB :
-
le théorème de correction n’utilise que le fait que c’est un point fixe.
Équivalence contextuelle
Morris : deux programmes sont équivalents ssi on ne voit pas la différence : à toute entrée, ils donnent la même sortie.
Programme équivalents ⟺ ont le même comportement (i.e on observe les mêmes effets) dans le même contexte.
Mais dans notre cas : on prendra un critère beaucoup plus faible :
-
même comportement =
- terminent sur les mêmes entrées
- donnent zéro dans sur les mêmes entrées
⟶ mais par une réduction (en considérant les contextes qui plantent quand 0 est renvoyé), cela revient au même
Th \((c, 𝜌) ≃ (c', 𝜌') ⟺ ⟦c⟧𝜌 = ⟦c'⟧𝜌'\)
- $⟸$ :
De la sémantique dénotationnelle de la séquence, on déduit :
\[⟦c⟧𝜌 = ⟦c'⟧𝜌' ⟹ ⟦c;C^;⟧𝜌 = ⟦c';C^;⟧𝜌'\]
Leave a comment