[Problem Set 2 Quantitative models of behavior] Problem 3: The drift diffusion model of decision-making

Link of the iPython notebook for the code

AT2 – Neuromodeling: Problem set #2 QUANTITATIVE MODELS OF BEHAVIOR

PROBLEM 3: The drift diffusion model of decision-making.

We consider a two-alternative forced choice task (2AFC-task): the subject (e.g. a monkey) sees a cluster of moving dots (in many directions) on a screen and is to choose (whenever he/she/it wants) whether they are moving upwards or downwards.

In the drift-diffusion-model, the subject is assumed to compare two firing rates:

  • one firing rate of an upward-motion sensitive neuron, denoted by $m_A$
  • and another one from a downward-motion sensitive neuron, denoted by $m_B$

Then, the subjects integrates the difference as follows:

\[\dot{x} = m_A − m_B + σ η(t)\]

where $η(t) \sim 𝒩(0, 1)$ is a Gaussian white noise.

For a given threshold $μ$:

  • if $x ≥ μ$ then the subject chooses $A$
  • else if $x ≤ -μ$ then the subject chooses $B$

We have the following discrete approximation of the drift-diffusion-model:

\[x(t+∆t) = x(t) + (m_A - m_B) ∆t + σ η(t) \sqrt{∆t}\]

1. Reaction times

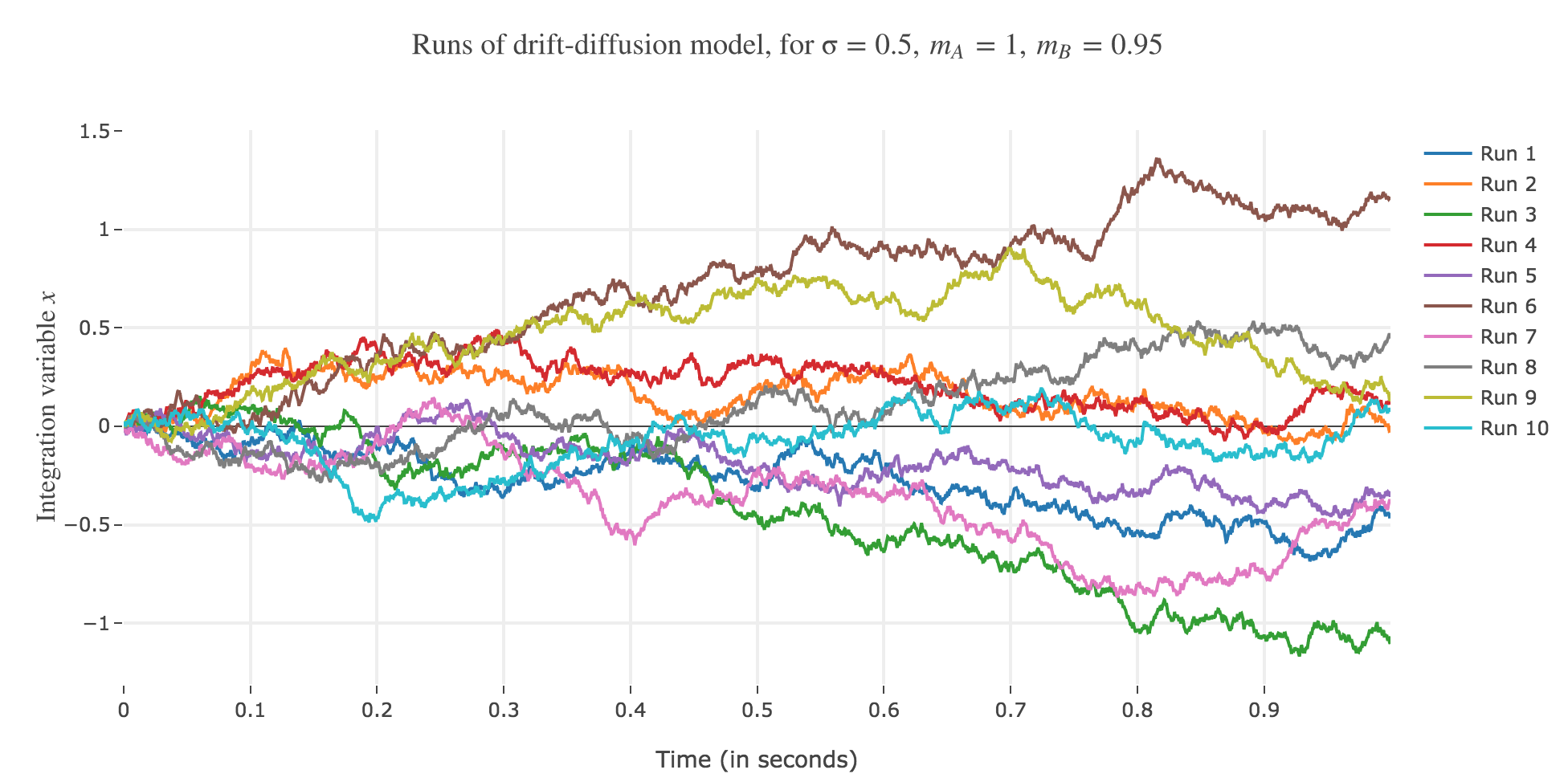
Let $m_A ≝ 1, m_B ≝ 0.95, \, σ ≝ 0.5, \, x(0) ≝ 0$, and $∆t ≝ 0.1 \, \mathrm{ ms}$.

Let us run the drift-diffusion-model ten times with the above parameters, with resort to the Euler method:

Figure 4.1.
Figure 3.1. - Ten runs of the drift-diffusion-model, with $m_A ≝ 1, m_B ≝ 0.95, \, σ ≝ 0.5, \, x(0) ≝ 0$

Now, after running the model $N$ times and storing the outcome and the time of threshold crossing (denoted by $t_i$) for each run: let us plot the distribution of reaction times for outcome $A$ and $B$, given that the reaction time is given by:

\[RT_i = 100 + t_i\]

  • For $N ≝ 1000$:

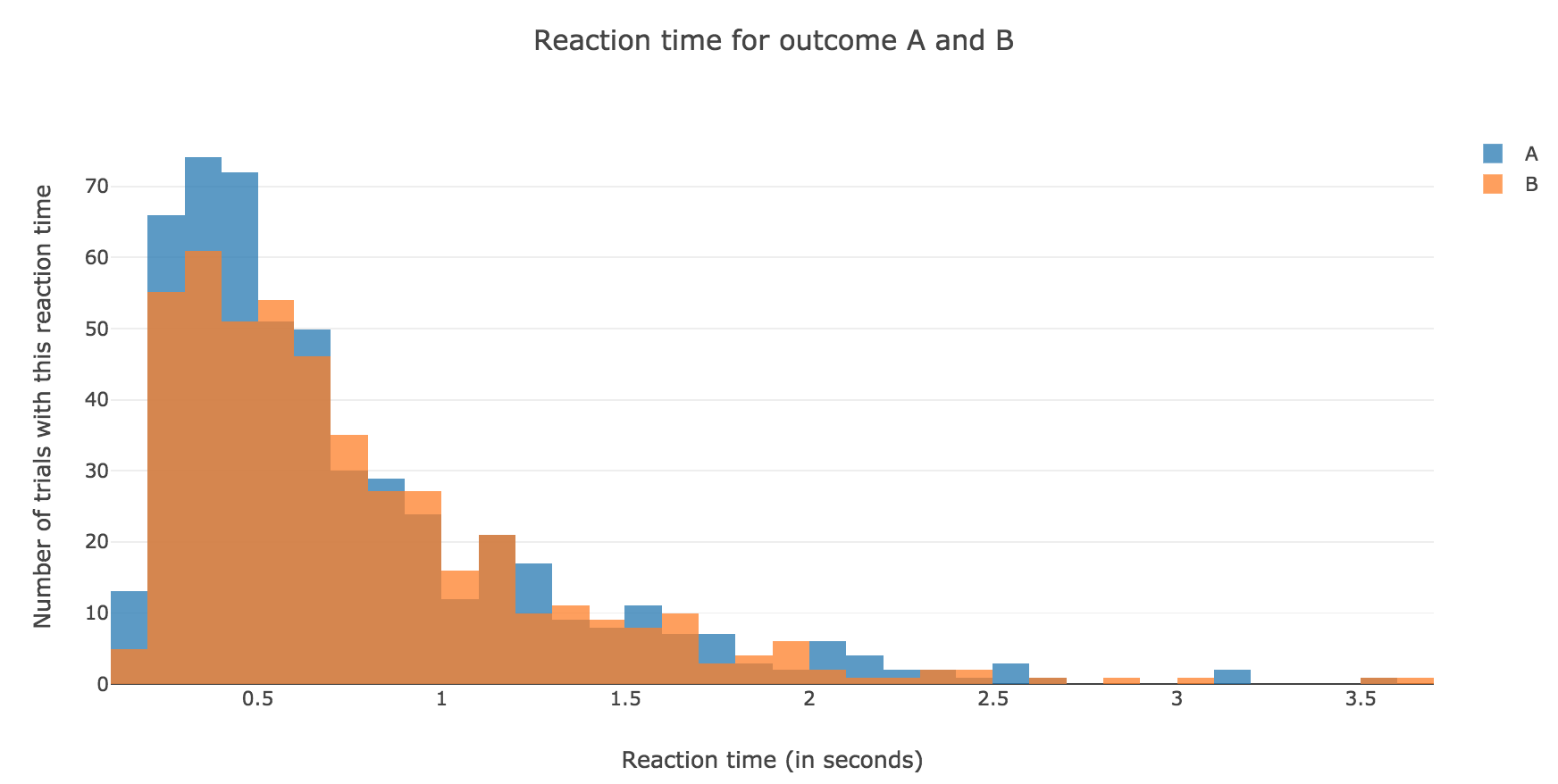
    Figure 1.1.
    Figure 1.1. - Distribution of reaction times for outcome $A$ and $B$ after running the model $N = 1000$ times

  • For $N ≝ 10000$:

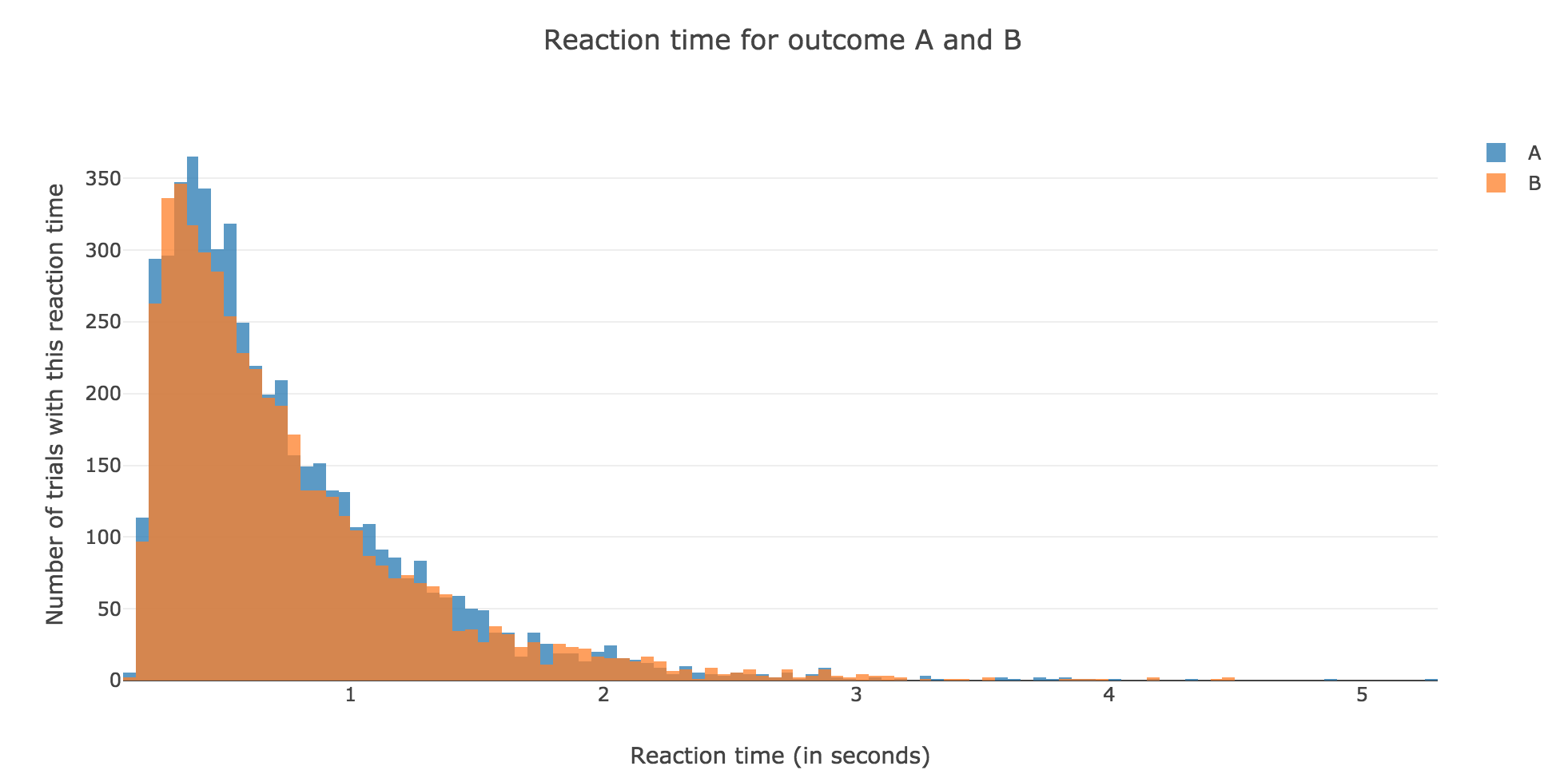
    Figure 1.2.
    Figure 1.2. - Distribution of reaction times for outcome $A$ and $B$ after running the model $N = 10000$ times

2. Probability of outcome $A$

Let us define the evidence for outcome $A$ versus outcome $B$ as:

\[m_E ≝ m_A - m_B\]

The analytical formula of the probability of outcome $A$ is:

\[p_A ≝ \frac{1}{1+ \exp(-β m_E)}\]

where $β ≝ \frac{2 μ}{σ^2}$.

Let us compare it, for values of $m_E$ ranging from $-0.2$ to $0.2$, with the empirical probability we can get from our simulation, by running the model $N$ times (for $N$ sufficiently large) and computing:

\[P(A) ≝ \frac{\text{Number of trials of outcome } A}{\text{Number of trials of outcome } A + \text{Number of trials of outcome } B}\]

The problem is that we have to compute this empirical probability for several values of $m_E$ ranging from $-0.2$ to $0.2$! As a matter of fact: the previous naive algorithm, based on the Euler method, is far too slow…

But we can cope with that with a trick!

Fast algorithm to compute the distribution of reaction times

From the discrete approximation of the drift-diffusion-model:

\[x(t+∆t) = x(t) + m_E ∆t + σ η(t) \sqrt{∆t}\]

So for all $n ≥ 1$:

\[x(t+ n ∆t) = x(0) + n \cdot m_E ∆t + σ \sqrt{∆t} \sum\limits_{ i=1 }^n η_i(t)\]

where the

\[η_i(t) \sim 𝒩(\overbrace{0}^{ ≝ \, μ_i}, \overbrace{1}^{≝ \, σ_i^2})\]

are independent and normally distributed random variables.

But it is well known that a sum of independent and normally distributed random variables is also a normally distributed variable, such that:

\[\sum\limits_{ i=1 }^n η_i(t) \sim 𝒩\left(\sum\limits_{ i=1 }^n μ_i \, , \; \sum\limits_{ i=1 }^n σ_i^2\right)\]

i.e.

\[\sum\limits_{ i=1 }^n η_i(t) \sim 𝒩(0, n)\]

But as it happens:

\[\sqrt{n} \underbrace{η(t)}_{\sim 𝒩(0, 1)} \sim 𝒩(0, n)\]

So for all $n ≥ 1$, we can set $x(t + n ∆t)$ to be:

\[x(t + n ∆t) = x(0) + n \cdot m_E ∆t + \sqrt{n} \cdot σ \sqrt{∆t} η(t)\]

where $η(t) \sim 𝒩(0, 1)$

So solving for $n$ in the threshold crossing conditions:

\[x(t + n ∆t) = ± μ\]

is tantamount to:

  • Analysis: solving (for $ξ$, in $ℂ$) two quadratic equations for a given $η(t) ∈ ℝ$:

    \[\begin{cases} m_E ∆t \, ξ^2 + σ \sqrt{∆t} η(t) \, ξ + x(0) - μ = 0&&\text{(outcome A)}\\ m_E ∆t \, ξ^2 + σ \sqrt{∆t} η(t) \, ξ + x(0) + μ = 0&&\text{(outcome A)}\\ \end{cases}\]

  • Synthesis: keeping only the roots $ξ$ such that $ξ^2 ∈ ℝ_+$, and setting $n ≝ \lceil ξ^2 \rceil$

which gives us a very fast algorithm!

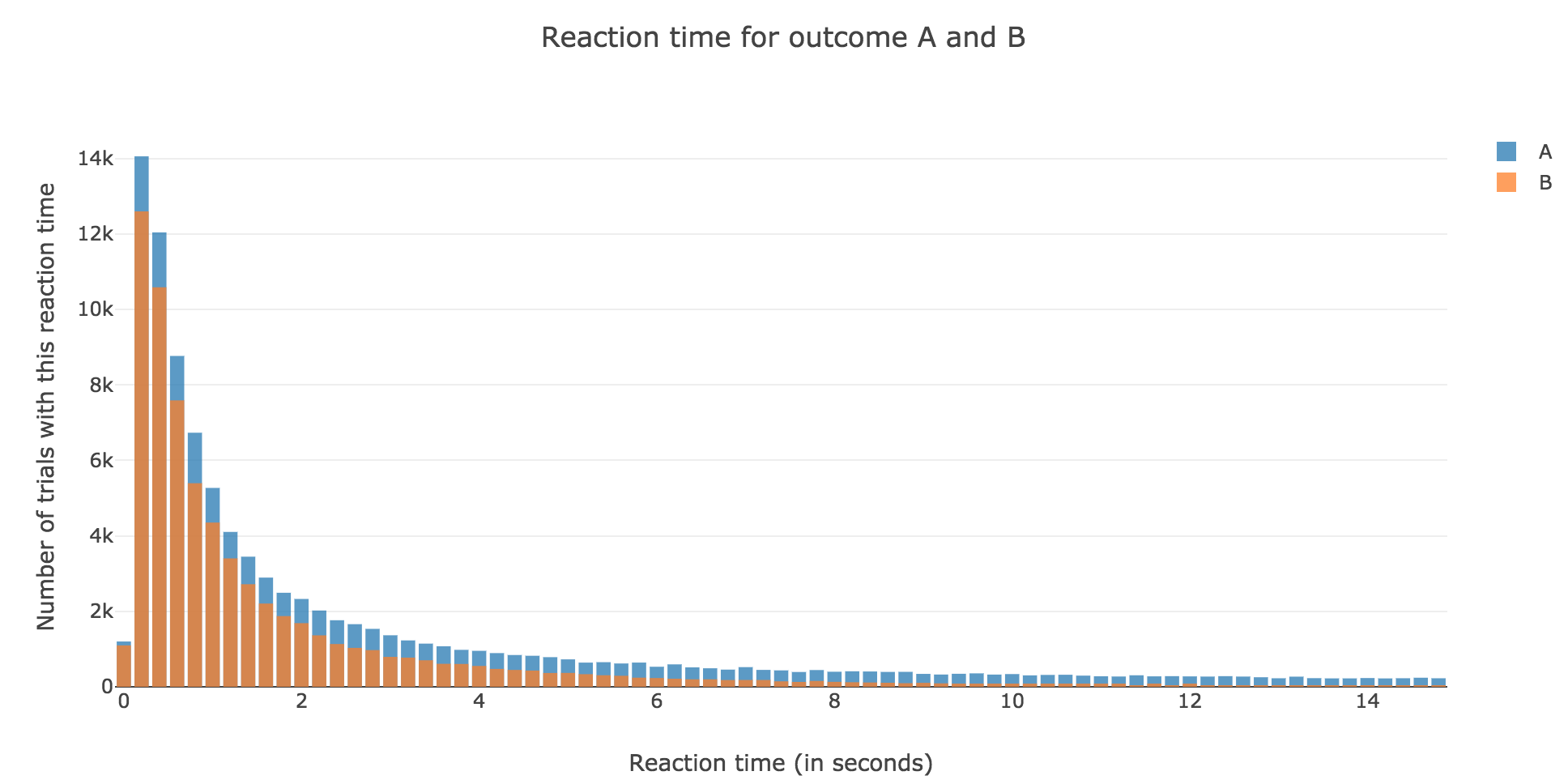
Figure 4.1.
Figure 2.1. - Distribution of reaction times for outcome $A$ and $B$ computed with the previous trick

Finally, we can compare the empirical probability of outcome $A$ with the analytical one:

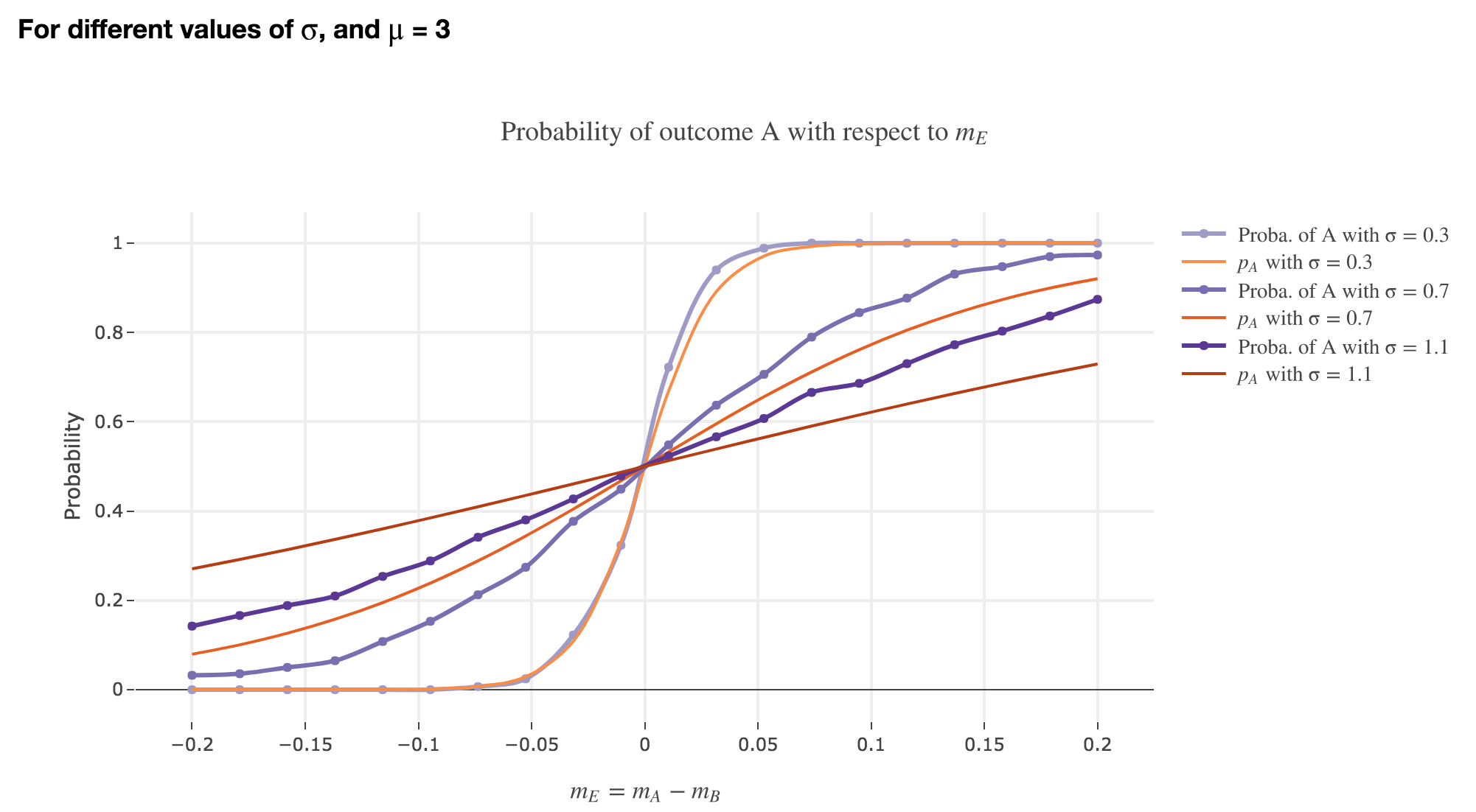
Figure 4.1.
Figure 2.2. - Comparison of the empirical probability of outcome $A$ with $p_A$ (as functions of $m_E$), for different values of $μ$
Figure 4.1.
Figure 2.3. - Comparison of the empirical probability of outcome $A$ with $p_A$ (as functions of $m_E$), for different values of $μ$

We see that the empirical probability of outcome $A$ matches more and more $p_A$ (when it comes to the shape of the curve):

  • as $μ$ increases

  • as $σ$ decreases (with an almost perfect match above for $σ = 0.3$)

Leave a comment