[Problem Set 2 Quantitative models of behavior] Problem 2: Decision strategy for flower sampling by bees
Link of the iPython notebook for the code
AT2 – Neuromodeling: Problem set #2 QUANTITATIVE MODELS OF BEHAVIOR
PROBLEM 2: Simple decision strategy for flower sampling by bees.
Let us consider the following experiment: a bee lands on flowers to collect as much nectar as possible, during two day (granting that it lands on $100$ flowers a day). There are two kinds of flowers:
-
blue flowers, which carry a nectar reward of
- $r_b = 8$ during the first day
- $r_b = 2$ during the second day
-
yellow flowers, which carry a nectar reward of
- $r_y = 2$ during the first day
- $r_y = 8$ during the second day
The bee’s internal estimate for the rewards is $m_b$ (resp. $m_y$) for the blue (resp. yellow) flowers. The bee chooses to land on a blue flower with probability (softmax-strategy):
\[p_b = \frac{1}{1 + \exp(β (m_y - m_b))}\]where $β$ is called the “exploitation-exploration trade-off” parameter (we will explain why in the following section).
1. The softmax-strategy
Note that $p_b$ is a sigmoid of $-(m_y - m_b)$ (for a fixed $β$) and a sigmoid of $-β$ (for a fixed $m_y - m_b$).
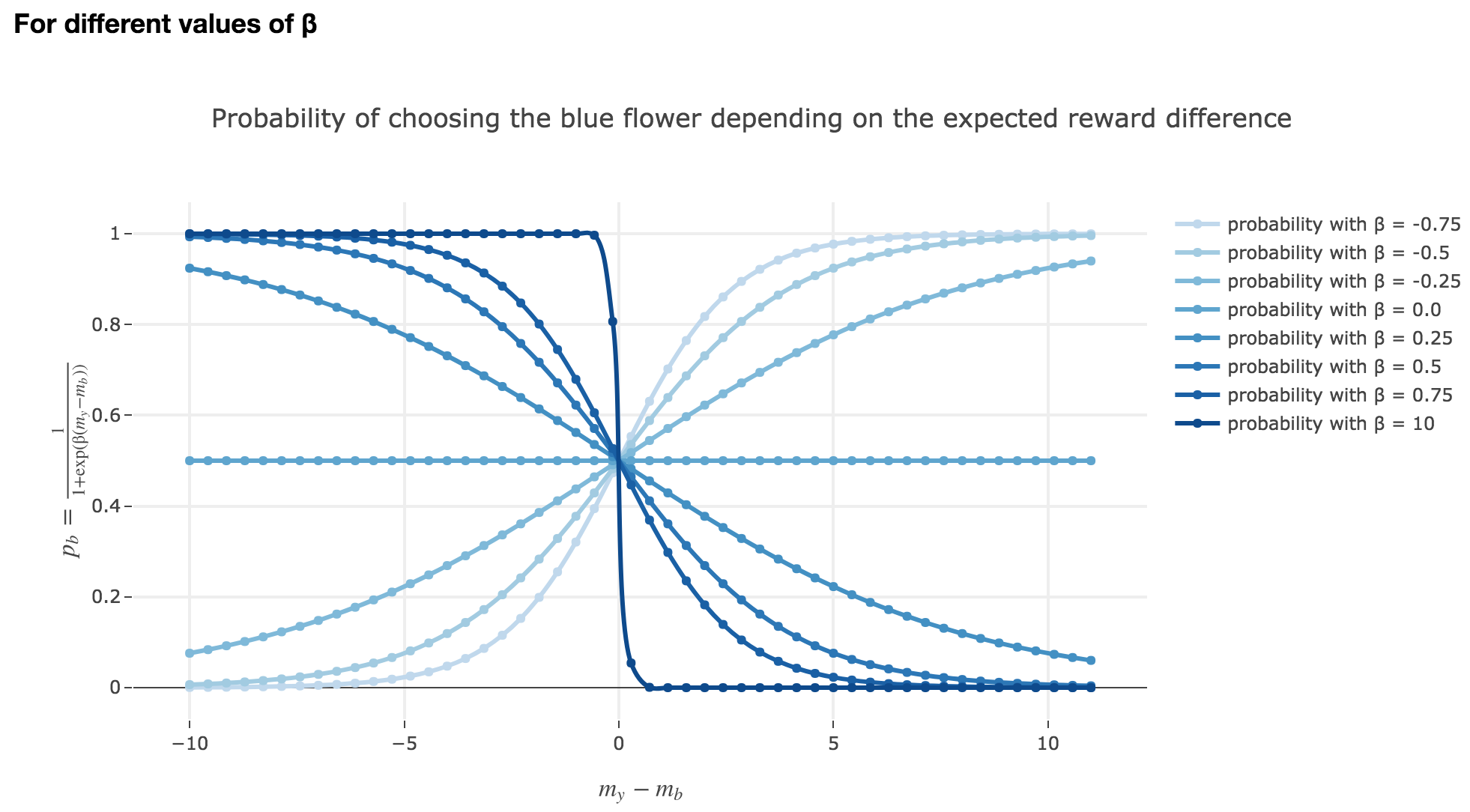
Thus:
-
the larger $m_y - m_b$, the higher the bee’s internal estimate of the yellow flower is compared to the blue one. As a consequence, the lower the probability $p_b$ of the bee landing on the blue one.
-
the lower the reward difference, the worse the bee considers the yellow flower to be, compared to the blue one, and the greater the probability $p_b$ of the bee landing on the blue flower.
-
in between: the bee’s behavior is a mix between exploiting what the bee deems to be the most nutritious flower and exploring the other one (which is what is expected).
Symetrically:
The “exploitation-exploration trade-off” parameter $β$
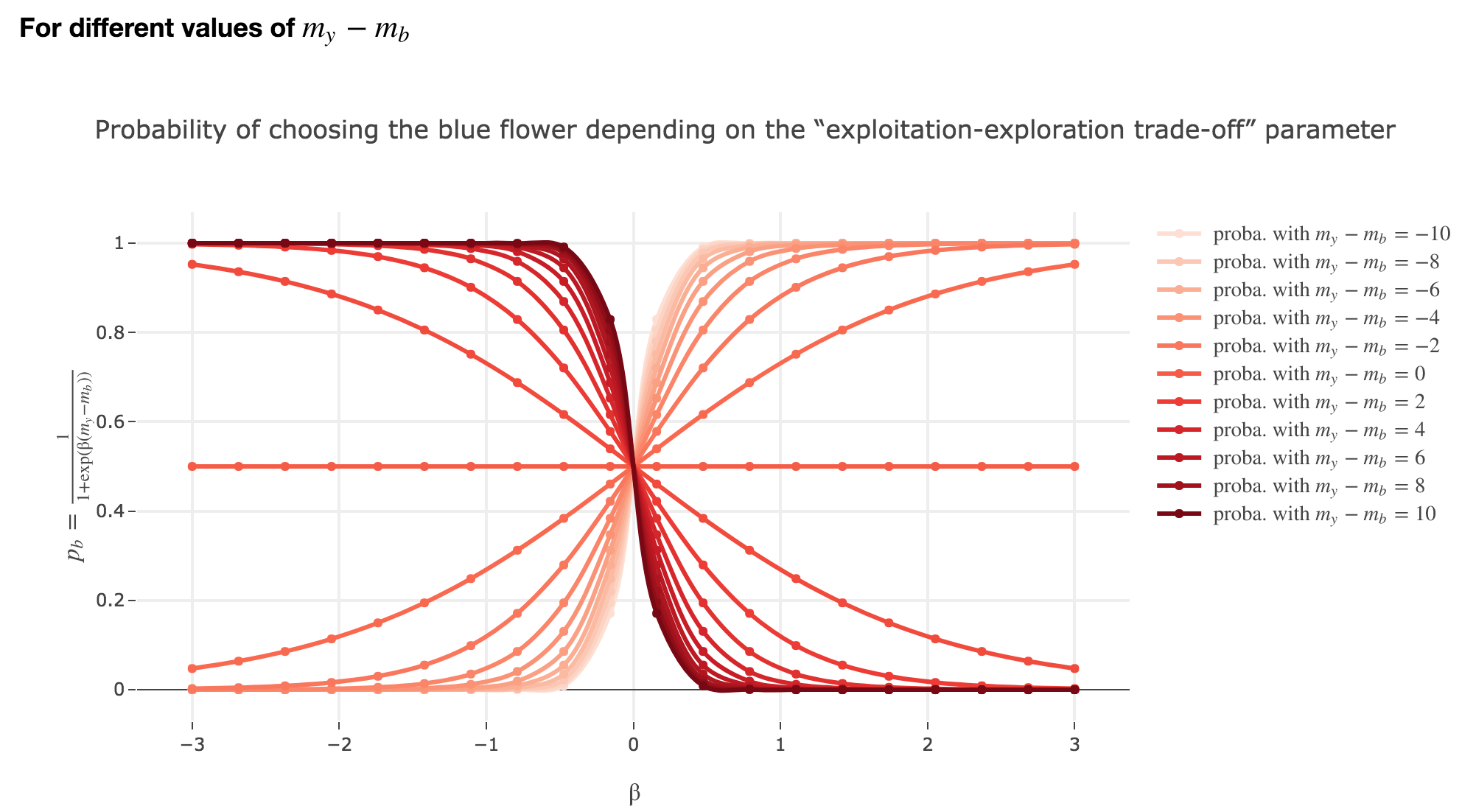
For $β ≥ 0$
As seen in the previous figures: the parameter $β$ plays the same role as the inverse temperature $β ≝ \frac{1}{k_B T}$ in statistical physics. That is, for $β ≥ 0$:
-
When $β ⟶ +∞$: the bigger $β$ is (which corresponds, in physics, to a low temperature/entropy), the more the bee tends to exploit the seemingly most nutritious flower. As a result:
- if $m_y-m_b > 0$ (i.e. the yellow flower seems more avantageous to the bee), the probability of the bee landing on the blue flower rapidly decreases to $0$
- if $m_y-m_b < 0$ (i.e. the blue flower seems more advantageous to the bee), the probability of the bee landing on the blue flower rapidly increases to $1$
-
When $β ⟶ 0$: the lower $β$ is (high temperature/entropy in physics), the more the bee tends to explore the flowers.
Indeed: as $β ⟶ 0$, $p_b$ becomes less and less steep, to such a point that it ends up being the constant function $1/2$ when $β=0$ (at this point, the bee does nothing but exploring, since landing on either of the flowers is equiprobable, no matter how nutritious the bee deems the flowers to be)
For $β < 0$
As
\[p_b(-β, m_y-m_b) = \frac{1}{1 + \exp(-β (m_y-m_b))} = \frac{1}{1 + \exp(β (-(m_y-m_b)))} = p_b(β, -(m_y-m_b))\]The curves for $-β < 0$ are symmetric to those for $β > 0$ with respect to the y-axis, which makes no sense from a behavioral point of vue: it means that the most nutritious a flower appears to the bee, the less likely the bee is to land on it (and conversely)!
2. Dumb bee
Now, let us assume that the bee is “dumb”, i.e. it does not learn from experience: throughout all the trials, the internal reward estimates remain constant: $m_y = 5, \; m_b = 0$.
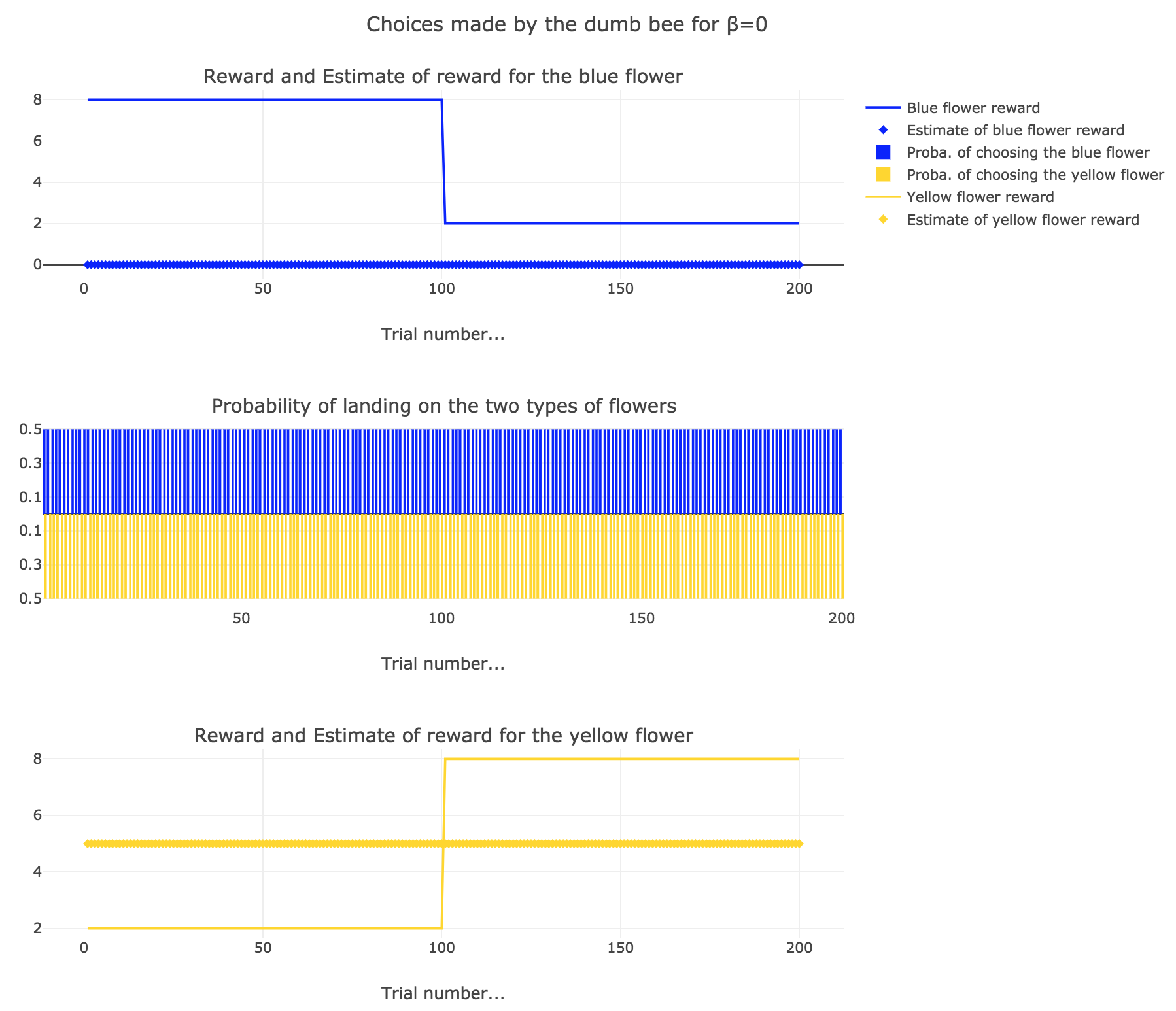
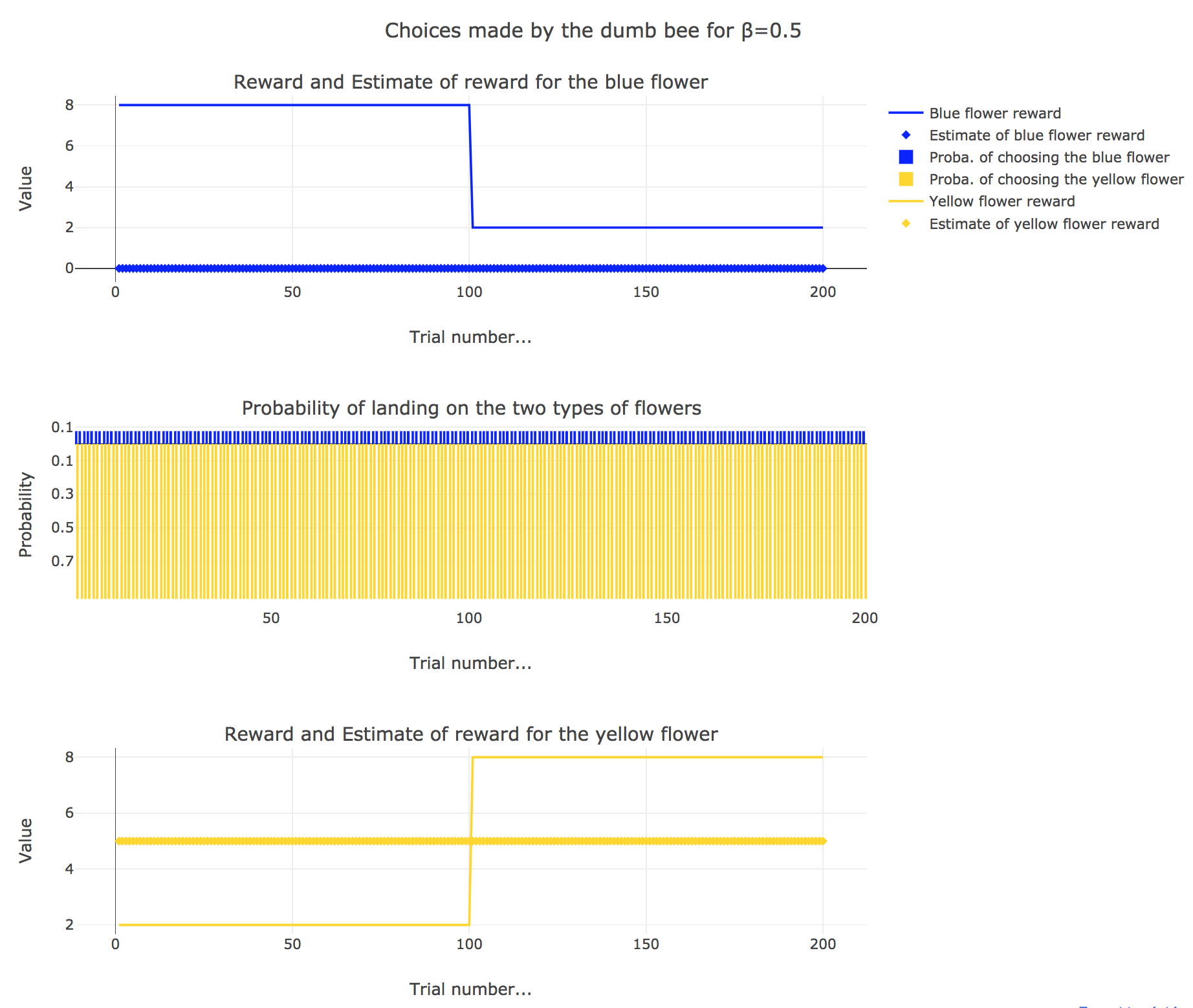
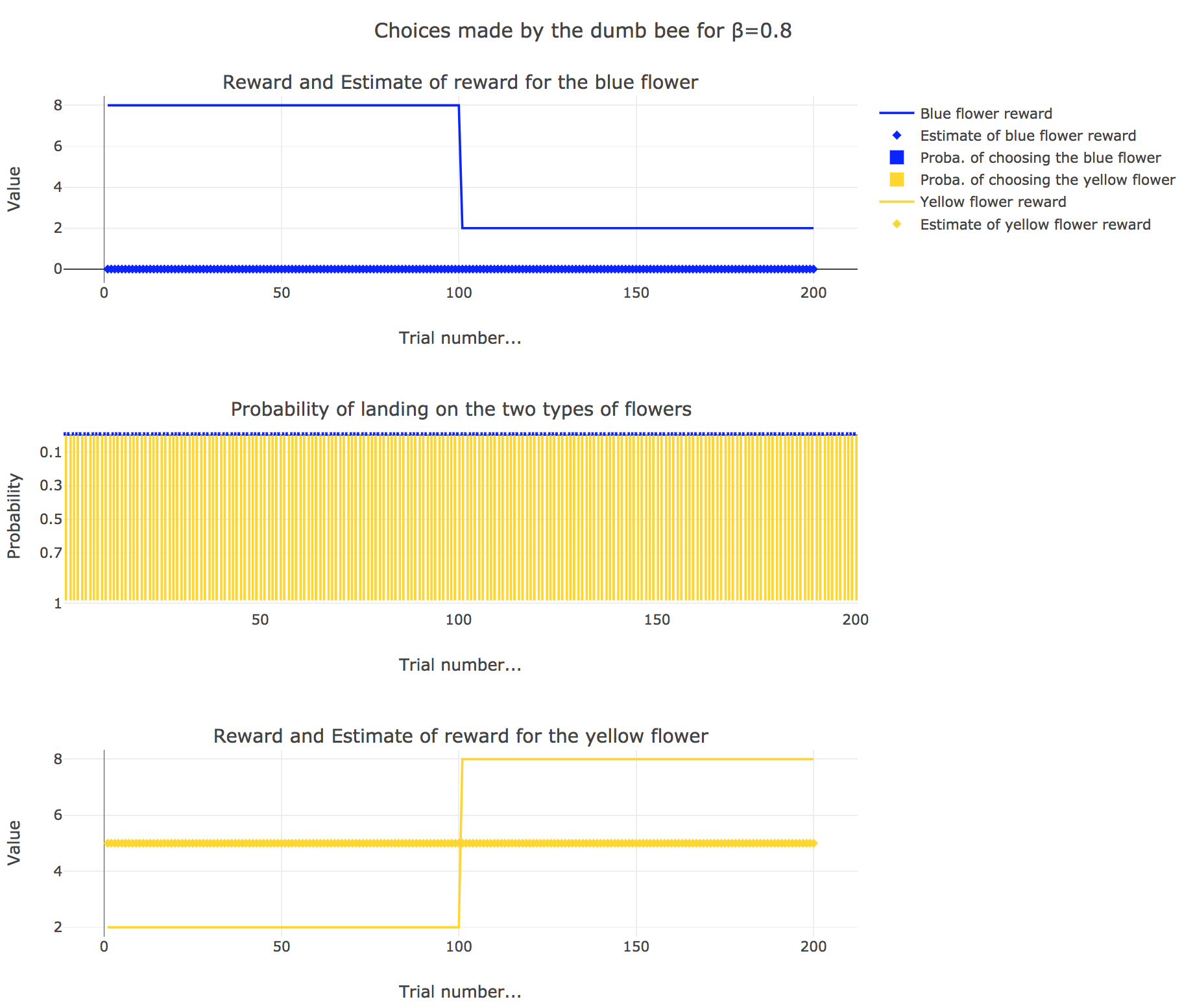
So it appears that
-
for $β = 0$: the bee’s behavior is the most exploratory one: the probability of landing on a blue flower as well as a yellow flower is $1/2$, irrespective of the internal estimates $m_b$ and $m_y$
-
for $β = 0.5$: this $β$ corresponds to a perfectly balanced exploration-exploitation tradoff, but here: as $m_y = 5$ is significantly higher that $m_b = 0$, $p_y ≝ 1-p_b » p_b$ (which are constant, as the internal estimates are constant)
-
for $β = 1$: the bee’s behavior is the most exploitative one. As $m_y > m_b$, $p_y ≃ 1$: the bee keep exploiting the flower it deems the most nutritious (i.e. the yellow ones).
On the whole, this behavior can reasonably be called “dumb”, since the bee takes no account of the actual rewards of the flowers whatsoever (its internal estimates remain constant and don’t depend on these actual rewards).
3. Smart bee
Now let us suppose that the bee is “smart”, i.e. it can learn from its experiences. Whenever it visits a flower, it updates its estimated reward as follows:
\[\begin{align*} m_b &→ m_b + ε(r_b − m_b)\\ m_y &→m_y +ε(r_y − m_y) \end{align*}\]Given a learning parameter $ε = 0.2$ and the initial assumptions about flower reward from above ($m_y = 5, m_b = 0$), simulate the bees sequence of choices during the two days. How do the reward estimates change over time? Explore the case of purely explorative behavior ($β = 0$) and the case of strongly exploitative behavior ($β = 1$). What do you observe?
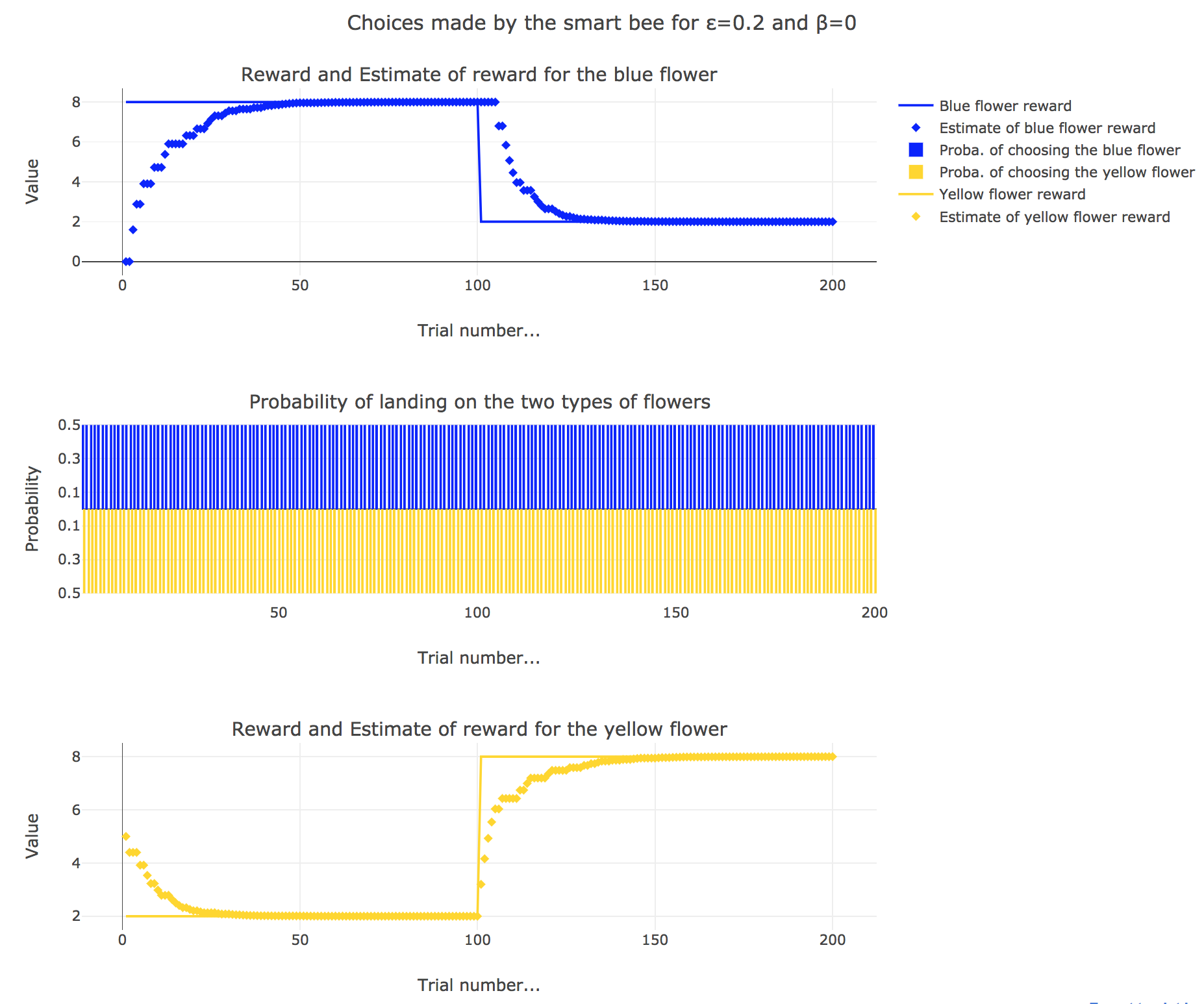
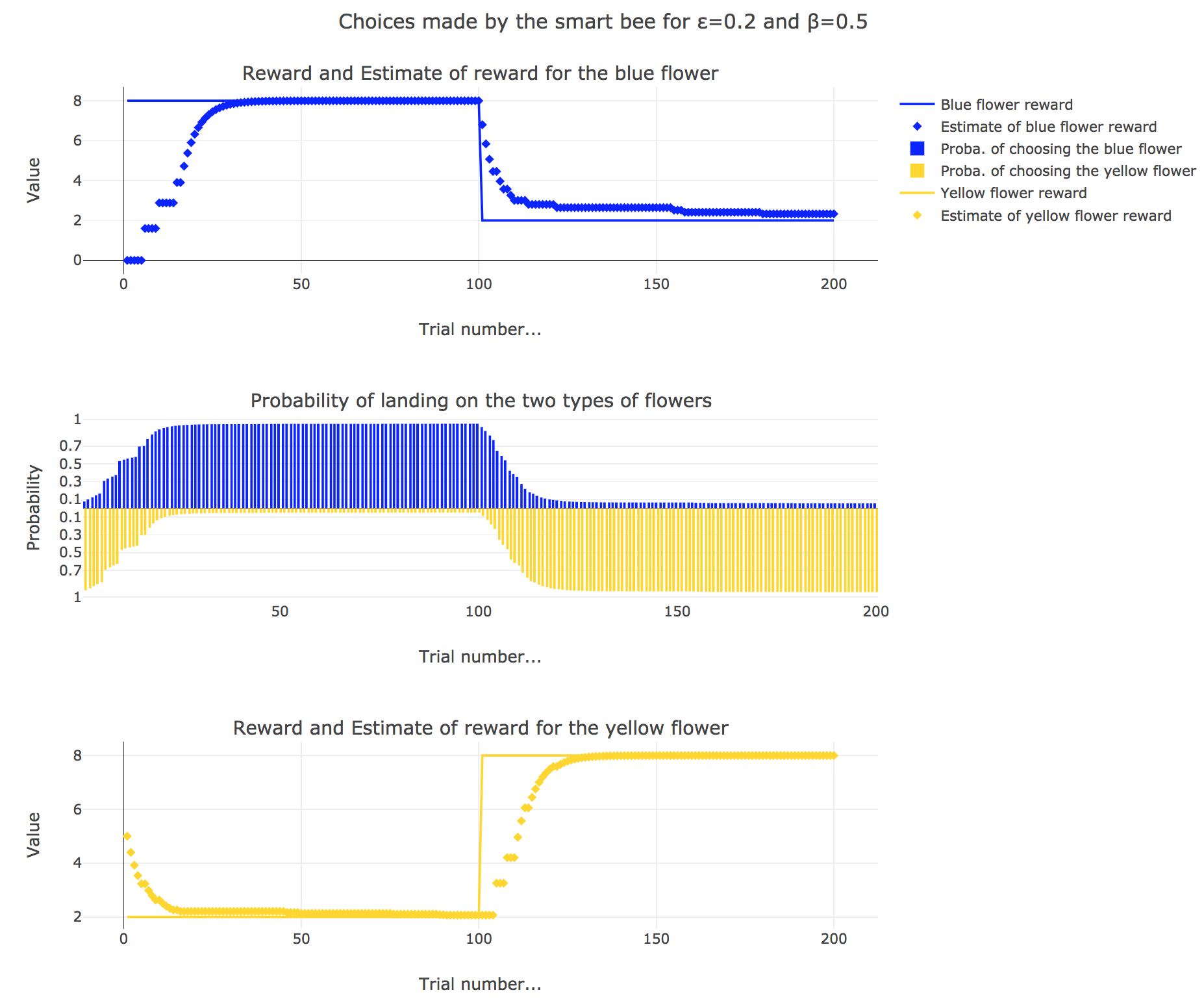
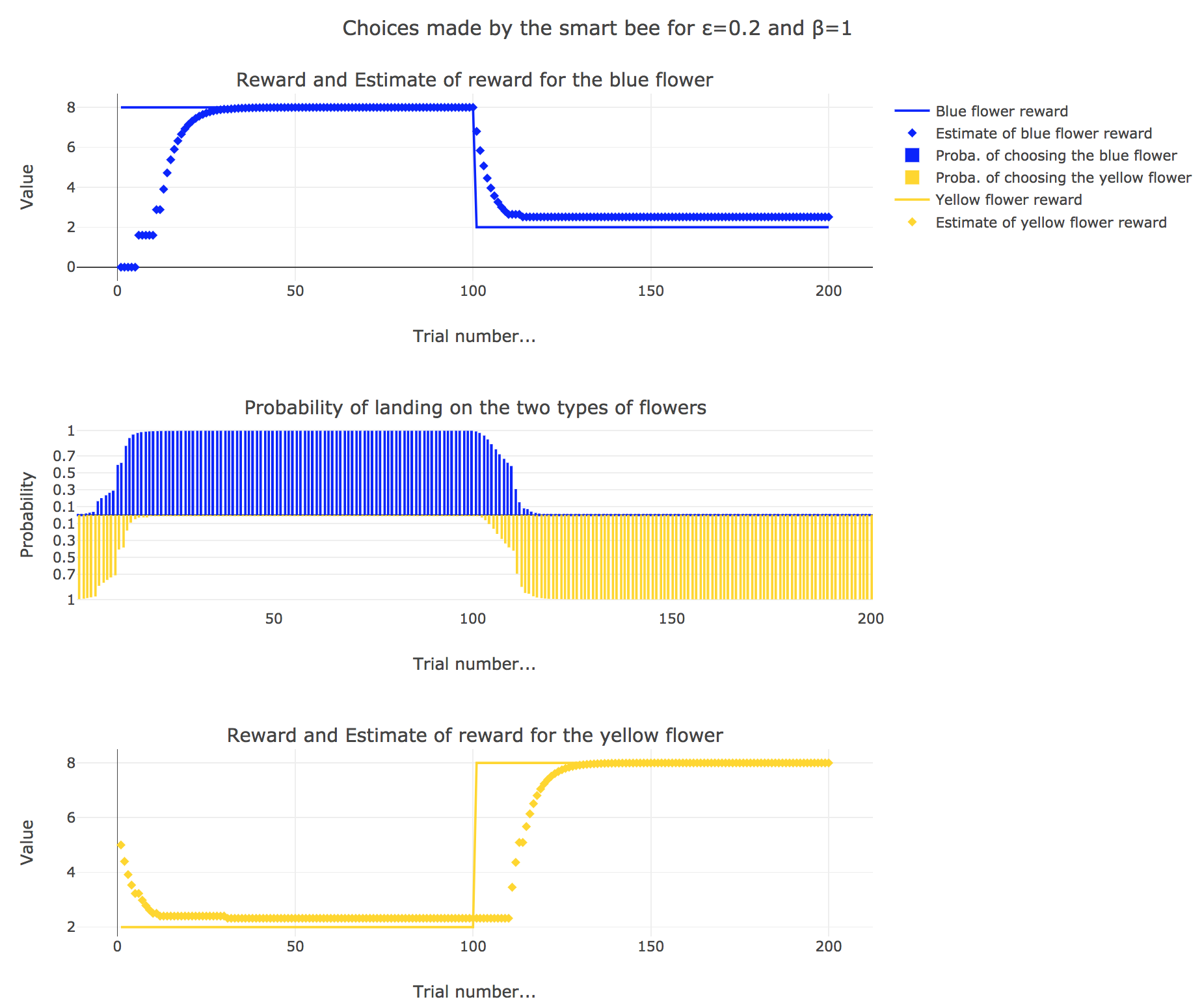
It appears that
-
for $β = 0$: no surprise, the bee’s behavior is the most exploratory one: the probability of landing on a blue flower as well as a yellow flower is $1/2$, irrespective of the internal estimates $m_b$ and $m_y$
-
for $β = 1$: the bee’s behavior is the most exploitative one. Similarly to the Rescola-Wagner rule, the updating rule makes the internal estimates converge toward the actual rewards of the flowers, and as result: the exploitative behavior causes the probability $p_b$ (resp. $p_y ≝ 1-p_b$) to match the evolution of the internal estimate $m_b$ (resp. $m_y$) when $m_b > m_y$ (resp. $m_y > m_b$): the bee exploit the flower type which has the highest current estimate.
-
for $β = 0.5$: it is a mixed behavior bewteen exploitation and exploration: compared to the case $β=1$, there are some discrepancies in the update of the internal estimates, since the bee may not always exploit the flower type which has the best current estimate (exploratory behavior).
On the whole, this behavior can reasonably be called “smart”, since the bee, depending on the value of $β$:
takes more or less into account the actual rewards of the flowers by exploiting the seemingly most nutritious flower (exploitation, increasing with $β$)
while, from time to time, completely ignoring its internal estimates and exploring the other flower (exploration, decreasing with $β$)
Leave a comment