Fiche-Résumé : Cours 1 à 5

Version PDF

Chapitre 1 : Cardinalité

I. Ensembles finis

Généralités

1. Si il existe une surjection de $⟦1,n⟧$ sur $E$, alors $E$ est fini de card $\leq n$
2. Si il existe une injection de $⟦1,n⟧$ sur $E$, alors $E$ est de card $≥ n$

Si $\vert E\vert = n, \vert F \vert =m$ :

• $\vert E \times F \vert = nm$

• $\vert E ∪ F\vert = \vert E\vert + \vert F\vert - \vert E ∩ F\vert$
• $\vert 𝒫(E) \vert = 2^n$,

Coefficients binomiaux

Identités :

• \[2^n = \sum\limits_{k=0}^n \binom{n}{k}\]

  Idée clé : $𝒫(E) = \bigsqcup\limits_{k=0}^n \lbrace\text{parties de card } k\rbrace$

• \[\binom{n}{k} = \binom{n}{n-k}\]

  Idée clé : passage au complémentaire.

• Le triangle de Pascal : si $n ∈ ℕ^*$ : \(\binom{n-1}{k} + \binom{n-1}{k-1} = \binom{n}{k}\)

  Idée clé: deux types de parties de cardinal $k$ : celles qui contiennent $n$ et celles qui ne le contiennent pas.

• \[\binom{n}{k} = \sum\limits_{j=k}^n \binom{j-1}{k-1}\]

  Idée clé : parties de card $k$ selon leur plus grand élément $∈ ⟦k, n⟧$

• Identité de Vandermonde :

\[\binom{m+n}{k} = \sum\limits_{0\leq i \leq m, k-n \leq i \leq k} \binom{m}{i}\binom{n}{k-i}\]

Idée clé : parties de card $k$ de $E∪F = ⟦1,m+n⟧$ selon les cardinaux des traces sur $E$ / sur $F$.

• \[k \binom{n}{k} = n \binom{n-1}{k-1}\]

  Idée clé: double comptage de $\lbrace (i,𝕱) \, \vert \, 𝕱 ⊆ F, \vert 𝕱\vert =k, 1\leq i \leq k \rbrace$

  Corollaire :

  \[\binom{n}{k} = \frac{n!}{k!(n-k)!}\]

Principe des tiroirs

Principe des tiroirs : Si $f : E ⟶ F$ et $\vert E\vert > \vert F\vert $, au moins deux éléments ont la même image.

Applications :

Pumping Lemma :

Soit $L$ un langage rationnel :

$∃ N ∈ ℕ; ∀ 𝜔 ∈ L,$

\[\vert w\vert \geq N ⟹ ∃ x,y,z; \begin{cases} 𝜔 ≝ xyz ∈ L \\ \vert y\vert \leq N \end{cases} ∧ ∀n∈ℕ, xy^nz ∈ L\]

Lemme d’Erdös

Lemme d’Erdös :

Soit $(x_i)_{i ∈ ⟦1, n^2+1⟧}$ une famille d’entiers naturels.

Alors il y a au moins une sous-famille croissante de card $n+1$ ou un sous-famille décroissante de card $n+1$.

Idée clé : card d’une plus grande sous-famille croissante/décroissante qui débute/termine en $x_i$, puis contradiction avec le principe des tiroirs.

Formule du crible / de Poincaré / Principe d’inclusion-exclusion

$E_1, …, E_n ⊆ X$

\[\left\vert \bigcup_{1}^n E_i \right\vert = \sum\limits_{\substack{k ∈ ⟦1,n⟧ \\ 1 \leq i_1 < ⋯ < i_k \leq n}} (-1)^{k-1} \bigcap_j E_{i_j}\]

Idée clé : calcul de \(1_X - 1_{\bigcup E_i} = \prod\limits_{1}^n (1_X - 1_{E_i})\)

II. Ensembles Dénombrables

Ensemble dénombrable :

• au sens strict : en bijection avec $ℕ$
• au sens large : en bijection avec $ℕ$ OU fini

Proposition : Tout ss-ensemble infini de $ℕ$ est dénombrable.

Idée clé : \(f ≝ \begin{cases} ℕ ⟶ E \\ 0 \mapsto \min(E) \\ n > 0 \mapsto \min(E\backslash\{f(0), ⋯, f(n-1)\}) \end{cases}\)

Corollaire : Tout ensemble $E$ tel qu’∃ une injection de $E$ dans $ℕ$ est dénombrable au sens large.

Bijections classiques :

\[\begin{cases} ℤ ⟶ ℕ \\ n \mapsto \begin{cases} 2n \text{ si } n\geq 0 \\ -2n-1 \text{ sinon.} \\ \end{cases}\end{cases}\] \[\begin{cases} ℕ^n ⟶ ℕ \\ (a_1, ⋯, a_n) \mapsto 2^{a_1} 3^{a_2} ⋯ \underbrace{p_n^{a_n}}_{p_n : n\text{-ième nombre premier}} \end{cases}\] \[\begin{cases} ℚ ⟶ ℕ \\ x = \underbrace{𝜀\dfrac p q}_{𝜀=±1, \, \, p∧q=1} \mapsto \begin{cases} 2^p 3^q \text{ si } 𝜀=1 \\ 2^p 5^q \text{ si } 𝜀=-1 \text{ et } p\neq 0 \\ \end{cases}\end{cases}\]

Proposition: Une réunion d’ensembles dénombrables est dénombrable.

Idée clé : \(\begin{cases} \bigcup E_i ⟶ ℕ\times ℕ \\ x \mapsto (i, f_i(x)) \end{cases}\) où $i = \min{j \vert x∈E_j}$

Ensembles non dénombrables :

• $ℝ$ : Idée clé : argument diagonal de Cantor.

III. Equipotence

Ensembles équipotents :

ensembles en bijection.

Théorème de Cantor : $E$ et $𝒫(E)$ ne sont pas équipotents.

Idée clé : par l’absurde, avec $X ≝ \lbrace x ∈ E \vert x \not\in f(x)\rbrace$

Chapitre 2 : Relations

I. Relations binaires

Relation binaire sur une ensemble $E$ :

une partie $R⊆E\times E$

Notation: $xRy ⟺ (x,y)∈R$

Clôture transitive $R^{**}$ de $R$ :

\[∀x, y ∈E, xR^{**}y ⟺ ∃n\geq 1, x_1, ⋯, x_n ∈ E ; \\ (x_0 = x) ∧ (x_i R x_{i+1} ∀i∈⟦0,n-1⟧) ∧ (x_n = y)\]

Relation d’équivalence $R$ :

relation binaire réflexive, symétrique et transitive.

• $x ∈ 𝒞(x)$
• $∀ x, y ∈ E, xRy ⟺ 𝒞(x) = 𝒞(y)$
• $∀ x, y ∈ E, xRy ⟺ 𝒞(x) ∩ 𝒞(y) \neq ∅$

Corollaire :

• L’ensemble des classes d’équivalence de la relation d’éq $R$ sur $E$ définit une partition de $E$.
• Réciproquement : toute partition de $E$ définit une relation d’éq dont les classes d’éq sont les éléments de la partition.

Ensemble quotient $E/R$ :

ensemble des classes d’éq de $R$ sur $E$.

Surjection canonique :

L’application \(𝜋 : \begin{cases} E ⟶ E/R \\ x \mapsto 𝒞(x) ≝ \{y ∈ E; xRy\} \end{cases}\)

Proposition : Soit $f : E ⟶ F$ compatible avec $R$, i.e

\[∀x, y ∈ E, xRy ⟹ f(x)=f(y)\]

Alors il existe $\bar{f} : E/R ⟶ F$ tq le diagramme suivant est commutatif : \({\displaystyle {\begin{matrix}E&\displaystyle {\xrightarrow {f}}&F\\\pi \downarrow &\displaystyle \nearrow \bar{f}\\E/R\end{matrix}}}\)

Relation d’ordre $≤$ :

Relation binaire réflexive, antisymétrique, transitive.

Exs :

• $(ℕ, ≤), (ℝ, ≤)$ (ordres totaux)

• ordre lexicographique

• Dans $ℕ^k$ : $(m_1, ⋯, m_k) ≤ (n_1, ⋯, n_k)$ si c’est le cas pour toutes les composantes (ordre partiel).

• L’inclusion dans $𝒫(E)$ (ordre partiel).
• La divisibilité dans $ℕ^*$ (ordre partiel).

Chaîne :

Ensemble totalement ordonné.

Antichaîne :

Ensemble où deux éléments distincts ne sont pas comparables.

Successeur :

Soient $x, y ∈ E$ (muni de $≤$). $y$ est le successeur de $x$ ssi : \((y > x) ∧ ∀z∈E, y≥z≥x ⟹ y=z\) ($y$ est plus grand que $x$, et il n’y a rien entre les deux).

Proposition : Si $E$ est fini, $≤$ est la clôture transitive de la relation “successeur”.

Plus petit élément = minimum $\bot$ / Plus grand élément = maximum $\top$ :

\[∀x∈E, \bot \leq x \, \, / \, \, ∀x∈E, \top \geq x\]

Élément maximal / minimal $x$ dans $F$ :

\[∀y∈F, y ≥ x ⟹ y=x \, \, / \, \, ∀y∈F, y ≤ x ⟹ y=x\]

• Plus petit/grand élément ⟹ Élément minimal/maximal

MAIS

• Unique élément minimal/maximal $\not⟹$ Plus petit/grand élément

À part pour les ensembles finis :

Si $F$ fini admet un unique élément maximal, alors c’est un maximum.

Majorant / Minorant $y∈E \supset F$ de $F$ :

\[∀x∈F, y ≥ x \, \, / \, \, ∀x∈F, y ≤ x\]

Borne supérieure / inférieure :

Minimum / maximum de l’ensemble des majorants / minorants, s’il existe.

• Plus grand / petit élément ⟹ Borne sup / inf

• Borne supérieure appartenant à l’ensemble ⟹ maximum

Exs :

1) $(ℕ\backslash{0}, \vert )$, $F={a_1, ⋯, a_n}$ :

• les majorants : multiples communs aux $a_i$
  • borne sup : $ppcm(a_1, ⋯, a_n)$.
• les minorants : diviseurs communs aux $a_i$
  • borne inf : $pgcd(a_1, ⋯, a_n)$.

2) $(E, ≤) = (𝒫(X), ⊆)$, $F = {Y_1, ⋯, Y_n}$ :

• Borne sup : $\bigcup_i Y_i$
• Borne inf : $\bigcap_i Y_i$

Treillis

Treillis :

Ensemble ordonné dans lequel toute paire (d’éléments) admet une borne sup et une borne inf.

Treillis complet :

Si, de plus, pour toute partie $F ⊆ E$, $F$ admet un borne sup et une borne inf.

NB : Un treillis complet a un plus grand / petit élément.

Exs:

1) $(ℕ\backslash{0}, \vert )$ : treillis non complet

2) $(𝒫(X), ⊆)$ : treillis complet :

• Borne sup de $S⊆𝒫(X)$ = $\bigcup_{Y∈S} Y$
• Borne inf de $S⊆𝒫(X)$ = $\bigcap_{Y∈S} Y$

Th de Knaster-Tarski : Soit $(E,≤)$ un treillis complet, $f: E ⟶ E$ monotone.

Alors $f$ admet un plus petit / plus grand pt fixe.

Idée clé : c’est la borne inf / sup de $\lbrace x∈E; x\geq f(x)\rbrace$ / $\lbrace x∈E; x\leq f(x)\rbrace$

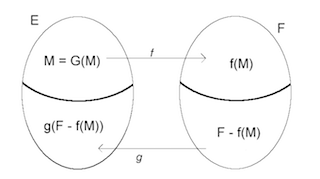
Théorème de Cantor-Bernstein : Si il existe une injection de $E$ dans $F$ et une injection de $F$ dans $E$, alors $E$ et $F$ sont équipotents.

Idée clé : Application de Knaster-Tarski

Théorème de Bourbaki-Witt :

Soit $(X, ≤)$ un ensemble ordonné tel que toute chaîne non vide admet une borne supérieure.

Soit $f : X ⟶ X$ une application telle que $∀x ∈ X, x ≤ f(x)$.

Alors $f$ admet un point fixe.

Lemme de Zorn : Soit $X$ un ensemble ordonné dans lequel toute chaîne admet une borne supérieure. Alors $X$ admet un élément maximal.

Idée clé : Appliquer Bourbaki-Witt à $\lbrace\text{chaînes de } X\rbrace$ en supposant par l’absurde qu’aucune chaîne n’est maximale.

Chapitre 3 : Structures algébriques

0. Catégories

Catégorie :

Il y a des :

• objets : $E, F, G…$
• flèches : $Hom(E,F)$ : on y manipule des applications $E⟶F$ qui sont compatibles avec la structure.

$F : 𝒞⟶𝒞’$ foncteur.

Si $E$ est un objet, $F(E)$ objet.

Si $f ∈ Hom_𝒞(E,G)$, $F(f)∈ Hom_𝒞(F(E),F(G))$

Problème universel : objet libre

$L(X)$ est libre sur $X$ si pour tout $E$ dans $𝒞$, pour tout $f: X ⟶E$, il existe un unique $\widehat{f}$ dans $Hom_𝒞(L(X),E)$ qui prolonge $f$.

I. Semi-groupes et monoïdes

Partie génératrice du monoïde $M$ :

$X⊆M$, telle que $⟨X⟩=M$. ($X$ engendre $M$)

Congruence :

Une relation d’éq $\sim$ telle que \(m_1 \sim m_2 ⟹ ∀u,v ∈ M, um_1 v \sim u m_2 v\)

Prop : Une congruence $\sim$ sur $M$ est compatible avec la loi de monoïde, i.e : \(m_1 \sim m_2 ∧ n_1 \sim n_2 ⟹ m_1 n_1 \sim m_2 n_2\)

Propriété universelle : Soit $f: M⟶ N$ un morphisme de monoïdes, $\sim$ une congruence sur $M$ compatible avec $f$, i.e tq $m_1 \sim m_2 ⟹ f(m_1) = f(m_2)$

Alors : il existe un morphisme de monoïdes $f$ de $M/\sim$ dans $N$ tq \(f = \widehat{f} \circ 𝜋\)

Cas particulier : si : \(m_1 \sim m_2 ⟺ f(m_1) = f(m_2)\)

$\widehat{f}$ est injectif.

2. Monoïdes libres

Prop : Pour un monoïde $M$, et une application $f : 𝛴 ⟶ M$, il existe un unique morphisme de monoïdes $\widehat{f}$ de $𝛴^$ dans $M$ tq \(f = \widehat{f}\circ i\) ($i$ : injection de $𝛴$ dans $𝛴^$)

Application “longueur” :

C’est l’unique prolongement de \(\begin{cases} 𝛴 ⟶ ℕ \\ a \mapsto 1 \end{cases}\) en un morphisme de $𝛴^*$ dans $ℕ$ (on le note $\vert \cdot\vert $).

Base $X ⊆ M$ :

tout élément de $M$ se décompose de façon unique comme un produit d’éléments de $X$.

Monoïde libre :

Monoïde isomorphe à un ss-monoïde de $𝛴^*$ qui admet une base.

Code :

une partie $X⊆M$ tq \(∀u_i, v_i ∈X, u_1 ⋯ u_n = v_1 ⋯ v_p ⟹ (n=p) ∧ (∀i, u_i = v_i)\)

NB : Soit $L$ un ss-monoïde de $𝛴^*$ :

• si on note $X$ les mots qui se décomposent de façon non triviale dans $L$ : alors $L = ⟨X⟩$

• $L$ est libre ssi \(∀w∈𝛴^*, ∃ u,v ∈ L; uw ∈ L ∧ wv ∈ L\) alors $w∈L$

Corollaire : Ss-mon. libres de $𝛴^*$ : stables par intersection

Corollaire : Si $X⊆𝛴^*$, existence d’un plus petit ss-mon. libre contenant $X$ : enveloppe libre de $X$.

Th de défaut : Si $X⊆𝛴^*$ et on suppose $X$ fini. Soit $L$ l’enveloppe libre de $X$, $Y$ le code de $L$.

Alors si $X$ n’est pas code, $\vert Y\vert <\vert X\vert$

3. Monoïdes finis

Si $M=⟨x⟩$, si $m+p$ est le plus petit possible tel que $x^{m+p} = x^m$, la structure de $M$ est donnée par :

\[M= \{𝜀, x, ⋯, x^{m}=x^{m+p}, ⋯, x^{m+p-1}\}\]

Groupes

Sous-groupe distingué/normal $H ⊆ G$ :

Une des conditions équivalentes suivantes est vraie :

• $∀g ∈ G, gH = Hg$
• $∀g ∈ G, gHg^{-1} = H$
• stable par automorphismes intérieurs

Une relation d’équivalence “compatible” est de la forme : “∃ $H$ ss-groupe distingué” $ssi$ :

\[g_1 \sim g_2 ⟺ g_1 H = g_2 H\]

Alors $H = \overline{1}$ est un sous-groupe distingué.

Comme $G$ est un groupe, et $𝜋 :G ⟶ G/\sim = G/H, g \mapsto gH$ surjective, $G/H$ est un groupe, d’élément neutre $𝜋(1)=H$.

Prop : Soit $𝜑 : G_1 ⟶ G_2$ un morphisme de monoïdes.

$Ker(𝜑)$ est un ss-groupe distingué.

$𝜑$ se factorise :

\[{\displaystyle {\begin{matrix}G_1&{\xrightarrow {𝜑}}&G_2\\𝜋 \downarrow &\nearrow \widehat{g}\\G/\sim \end{matrix}}}\]

Groupes libres :

• Groupe libre à un générateur $≃ ℤ$
• $ℤ/nℤ = ⟨x \vert x^n=1⟩$
• Groupe diédral $D_{2n} ≃ ⟨𝜌, 𝜎 \vert 𝜌^n=1, 𝜎^2=1, 𝜎𝜌𝜎^{-1}=𝜌^{-1}⟩$ :
  • rotation d’angle $\pm 2𝜋/3$
  • 3 symétries

Groupes abéliens libres de type fini :

Groupes isomorphes à $ℤ^n$

Groupes finis

Thm de Lagrange : si $H$ est un sg de $G$, $\vert H \vert / \vert G \vert$

3. Groupe opérant sur un ensemble.

Opération de de $G$ sur l’ensemble $E$ :

c’est la donnée d’une application

\[\begin{cases} G\times E ⟶ E \\ (g,x) \mapsto g\cdot x \end{cases}\]

telle que :

• $∀x∈E, 1\cdot x = x$ ($1$ opère comme $id$ sur $E$)
• $∀g, g’∈E, ∀x∈G, g\cdot (g’ \cdot x) = (gg’)\cdot x$

Alors :

\[𝜑 ≝ \begin{cases} G ⟶ 𝕾(E) \\ g \mapsto g\cdot \bullet \end{cases}\]

est un morphisme de groupes.

Réciproquement : tout morphisme $𝜑$ de $G$ dans $𝕾(E)$ définit une opération de $G$ sur $E$.

Orbites :

classes d’équivalence pour la relation \(∀x, y ∈E, x\sim y ⟺ ∃g∈G; x=g\cdot y\)

Stabilisateur de $x$ :

le sous-groupe : \(H_x ≝ \{g ∈ G \vert g\cdot x = x\}\)

\[\begin{cases} G ⟶ 𝜔_x \\ g \mapsto g\cdot x \end{cases}\]

est une application surjective telle que :

\[∀g, g'∈G, g\cdot x = g'\cdot x ⟺ ∃h∈H_x; g = g'h\]

d’où :

\[|G| = |H_x||𝜔_x|\]

Fixateur $Fix(g)$ de $g∈G$ agissant sur $E$ :

ensemble des points fixes de $g$ dans $E$.

Formule (qui n’est pas) de Burnside : Soit $G$ un groupe fini opérant sur un ensemble fini $E$.

Soit $k = \vert E/G\vert$ le nombre d’orbites de $E$ sous l’opération de $G$.

\[k = \vert E/G\vert = \frac{1}{|G|}\sum\limits_{g∈G}|Fix(g)|\]

Idée clé : Double comptage de $\lbrace (g,x) \vert g∈G ∧ x∈E ∧ g\cdot x =x \rbrace$

Anneaux

Idéal $I$ d’un anneau $A$ :

sous-groupe additif tel que : \(∀a∈A, ∀x∈I, ax∈I\)

NB : $A/I$ est muni d’une structure d’anneau.

Séries formelles

\[𝕂[[X]] ≝ \{\sum\limits_{n≥0} a_n X^n, (a_n) ∈ 𝕂^ℕ\}\]

• addition usuelle, produit de Cauchy

Valuation $v : 𝕂[[X]]⟶ℕ∪\lbrace ±∞\rbrace$ d’une série formelle :

\[v(\sum\limits_{n≥0} a_n X^n) = \begin{cases} +∞ \text{ si } ∀n, a_n = 0 \\ \min(i, a_i≠ 0) \text{ sinon} \end{cases}\]

$d$ distance ultramétrique :

\[d(\sum\limits_{n≥0} a_n X^n, \sum\limits_{n≥0} b_n X^n) = \exp(-v(\sum\limits_{n≥0} a_n X^n - \sum\limits_{n≥0} b_n X^n))\]