Analyse : Fonction de McCarthy
Oraux
On note \(g\) le prolongement \(2\)-périodique à \(\mathbb{R}\) de la restriction à \([-1,1]\) de \(\vert\bullet\vert\). On pose \(f {\overset{\small{\text{déf}}}{=}}\left\{ \begin{array}{l l} \mathbb{R} &\to \mathbb{R} \\ x &\mapsto \sum\limits_{k \geq 0} \left(\frac{3}{4}\right)^k g(4^k x) \end{array} \right.\) Montrer que \(f\) continue mais non dérivable en aucun point.
-
Continuité : la série de fonction \(f\) converge normalement, puisque \(\vert g\vert\) est majorée par \(1\).
-
Non-dérivabilité : Soit \(x \in \mathbb{R}\). Montrons que le taux d’accroissement \(\tau_x {\overset{\small{\text{déf}}}{=}}\frac{f(x+\bullet) - f(x)}{\bullet}\) diverge en \(0\). Il suffit d’exhiber une suite \((h_n)_{n \in \mathbb{N}}\) telle que \(\lim_{n \to \infty} \left\vert \frac{f(x+h_n) - f(x)}{h_n} \right\vert = \infty\)
On pose : \(h_n {\overset{\small{\text{déf}}}{=}}\begin{cases} \, \hspace{1em}\dfrac{1}{2\cdot 4^n} & \mbox{si } 4^n x - \lfloor 4^n x \rfloor < 1/2, \\ \, \, -\dfrac{1}{2\cdot 4^n} & \mbox{sinon.} \end{cases}\) Alors :
-
\(\left\vert \dfrac{g(4^n (x+h_n)) - g(4^n x)}{4^n h_n}\right\vert = 1\) : En effet, aucun entier ne se trouve dans l’intervalle ouvert d’extrémités \(4^n x\) et \(4^n (x + h_n)\) :
-
Si \(4^n x - \lfloor 4^n x \rfloor < 1/2\) : \(4^n x < \lfloor 4^n x \rfloor + 1/2 \Longrightarrow 4^n (x + h_n) = 4^n x + 1/2 < \lfloor 4^n x \rfloor + 1\), donc \(\big]4^n x , 4^n (x + h_n) \big[ \, \varsubsetneq \, \big[\lfloor 4^n x \rfloor, \lfloor 4^n x \rfloor + 1\big]\)
-
Si \(4^n x - \lfloor 4^n x \rfloor \geq 1/2\) : \(4^n x \geq \lfloor 4^n x \rfloor + 1/2 \Longrightarrow 4^n (x + h_n) = 4^n x - 1/2 \geq \lfloor 4^n x \rfloor\), donc \(\big] 4^n (x + h_n) , 4^n x \big[ \, \varsubsetneq \, \big[\lfloor 4^n x \rfloor, \lfloor 4^n x \rfloor + 1\big]\) Donc la pente \(\, \dfrac{g(4^n (x+h_n)) - g(4^n x)}{4^n h_n}\) vaut \(1\) en valeur absolue, par définition de \(g\).
-
-
Pour tout \(k \geq n+1\), \(\, \, g(4^k x) = g(4^k(x+h_n))\) : En effet : \(\vert 4^k h_n\vert = \dfrac{4^{k-n}}{2} \in 2\mathbb{N}\), d’où \(4^k h_n\) est un entier pair, et le résultat découle de la \(2\)-périodicité de \(g\).
-
Pour tout \(k \in ⟦ 0, n ⟧\), \(\, \, \exists \varepsilon_{n,k} \in \{-1, 1\}; \, \dfrac{g(4^k (x+h_n)) - g(4^k x)}{h_n} = 4^k \varepsilon_{n,k}\): En effet : l’intervalle ouvert d’extrémités \(4^k x\) et \(4^k (x + h_n)\) ne contient pas d’entier, sinon ce serait aussi le cas de l’intervalle d’extrémités \(4^{n-k} 4^k x\) et \(4^{n-k} 4^k (x + h_n)\), ce que (a) exclut. Donc la pente \(\, \dfrac{g(4^k (x+h_n)) - g(4^k x)}{4^k h_n}\) vaut \(1\) en valeur absolue, par définition de \(g\).
-
\(\tau_x(h_n) = \left\vert \frac{f(x+h_n) - f(x)}{h_n} \right\vert\) diverge en \(+\infty\) : \(\begin{aligned} \left\vert \dfrac{f(x+h_n) - f(x)}{h_n} \right\vert \, &= \, \left\vert \displaystyle\sum\limits_{k \geq 0} \left(\frac{3}{4}\right)^k \frac{g(4^k (x+h_n)) - g(4^k x)}{h_n} \right\vert \\ &= \, \left\vert \displaystyle\sum\limits_{k = 0}^n \left(\frac{3}{4}\right)^k \frac{g(4^k (x+h_n)) - g(4^k x)}{h_n} \right\vert && \text{\big(par (b) \big)} \\ &\geq \, \left(\frac{3}{4}\right)^n \left\vert \frac{g(4^n (x+h_n)) - g(4^n x)}{h_n} \right\vert - \left\vert \displaystyle\sum\limits_{k = 0}^{n-1} \left(\frac{3}{4}\right)^k \frac{g(4^k (x+h_n)) - g(4^k x)}{h_n} \right\vert && \text{({\sc IT} n°2)} \\ &\geq \,\left(\frac{3}{4}\right)^n \left\vert 4^n \right\vert - \displaystyle\sum\limits_{k = 0}^{n-1} \left(\frac{3}{4}\right)^k \left\vert \frac{g(4^k (x+h_n)) - g(4^k x)}{h_n} \right\vert && \text{(par (a))} \\ &\geq \, 3^n - \displaystyle\sum\limits_{k = 0}^{n-1} \left(\frac{3}{4}\right)^k\cdot 4^k && \circledast \end{aligned}\) En effet : pour tout \(k \in ⟦ 0, n-1 ⟧\), les pentes \(\dfrac{g(4^k (x+h_n)) - g(4^k x)}{4^k h_n}\) sont inférieures (et même égales, par (c)) à \(1\) en valeur absolue, par définition de \(g\). Donc \(\begin{aligned} \left\vert \dfrac{f(x+h_n) - f(x)}{h_n} \right\vert \, &\geq \, 3^n - \frac{3^n - 1}{2} \\ &= \, \frac{3^n + 1}{2} \underset{n \to \infty}{\longrightarrow} \infty\end{aligned}\)
Remarques
-
Le (c) est absolument central ; dire la minoration \(\circledast\) vient du fait que : \(\forall a, b \in \mathbb{R}, \, \, \left\vert \dfrac{g(a) - g(b)}{a-b}\right\vert \leq 1\) par définition de \(g\) est vrai mais il serait malavisé de passer sous silence ce point (c), puisqu’il sous-tend, entre autres, l’heuristique du choix de \(h_n\) et la vision “géométrique” qui l’accompagne.
-
Le point (c) montre aussi, par contraposée, que si le “grand” intervalle ouvert d’extrémités \(4^n x\) et \(4^n (x + h_n)\) ne contient pas d’entier (ce qui implique que la pente entre \(4^n x\) et \(4^n (x + h_n)\) vaut \(1\) en valeur absolue), alors les “petits” intervalles ouverts d’extrémités \(4^{n-k} x\) et \(4^{n-k} (x + h_n)\) (\(k \in ⟦ 0, n-1 ⟧\)) n’en contiennent pas non plus : cela n’est pas forcément “algorithmiquement” évident, au premier abord. En effet, on peut commettre une erreur de dichotomie, contraire à celle de Zénon d’Élée1, en pensant que des entiers parasites pourraient s’introduire dans les “petits” intervalles, quand bien même il n’y en avait pas dans le “grand”. Cette situation tire son impossibilité du fait que le rapport d’homothétie qui passe du grand intervalle au petit est un inverse d’entier ! C’est donc une raison autant géométrique qu’arithmétique qui est à l’origine du phénomène.
-
-
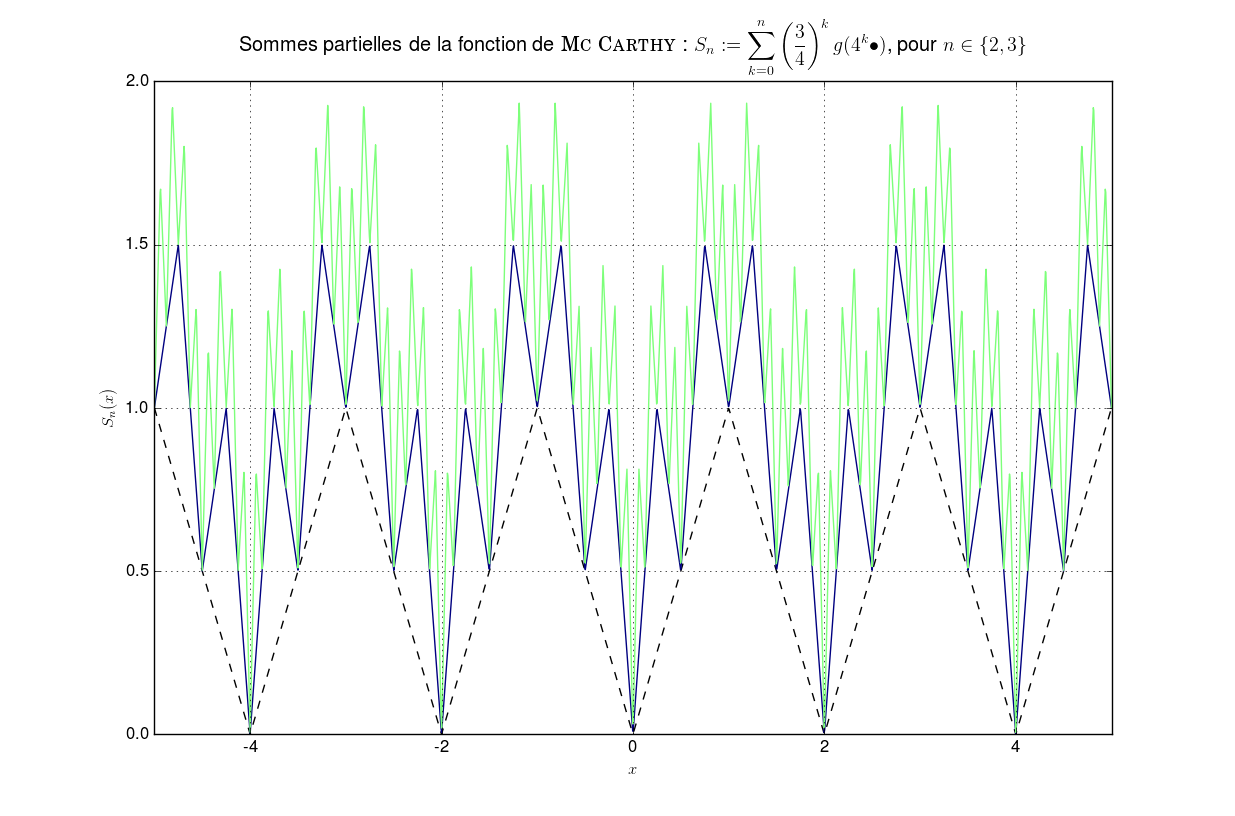
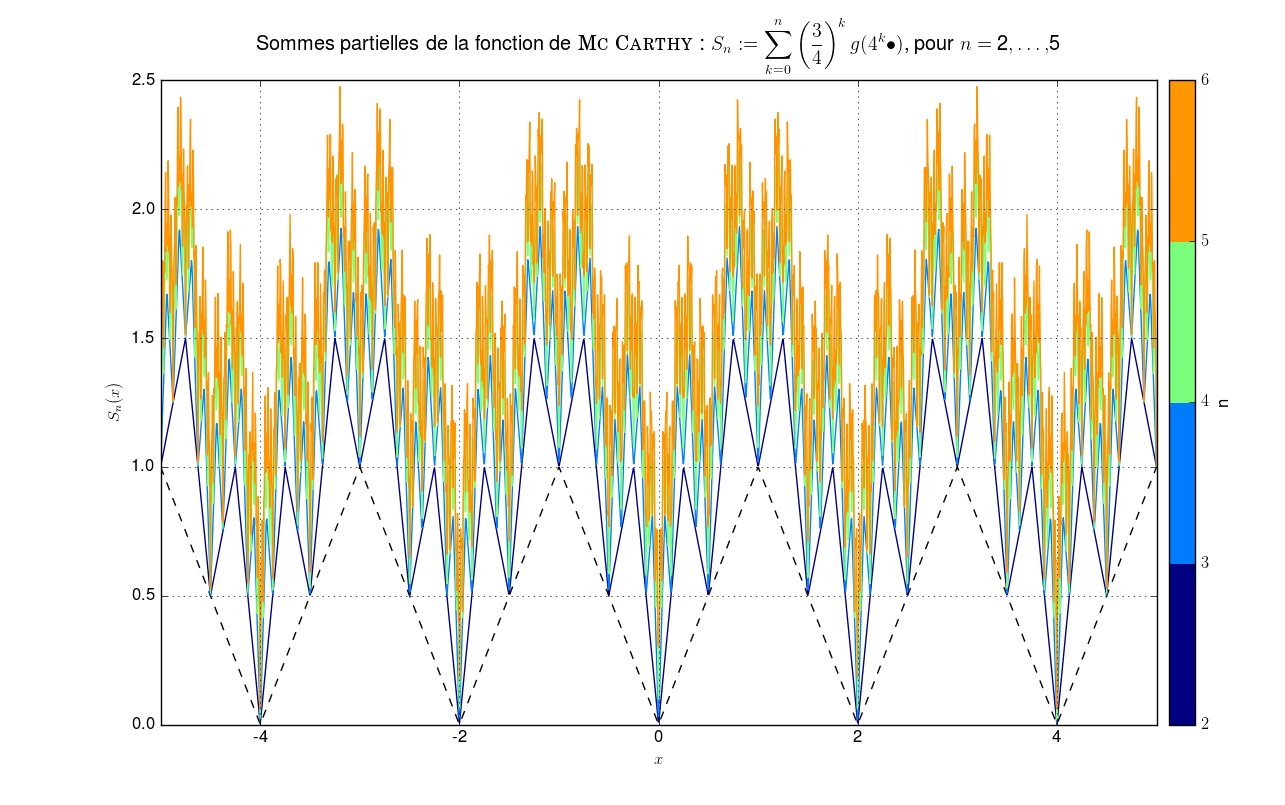
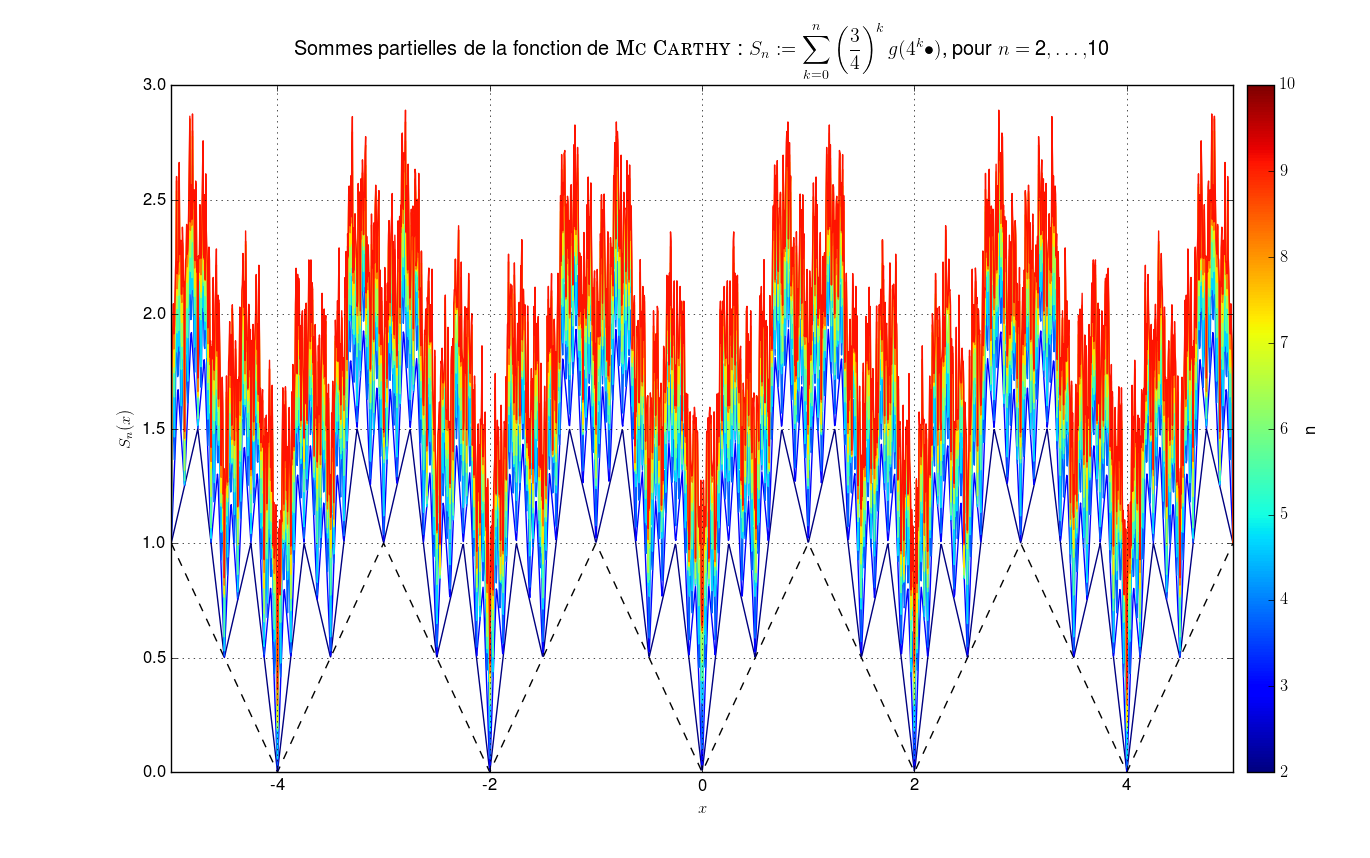
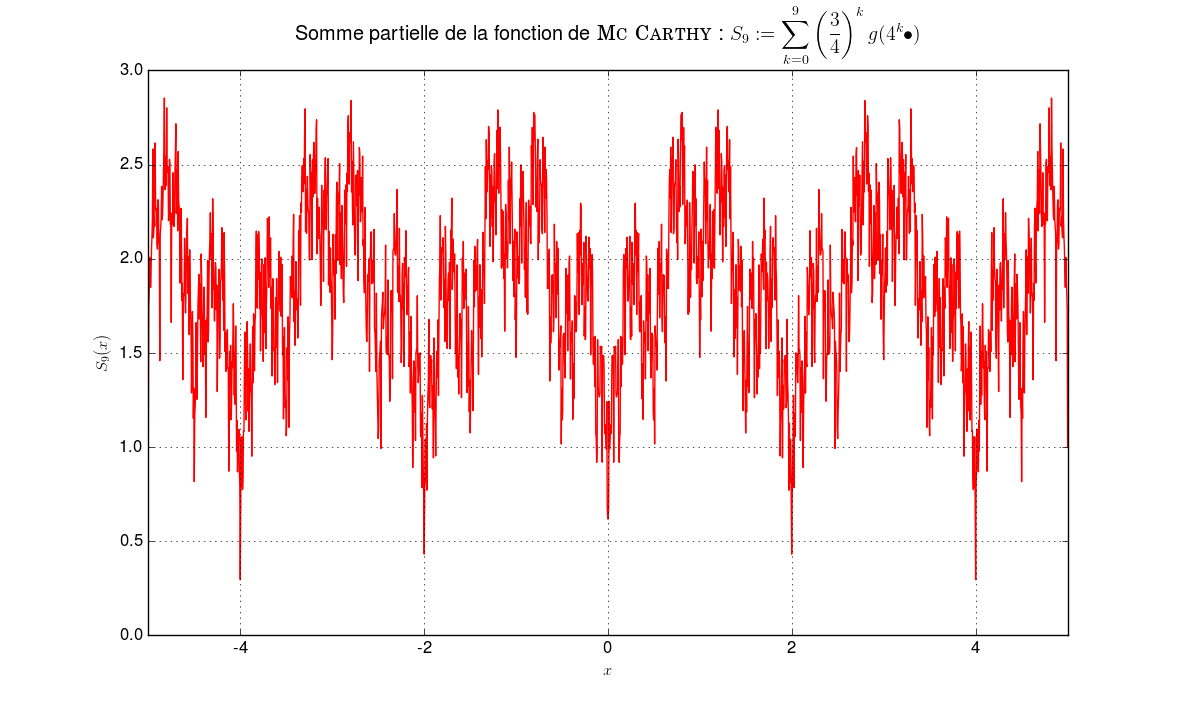
Comparaison avec une série de fonction “similaire” mais dérivableLa différence avec la série de fonctions dérivable2 sur \(\mathbb{R}\) : \(f' {\overset{\small{\text{déf}}}{=}}\displaystyle\sum_{k=0}^n \left(\frac{3}{16}\right)^{k} g(4^k \bullet)\) est flagrante.
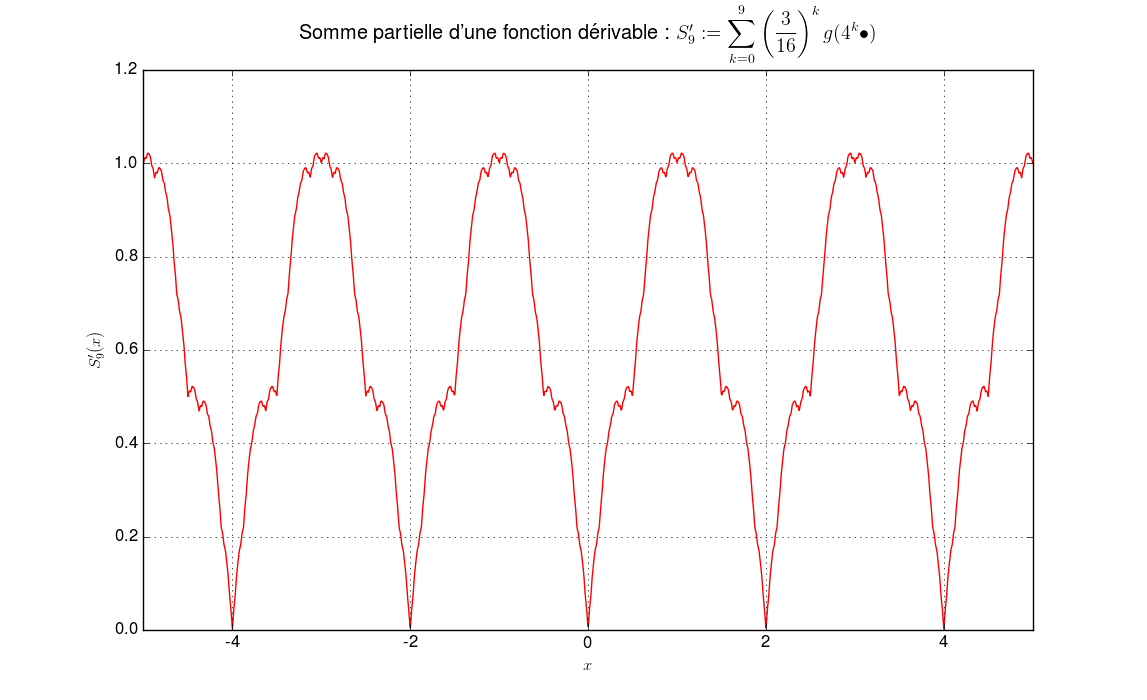
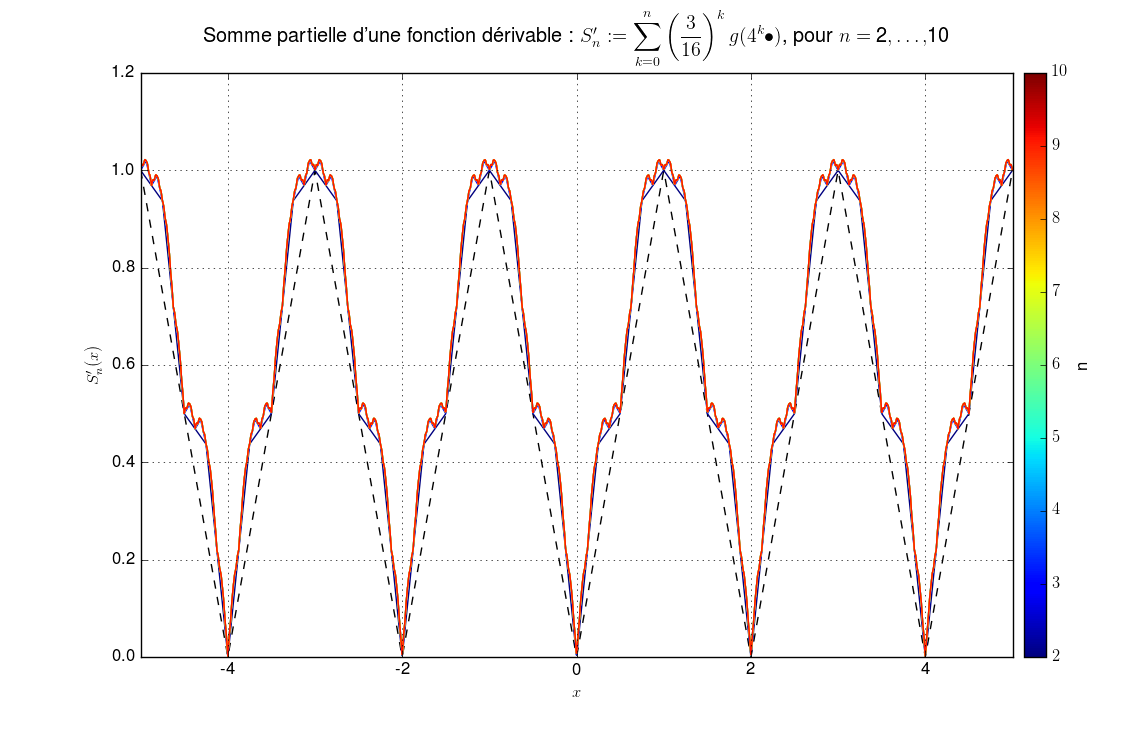
-
par convergence normale ↩

Leave a comment