$$\newcommand{\rec}{\mathop{\rm rec}\nolimits}\newcommand{\ind}{\mathop{\rm ind}\nolimits}\newcommand{\inl}{\mathop{\rm inl}\nolimits}\newcommand{\inr}{\mathop{\rm inr}\nolimits}\newcommand{\Hom}{\mathop{\rm Hom}\nolimits}\newcommand{\Ty}{\mathop{\rm Ty}\nolimits}\newcommand{\Tm}{\mathop{\rm Tm}\nolimits}\newcommand{\op}{\mathop{\rm op}\nolimits}\newcommand{\Set}{\mathop{\rm Set}\nolimits}\newcommand{\CwF}{\mathop{\rm CwF}\nolimits}\newcommand{\CwFB}{\mathop{\rm CwFB}\nolimits}\newcommand{\CwFId}{\mathop{\rm CwFId}\nolimits}\newcommand{\Cat}{\mathop{\rm Cat}\nolimits}\newcommand{\bu}{\bullet}\newcommand{\isContr}{\mathop{\rm isContr}\nolimits}\newcommand{\coh}{\mathop{\bf coh}\nolimits}\newcommand{\id}{\mathop{\rm id}\nolimits}\newcommand{\Id}{\mathop{\rm Id}\nolimits}\newcommand{\refl}{\mathop{\rm refl}\nolimits}\newcommand{\J}{\mathop{\rm J}\nolimits}\newcommand{\scol}{\mathop{\,;\,}\nolimits}$$

Dimensionality Reduction & Visualization of Representations

Younesse Kaddar
Studied articles: Visualizing MNIST, Visualizing Representations (C. Olah), Visualizing Data using t-SNE (L. Van der Maaten & G. Hinton) + Isomap & LLE

Final Summary / Associated Jupyter Notebook

Introduction: Dimensionality reduction

I. MDS, Sammon’s mapping & Force-directed Graph Drawing

II. Principal component analysis (PCA)

III. Isomap

IV. Locally-Linear Embedding (LLE)

V. t-SNE & Meta-SNE

I. Introduction

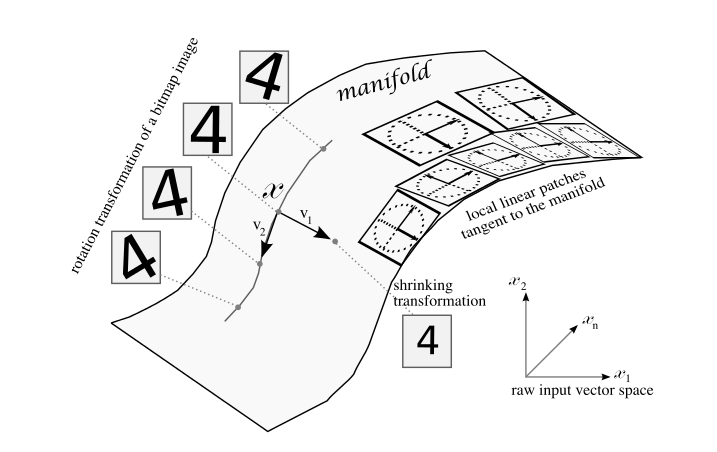
Dimensionality Reduction

high-dimensional data$\qquad \rightsquigarrow \qquad \underbrace{\textit{lower-dimensional data}}_{\text{easier to visualize}}$

Manifold hypothesis: real-world high-dimensional data vectors lie in a lower-dimensional embedded manifold.

Manifold hypothesis

I.A - Multidimensional Scaling (MDS)

Goal: Preserve distances between points ⟹ conserve geometry

Gradient descent to minimize

$$\sum\limits_{x_i ≠ x_j \text{ data points}} \Big(\underbrace{d^\ast(x_i, x_j)}_{\text{dist. in original space}} - \overbrace{d(x_i, x_j)}^{\text{dist. in visualization}}\Big)^2$$

I.B - Sammon’s mapping

The smaller the original distance between points is, the more preserved it is

Cost function to minimize:

$$\sum\limits_{x_i ≠ x_j \text{ data points}} \Big(\frac{d^\ast(x_i, x_j) - d(x_i, x_j)}{d^\ast(x_i, x_j)}\Big)^2$$

I.C - Force-directed Graph Drawing

Build the graph where each point is connected to its $k$ nearest neighbors in original space, then:

Graph Physical analogy
vertices repelling charged particles
edges springs

As with electric potential energy and spring energy, minimize the potential energy function:

$\displaystyle \sum\limits_{x_i ≠ x_j \text{ data points}} \frac{1}{d^\ast(x_i, x_j)}$ $+$ $\displaystyle \sum\limits_{x_i, x_j \text{ data points}} \frac 1 2 \Big(d^\ast(x_i, x_j) - d(x_i, x_j)\Big)^2$

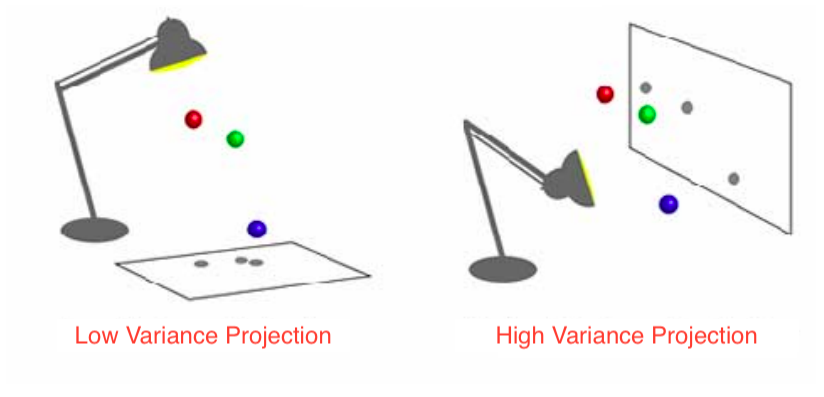
II. Principal component analysis (PCA)

Goal: Find orthogonal axes onto which the variance of the data points under projection is maximal, i.e. find the best possible “angles” from which the data points are the most spread out.

PCA

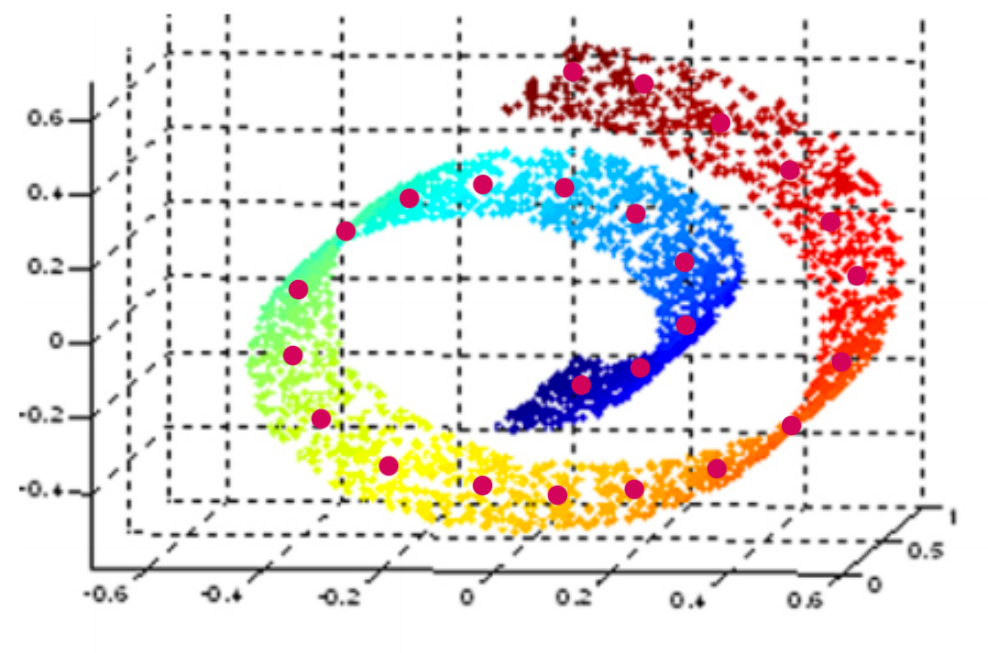
III. Isomap

Goal: MDS but curvature of the data space taken into account

⟶ geodesic distance:
length of paths on curved manifold surfaces are measured as if they were flat
Isomap

IV. Locally-Linear Embedding (LLE)

Goal: Preserve the relationship between neighbors.

  1. Find the weight matrix $(W_{i,j})_{i,j}$ - whose rows sum to $1$ - that minimizes

    $$\sum\limits_{x_i \text{ data point}} \Big\vert \; x_i - \sum\limits_{x_j \text{ neighbor of } x_i} W_{i, j} x_j \;\Big\vert^2$$

  2. Map each data point $x_i$ to a point $y_i$ in the vizualization, s.t. the $y_k$'s minimize

    $$\sum\limits_{y_i \text{ data point}} \Big\vert \; y_i - \sum\limits_{y_j \text{ neighbor of } y_i} W_{i, j} y_j \;\Big\vert^2$$

t-Distributed Stochastic Neighbor Embedding (t-SNE)

the relation "being neighbors"$\qquad \rightsquigarrow \qquad \underbrace{\textit{"continuous range of neighborness"}}_{\text{probability distribution}}$

Map points are:

  • attracted to points that are near them in the data set
  • repelled by points that are far from them in the data set

t-SNE

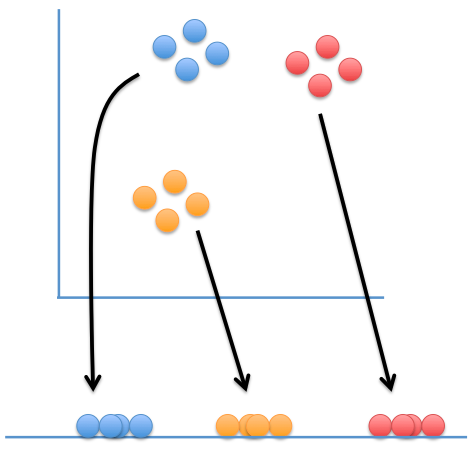
Image courtesy of statquest.org

Step 1

Compute conditional probabilities

$$p_{j\mid i} ≝ \frac{\exp(-\vert\vert x_i-x_j\vert\vert^2/2\sigma^2)}{\sum_{k\neq i}\exp(-\vert\vert x_i-x_k\vert\vert^2/2\sigma^2)}$$

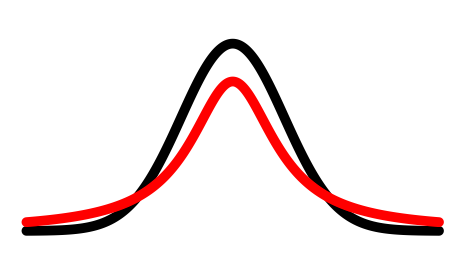
probability that $x_i$ has $x_j$ as its neighbor if neighbors were chosen according to a Gaussian distribution centered at $x_i$


⟶ "similarity" between data points
t-SNE

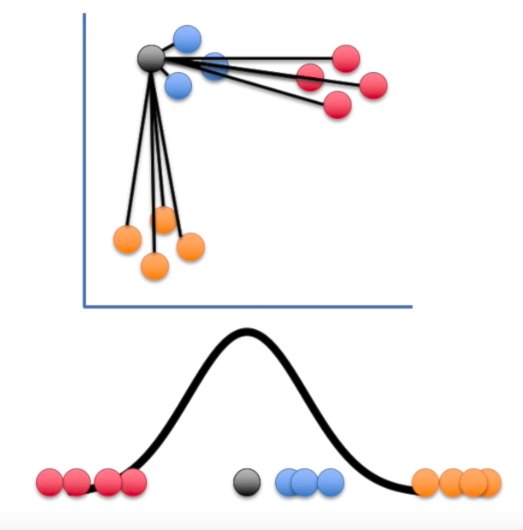
Step 2

Then symmetrize the conditional probabilities:

$$p_{i,j} ≝ \frac{p_{j\mid i} + p_{i\mid j}}{2n}$$

t-SNE t-SNE

Step 3

  • $y_i$'s initialized at random

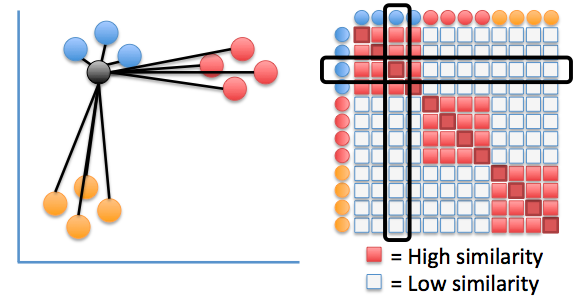
  • Similarities between visualization points:

    $$q_{i,j} ≝ \frac{(1+\vert\vert y_i-y_j\vert\vert^2)^{-1}}{\sum_{k\neq l}(1+\vert\vert y_i-y_l\vert\vert^2)^{-1}}$$

    ⟶ computed with resort to a Student-$t$ distribution


t-SNE
t-SNE

Step 4

  • Minimize the Kullback–Leibler divergence: $C ≝ \sum_{i≠ j}p_{ij}\log {\frac {p_{i,j}}{q_{i,j}}}$, by modifying the $y_i$'s with gradient descent

  • Recompute the $q_{i,j}$'s at each step (until convergence is reached)

t-SNE

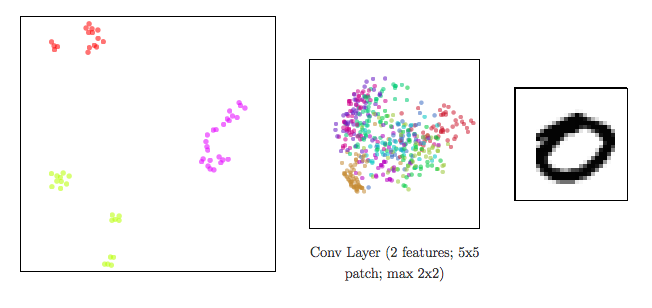
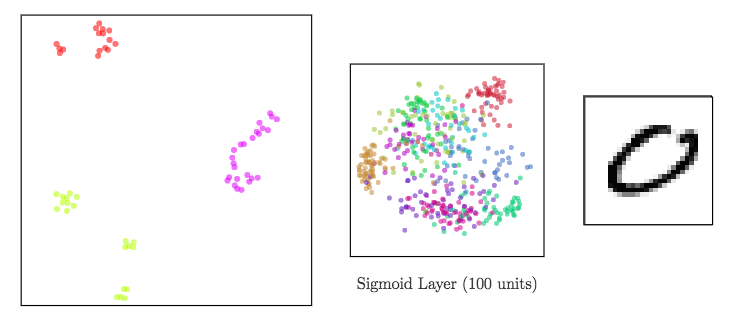
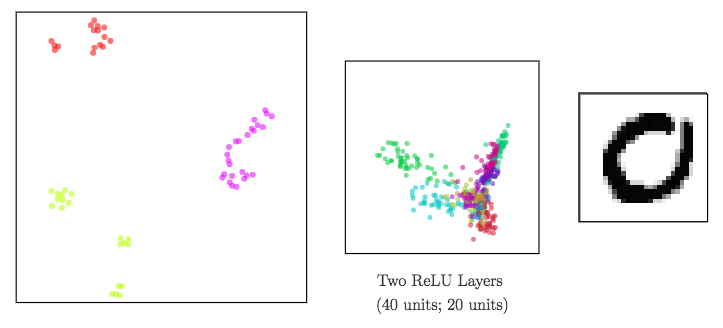
Dimensionality reduction to visualize high-dimensional representations

In a neural network:

  • input data ⟶ shape changed from a layer to another: a representation is the reshaped data at a given layer.
t-SNE

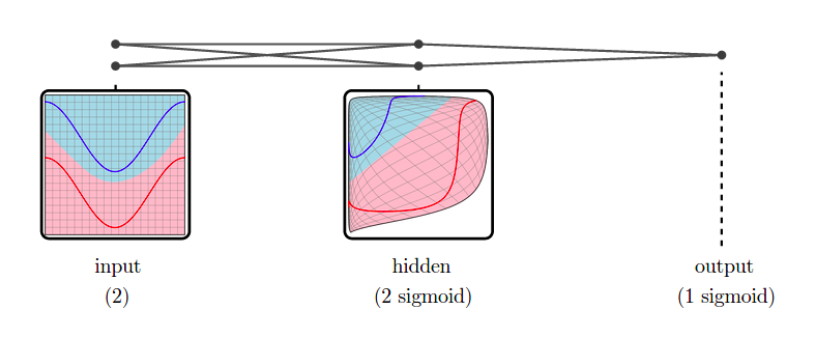
Since representations are high-dimensional ⟹ DR methods to visualize them

meta-SNE to visualize the space of representations

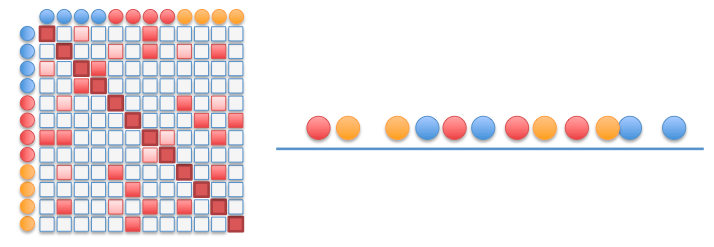
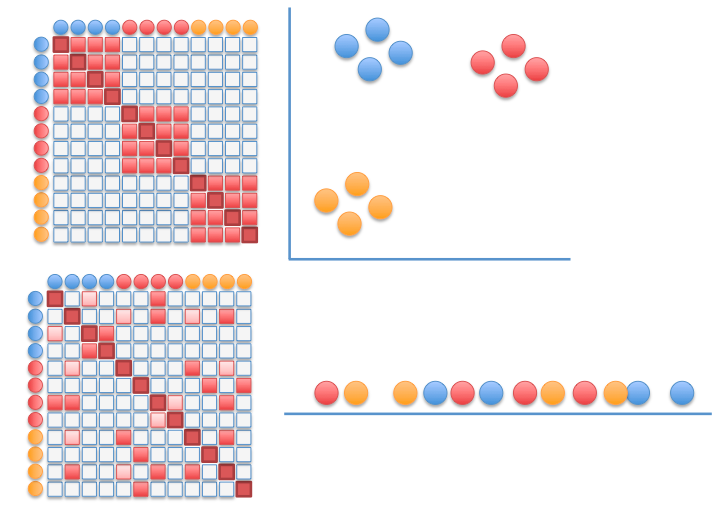
  1. Build matrices of pairwise distances:

    $$D_X ≝ \left(d_X(x_i, x_j)\right)_{i,j}$$
    ⟹ vectorize representations

  2. Step up the ladder of abstraction: visualize vectorized representations with t-SNE

Regarding neural networks: meta-SNE enables us no longer to confine ourselves to comparing their outcome only, but also how they operate internally.

Sigmoid

meta-SNE

ReLU

meta-SNE

CNN

meta-SNE

IV. Conclusion