$λ$-Calculus & Curry-Howard correspondence
Younesse Kaddar
I. $λ$-Calculus
- Definition
- $𝛼$, $𝜂$-conversions and $𝛽$-reduction
- Alligators
II. Fixed-point combinator
- Turing-completeness of $𝜆$-calculus
- Curry and Turing combinators
- Curry-Howard correspondence
I.1 - $λ$-Calculus : definition
Let $𝒱 \; ≝ \; \; \lbrace x, y, z, \ldots \rbrace$ be a fixed set of variables
- $𝛬$ expressions :
-
$$Λ ::=V |Λ Λ |λV·Λ$$the smallest set of functions such that
- $𝒱 \; ⊆ 𝛬$
- Application : $∀u, v∈𝛬, \underbrace{uv}_{\text{interpreted as } u(v)} ∈ 𝛬$
- $𝜆$-abstraction : $∀x∈𝒱, u∈𝛬, \underbrace{𝜆x. u}_{\text{interpreted as } x \mapsto u} ∈ 𝛬$
NB : Such a set exists : apply Knaster-Tarski to the following monotonic function in the complete lattice $𝒫(𝛴^\ast)$, where $𝛴 \; ≝ \; \; \lbrace 𝜆, . \rbrace ∪ 𝒱$
$$\begin{cases} 𝒫(𝛴^\ast) ⟶ 𝒫(𝛴^\ast) \\ 𝛬 \mapsto \lbrace uv \rbrace_{u,v∈𝛬} ∪ \lbrace 𝜆x. u \rbrace_{\substack{x∈𝒱 \\ u∈𝛬}} ∪ 𝒱\end{cases}$$
I.2 - $𝛼$ / $𝜂$-conversions, $𝛽$-reduction
- $𝛼$-conversion :
- $$\lambda x. u= _\alpha \lambda y. (\underbrace{u[x :=y]}_{\rlap{\text{all instances of $x$ in $u$ are replaced by $y$}}})$$
$x=y$ OR $x, y∉ bv(u)$ and $y∉ fv(u)$, as illustrated by these examples :
$(λx·y)[x:=uv] ≠_𝛼 λuv·y$ $(λx·x)[x:=y] ≠_𝛼 λx·y$ $(λy·x)[x:=y] ≠_𝛼 λy·y$ $λx·y[y:=x] ≠_𝛼 λx·x$
- $𝛽$-reduction :
- $$( \lambda x . u ) v \to u [ x := v ]$$
- $𝜂$-conversion :
- $$\underbrace{\lambda x . (u x) =_𝜂 u}_{\rlap{\text{If $x$ does not appear free in $u$}}}$$
Or… in terms of alligators (an idea by Victor Bret)
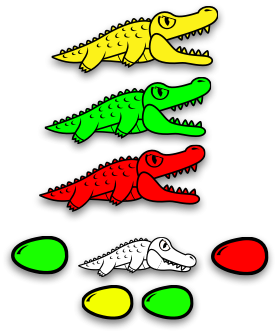
Eating process ≡ $𝛽$-reduction
⇓
⇓
⇓
⇓
⇓
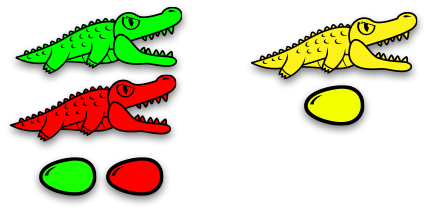
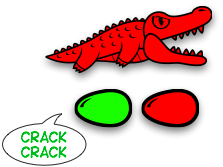
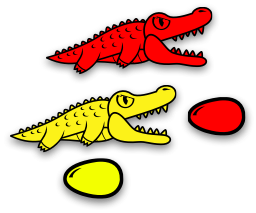
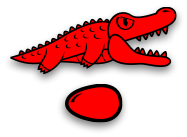
$𝛽$-reduction
⇓
⇓
$𝛼$-conversion
⇓
⇓
old alligators ≡ parentheses
⇓
⇓
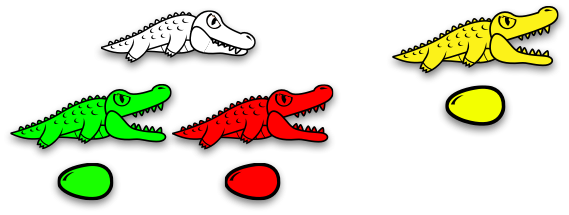
II.1 - Turing-completeness of $𝜆$-calclus
Church Numerals :
$$∀n∈ℕ, \; \lceil n \rceil \; ≝ \; \; 𝜆 f x. f^n(x) \; ⟹ \; ℕ ≃ \left\lbrace 𝜆 f x. f^n(x) \right\rbrace$$
-
Constant function :
$$∀n, k∈ℕ, \; f(x_1,\ldots,x_k) = n \\≡ 𝜆 x_1 ,\ldots, x_k. \lceil n \rceil$$ -
Successor function S :
$$S(x) \stackrel{\mathrm{def}}{=} x + 1 \\≡ 𝜆 n. f(n f x)$$ -
Projection function :
$$P_i^k(x_1,\ldots,x_k) \stackrel{\mathrm{def}}{=} x_i \\≡ 𝜆 x_1 ,\ldots, x_k. \, x_i$$
II.1 - Turing-completeness of $𝜆$-calculus
Operators:
- Composition operator : $𝜆$-abstraction
Now, what about :
- the primitive recursion operator $\rho$ :
$$\begin{align} \rho(g, h) &\stackrel{\mathrm{def}}{=} f \quad\text{where}\\ f(0,x_1,\ldots,x_k) &= g(x_1,\ldots,x_k) \\ f(y+1,x_1,\ldots,x_k) &= h(y,f(y,x_1,\ldots,x_k),x_1,\ldots,x_k)\,.\end{align}$$
- the minimisation operator $\mu$ :
$$\begin{align} \mu(f)(x_1, \ldots, x_k) = z \stackrel{\mathrm{def}}{\iff}\ f(z, x_1, \ldots, x_k)&=0\quad \text{and}\\ f(i, x_1, \ldots, x_k)&>0 \quad \text{for}\quad i=0, \ldots, z-1.\end{align}$$
?
II.1 - Turing-completeness of $𝜆$-calculus
If
$$\mathbf{TRUE} \; ≝ \; \; λx.λy.x \\\mathbf{FALSE} \; ≝ \; \; λx.λy.y$$
then :
$$\mathbf{AND} \; ≝ \; \; λp.λq.p q p \\\mathbf{OR} ≝ λp.λq.p\; p \; q \\\mathbf{NOT} \; ≝ \; \; λp.p \; \mathbf{FALSE} \; \mathbf{TRUE} \\\mathbf{IFTHENELSE} \; ≝ \; \; λp.λa.λb.p \; a \; b \\\mathbf{ISZERO} \; ≝ \; \; λn. \; n \; (λx.\, \mathbf{FALSE}) \; \mathbf{TRUE}$$
But… what about recursion ?
II.2 - Fixed-point combinators
Astounding fact : each $𝜆$-term actually has a fixed point !
and there even exist fixed-point combinators $y$ :
$$\displaystyle y\ f = f\ (y\ f) \ \ \text{ for all } f$$
- The Curry combinator :
- $$\displaystyle Y \; ≝ \; \; \lambda f.(\lambda x.f\ (x\ x))\ (\lambda x.f\ (x\ x))$$
- The Turing combinator :
- $$\displaystyle 𝛳 \; ≝ \; \; \big(λf. λg. \, g \, (f \, f \, g) \big) \big(λf. λg. \, g \, (f \, f \, g)\big)$$
$$\begin{align*} Y\ f & = (\lambda f'.(\lambda x.f'\ (x\ x))\ (\lambda x.f'\ (x\ x)))\ f \\ & = (\lambda x.f\ (x\ x))\ (\lambda x.f\ (x\ x)) \\ & = f (\underbrace{(\lambda x.f\ (x\ x))\ (\lambda x.f\ (x\ x))}_{= Y\ f})\end{align*}$$
$$fact \; n = \begin{cases} 1 \text{ if } n=0 \\ n × (fact \, (n-1)) \text{ else}\end{cases}$$
$$F f \; ≝ \; \; 𝜆f. n \, (𝜆x. \, n × f (Pred \, n)) \, 1 \\Succ \, n \; ≝ \; \; 𝜆n f x. f(n f x) \\Pred \, n \; ≝ \; \; 𝜆n. 𝜋_1 \Big( n \, \big(𝜆c. ⟨𝜋_2 c, Succ \, 𝜋_2 c⟩\big) \, ⟨0,0⟩ \Big) \\n × m \; ≝ \; \; 𝜆n, m. n (m f)$$
$$\begin{align*} fact & = YF \\ & = 𝜆f. (𝜆x. f (xx)) (𝜆x. f (xx)) \Bigg( 𝜆f. n \, \Big(𝜆x. \, n × f \Big(𝜋_1 \\ &\bigg( n \, \big(𝜆c. ⟨𝜋_2 c, Succ \, 𝜋_2 c⟩\big) \, ⟨0,0⟩ \bigg) \Big)\Big) \, 1 \Bigg) \\\end{align*}$$
II.3 - Curry-Howard isomorphism
It’s great, but… you can’t do that in Haskell (for example) :
y :: (a -> a) -> a y = \f -> (\x -> f (x x)) (\x -> f (x x))
⇓
Occurs check: cannot construct the infinite type: r0 ~ r0 -> t
Expected type: r0 -> t
Actual type: (r0 -> t) -> t
Because Haskell (and other functional programming languages such as OCaml, Lisp, Clojure, etc…) is strongly typed.
- What is a type ? :
- A type is a property of a program.
Ex :
- the type of the $𝜆$-term $\lceil 1 \rceil$ can be be thought as "Integer" :
int. - the program $fact$ takes a natural number and produces
another natural number : its type is $int ⟶ int$
The CURRY-HOWARD CORRESPONDENCE :
Proofs can be represented as programs ($𝜆$-terms), and the formulas it prove are the types for the program
| Intuitionistic implicational natural deduction | Lambda calculus type assignment rules |
|---|---|
$$\displaystyle \frac{}{\Gamma_1, \alpha, \Gamma_2 \vdash \alpha} \text{Ax}$$ |
$$\displaystyle \frac{}{\Gamma_1, x:\alpha, \Gamma_2 \vdash x:\alpha}$$ |
$$\displaystyle\frac{\Gamma, \alpha \vdash \beta}{\Gamma \vdash \alpha \rightarrow \beta} \rightarrow I$$ |
$$\displaystyle\frac{\Gamma, x:\alpha \vdash t:\beta}{\Gamma \vdash \lambda x.t : \alpha \rightarrow \beta}$$ |
$$\displaystyle\frac{\Gamma \vdash \alpha \rightarrow \beta \qquad \Gamma \vdash \alpha}{\Gamma \vdash \beta} \rightarrow E$$ |
$$\displaystyle\frac{\Gamma \vdash t:\alpha \rightarrow \beta \qquad \Gamma \vdash u:\alpha}{\Gamma \vdash t\;u:\beta}$$ |
From a logical standpoint, the $Y$ combinator corresponds to the Curry paradox.
“If this sentence is true then I am an alligator” is true : why ?
Let’s suppose that the sentence is true : it must be shown that I am an alligator.
But since the sentence is true, modus ponens can be applied, which yields the conclusion.
1
$λ$-Calculus & Curry-Howard correspondence
Younesse Kaddar
I. $λ$-Calculus
Definition
$𝛼$, $𝜂$-conversions and $𝛽$-reduction
Alligators
II. Fixed-point combinator
Turing-completeness of $𝜆$-calculus
Curry and Turing combinators
Curry-Howard correspondence