$∞$ Infinity $∞$
Younesse Kaddar
I. What is it that we call infinity ?
- Zeno’s Paradoxes
- Hilbert’s Hotel
II. How big is it ?
- Counting to $∞$ : $\aleph_0$
- Ordinals : $𝜔$
- Inaccessible cardinals
Zeno’s paradoxes
Zeno of Elea : In a race, the quickest runner can
never overtakethe slowest.


$⇑$
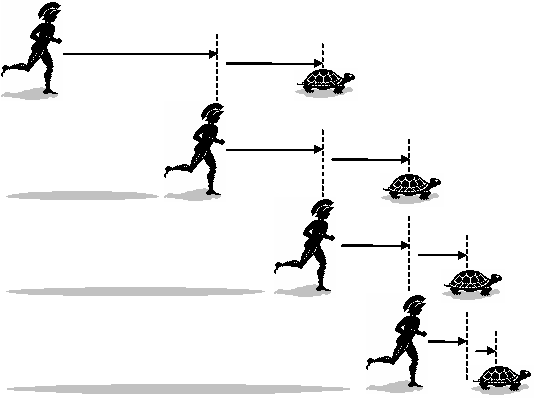

Actually, modern math provide a solution :
$$\sum_{n>0} \frac{1}{2^n}$$ is convergent
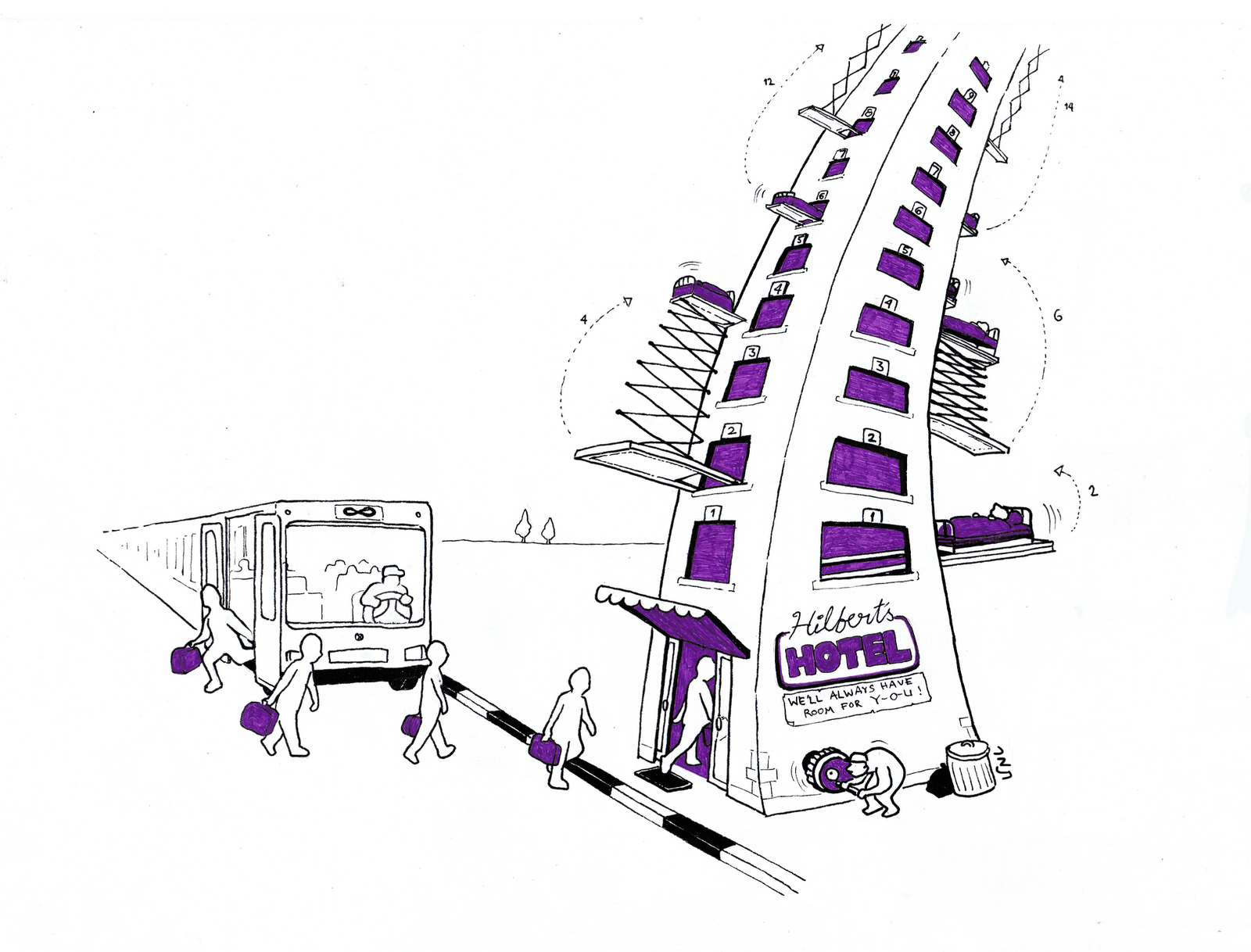
Hilbert's Hotel
- Fully occupied
- Infinitely many rooms
$⟶$ How many additional guests can be housed ?
- For $n$ new guests : a shift of $n$
- How about infintely many new guests ?
II. How big is infinity ?
Cardinals : $\aleph_0$
Cardinal : the number of elements of an unordered set
$\downarrow$
NB : Zeno paradox ⟹ $\aleph_0$ elements can be "written" within a finite space
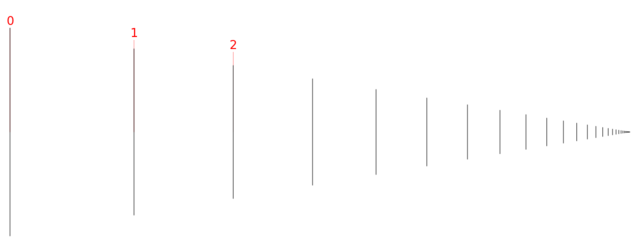
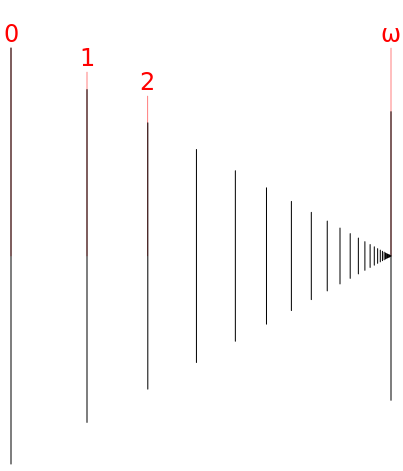
Ordinals : $𝜔$
Ordinal : the first label you’ll have to use in order to append 1 element to an ordered set
NB :
- For a finite number of elements : ordinal ⟺ cardinal
- $\aleph_0 + 1 = \aleph_0$, but $𝜔 + 1 \neq 𝜔$
Axiom of replacement : to infinity and beyond !
Axiom of replacement : if you take an existing set and replace all elements with something else, you’re left with an other existing set.
We’re going to use it to the fullest !
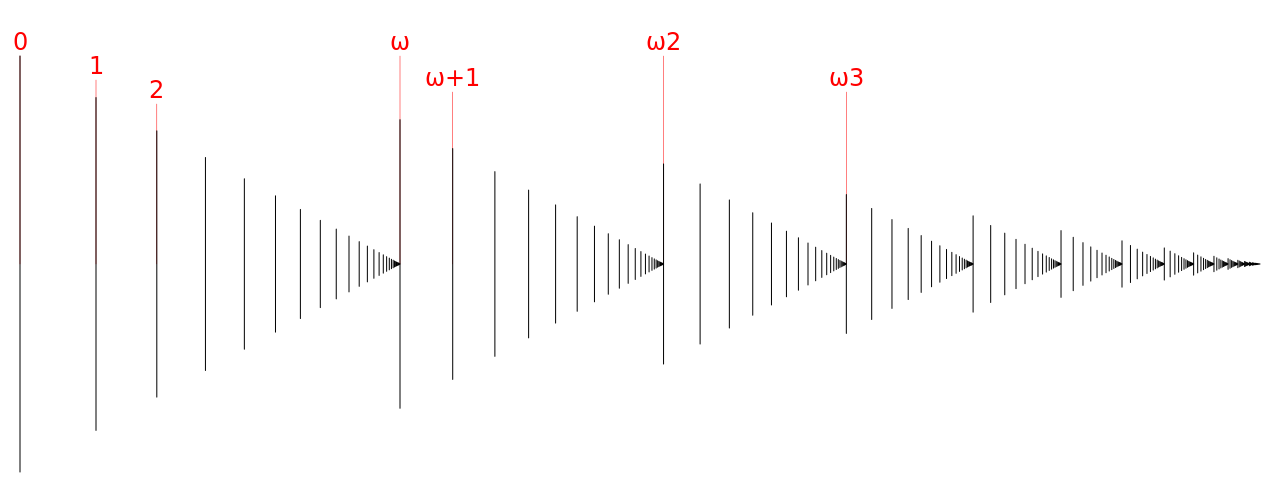
$𝜔^3$
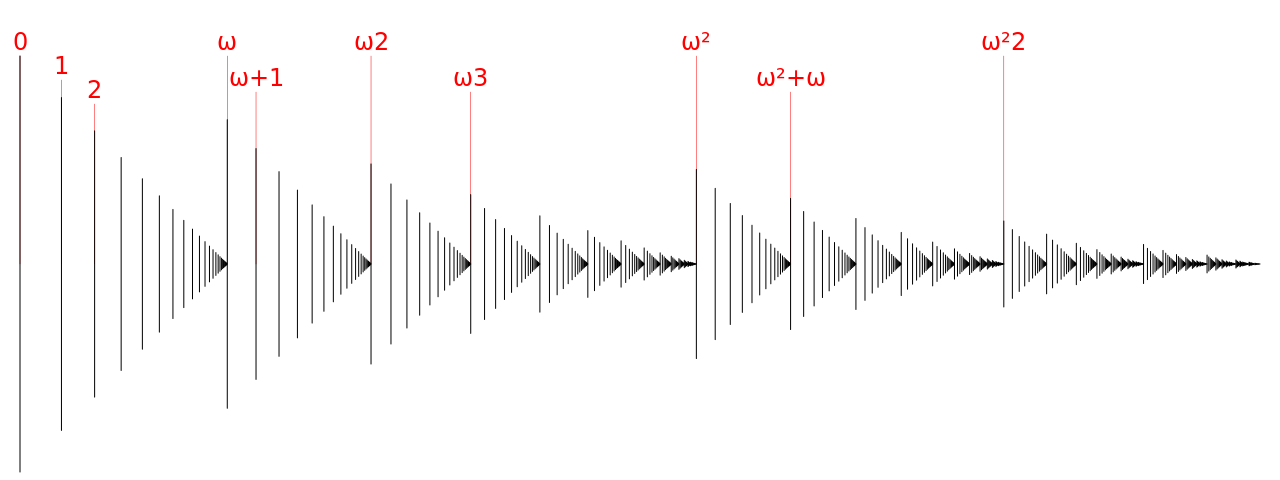
$𝜔^4$

$𝜔^𝜔$

$𝜔^{5}$

$𝜔^{𝜔^𝜔}$

$𝜔^{𝜔^{𝜔^{\vdots^{𝜔}}}}$
up to
$𝜀_0$
And all that is smaller than …
$\omega_1$
corresponding to the cardinal …
$\aleph_1$
Then …
$𝜔_2, 𝜔_3, \ldots, 𝜔_{𝜔}, \ldots, 𝜔_{𝜔^{𝜔^{𝜔^{\vdots^{𝜔}}}}}, 𝜔_{𝜀_0}, \ldots$
and the corresponding cardinals
$\aleph_2, \aleph_3, \ldots$
Power sets : becoming exponentially big
$|𝒫(E)| = 2^{|E|}$
+Axiom of replacement
$\downarrow$
We iterate over and over both operations !
But all of that has an order type … so : it remains smaller than …
Inaccessible cardinals