TD7 : Adéquation, Théorèmes du point fixe, DCPO

1.

1.

a)

$𝜌\vdash x ⟹ 𝜌(x)$

$𝜌\vdash \dot{n} ⟹ n$

$𝜌\vdash e ⟹ n$	$𝜌\vdash e’ ⟹ n’$
$𝜌\vdash e\dot{+}e’ ⟹ n + n’$

$𝜌\vdash e ⟹ n$
$𝜌\vdash \dot{-}e ⟹ -n$

$𝜌\vdash e ⟹ n$
$𝜌\vdash \dot{f}(e) ⟹ f(e)$	si $n∈Dom(f)$

b).

\[⟦⟧ : Env ⟶ ℤ_{\bot}\] \[⟦x:=e⟧𝜌 = 𝜌[x \mapsto ⟦e⟧𝜌] \\ ⟦skip⟧𝜌 = 𝜌 \\ ⟦while \, \, e \, \, do \, \, c⟧𝜌 = \begin{cases} ⟦while \, \, e \, \, do \, \, c⟧(⟦c⟧𝜌) \text{ si } ⟦e⟧𝜌 ≠ 0 \\ 𝜌 \end{cases} \\ ⟦if \, \, e \, \, then \, \, c_1 \, \, else \, \, c_2⟧𝜌 = \begin{cases} 𝜌(⟦c_1⟧𝜌) \text{ si } ⟦e⟧𝜌 ≠ 0 \\ 𝜌(⟦c_2⟧𝜌) \text{ sinon }\\ \end{cases}\]

De plus :

\[⟦x⟧𝜌 = 𝜌(x) \\ ⟦\dot{n}⟧𝜌 = n\\ ⟦e \dot{+} e'⟧𝜌 = ⟦e⟧𝜌 + ⟦e'⟧𝜌 \\ ⟦\dot{-} e⟧𝜌 = -⟦e⟧𝜌\\ ⟦f(e)⟧𝜌 = \begin{cases} f(⟦e⟧𝜌) \text{ si } ⟦e⟧𝜌∈Dom(f) \\ \bot \, \text{ sinon } \end{cases}\]

c).

$𝜌 \vdash e ⟹ n$ ssi $⟦e⟧𝜌 = n$

Double implication, par induction.

d).

Le dénotationnel est bien plus pratique et élégant, et dans le cas des expressions arithmétiques, il y a toujours terminaison (contrairement au cas général des programmes), donc on préfère l’utiliser.

2).

a).

Sémantique opérationnelle :

$𝜌\vdash x ⟹ 𝜌(x)$

$𝜌\vdash \dot{n} ⟹ n, 𝜌$

$𝜌\vdash e_1 ⟹ n_1, 𝜌_1$	$𝜌_1 \vdash e_2 ⟹ n_2, 𝜌_2$
$𝜌\vdash e_1 \dot{+} e_2 ⟹ n_1 + n_2, 𝜌_2$

$𝜌\vdash e ⟹ n, 𝜌’$
$𝜌\vdash \dot{-} e ⟹ -n, 𝜌’$

$𝜌\vdash c ⟹ 𝜌’$	$𝜌’ \vdash e ⟹ n, 𝜌’’$
$𝜌\vdash c \text{ resultis } e ⟹ n, 𝜌’’$

Sémantique dénotationnelle :

\[⟦⟧ : Env ⟶ ℤ_{\bot}\] \[⟦x⟧𝜌 = 𝜌(x), 𝜌 \\ ⟦\dot{n}⟧𝜌 = n, 𝜌 \\ ⟦e \dot{+} e'⟧𝜌 = fst(⟦e⟧𝜌) + fst(⟦e'⟧snd(⟦e⟧𝜌)) \\\]

c’est beaucoup moins satisfaisant, maintenant.

b).

L’addition n’est plus commutative : cela dépend de la sémantique, qui stipule - en l’occurrence - que c’est la première expression qui est évaluée.

5.

1.

Montrons que l’ensemble des points fixes $Fix(f)$ est un treillis complet.

Si $A ⊆ Fix(f)$, montrons que $a_0 ≝ \sup_{A’ ⊆ Fix(f)}(\inf(A’; A⊆A’))$ est un point fixe.

\[a_0 ≤ a, ∀a∈A \\ ⟹ f(a_0) ≤ a, ∀a∈A\]

donc $f(a_0)$ minore $A$ et \(f(a_0)≤a_0\)

De plus :

$a_0 ≥ a’, ∀a’ ∈ {\inf(A’; A⊆A’)}_{A’ ⊆ Fix(f)}$

donc

$f(a_0) ≥ f(a’)=a’, ∀a’ ∈ {\inf(A’; A⊆A’)}_{A’ ⊆ Fix(f)}$

M2 :

$w ≝ \sup_X (A)$

Considérer $f: [w, T]⟶X$

• $f$ croît
• $[w, T]$ treillis complet
• $f([w, T]) ⊆ [w, T]$

Soit $x∈[w, T]$,

$f(x)≤T$

\[\Big( ∀a∈A, a≤w≤x ⟹ f(a)=a≤f(x) \Big) ⟹ A ≤ f(x) \\ ⟹ w ≤ f(x)\]

Knaster-Tarski ⟶ $f$ admet un plus petit point fixe $x_0$ dans $[w,T]$.

• maj : $∀a∈A, a≤w≤x_0$
• sup : $∀y ∈ Fix(f), A ≤ y ⟹ w ≤ y$ donc $x_0≤y$

2) Cantor Bernstein :

En posant $E=A$, $F=B$.

$f: E⟶F$ et $g: F⟶E$ injectives.

On pose \(H ≝ \begin{cases} 𝒫(E) ⟶ 𝒫(E) \\ X \mapsto E\backslash g(F\backslash f(X)) \end{cases}\)

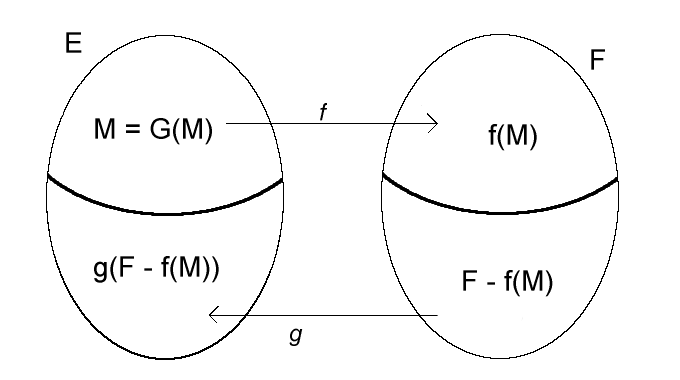
($H = G$ sur ce dessin)

1) Mq $H$ est monotone.

Soient $X, Y ⊆ E$ tq $X⊆Y$.

\[\begin{align*} X⊆Y &⟹ f(X) ⊆ f(Y) \\ &⟹ F\backslash f(Y) ⊆ F\backslash f(X) \\ &⟹ g(F\backslash f(Y)) ⊆ g(F\backslash f(X)) \\ &⟹ H(X) = E\backslash g(F\backslash f(X)) ⊆ H(Y) = E\backslash g(F\backslash f(Y)) \end{align*}\]

Par le th de Knaster-Tarski, $H$ admet un point fixe $Z$.

\[Z = H(Z) = E\backslash g(F\backslash f(Z)) \\ ⟹ E\backslash Z = g(F\backslash f(Z))\]

On définit \(h ≝ \begin{cases} E ⟶ F \\ x \mapsto \begin{cases} f(x) \text{ si } x∈Z \\ g^{-1}(x) \text{ sinon. } \end{cases} \end{cases}\)

NB : Comme $E\backslash Z = g(F\backslash f(Z))$, si $x \not ∈ Z$, $∃u ∈ F\backslash f(Z); x = g(u)$, et $u$ est unique par injectivité de $g$.

Mq $h$ est injective :

Si $x,y ∈E; h(x) = h(y)$.

• Si $x, y∈Z$ : $x=y$ par injectivité de $f$
• Si $x, y\not∈Z$ : $x,y$ ont le même antécédent par $g$, donc $x=y$
• Si $x∈Z, y\not∈Z$ : $h(x) = f(x) ∈ f(Z)$, $h(y) = g^{-1}(y) ∈ F\backslash f(Z)$, donc $h(x) \neq h(y)$.

Mq $h$ est surjective :

Soit $y ∈ F$.

• Si $y ∈ f(Z), ∃ z ∈ Z; y = f(z)$, et $y = f(z) = h(z)$
• Si $y \not∈ f(Z), y = g^{-1}(g(y)) = h(g(y))$

5.