[Problem Set 3 Spike trains] Problem 2: Analysis of spike trains

Link of the iPython notebook for the code

AT2 – Neuromodeling: Problem set #3 SPIKE TRAINS

PROBLEM 2: Analysis of spike train

One records and analyses several spike trains from a single neuron in the primary somatosensory cortex of a monkey experiencing a vibratory stimulus on the fingertip, for different vibration frequencies $f_1 ∈ \lbrace 8.4, 12, 15.7, 19.6, 23.6, 25.9, 27.7, 35\rbrace \text{ Hz}$. The simulation is conducted between $200$ and $700$ msec.

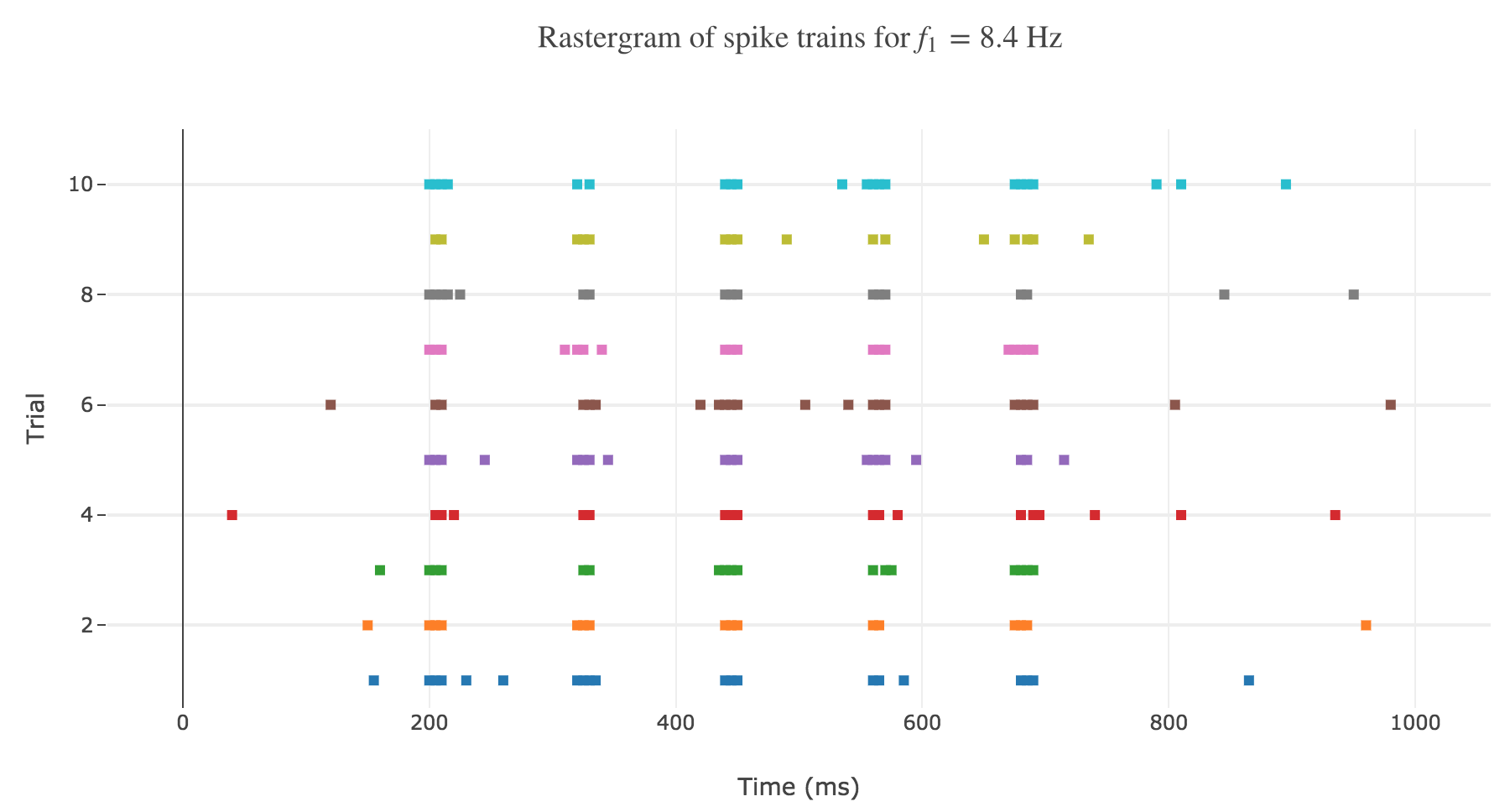
Figure
Figure a. - Rastergram of the spike trains for the first $8.4$ Hz vibration frequency
Figure
Figure b. - Rastergram of the spike trains for various vibration frequencies

As shown in Figure a. and Figure b., the spikes within the simulation period (between $200$ and $700$ msec):

  • seem to be periodically spaced for a given frequency $f_1$
  • are more and more numerous as the frequency increases

and even more: the number of spikes seem to depend linearly on the vibration frequency.

The latter observation is backed up by the shape of the average spike count, plotted as a function of the vibration frequency:

Figure
Figure c.1. - Average spike count as a function of the vibration frequency with standard deviation errorbars

A linear regression of the average spike counts (as a function of the vibration frequency) can me made:

  • Linear equation: \(y = 1.39 x + 3.08\)
  • Correlation coefficient: $0.997$
  • Standard error of the estimate: $0.04$

The very high correlation coefficient and very low standard error of the estimate highlight an almost perfect match!

We have similar results for the average firing rate as a function of the vibration frequency:

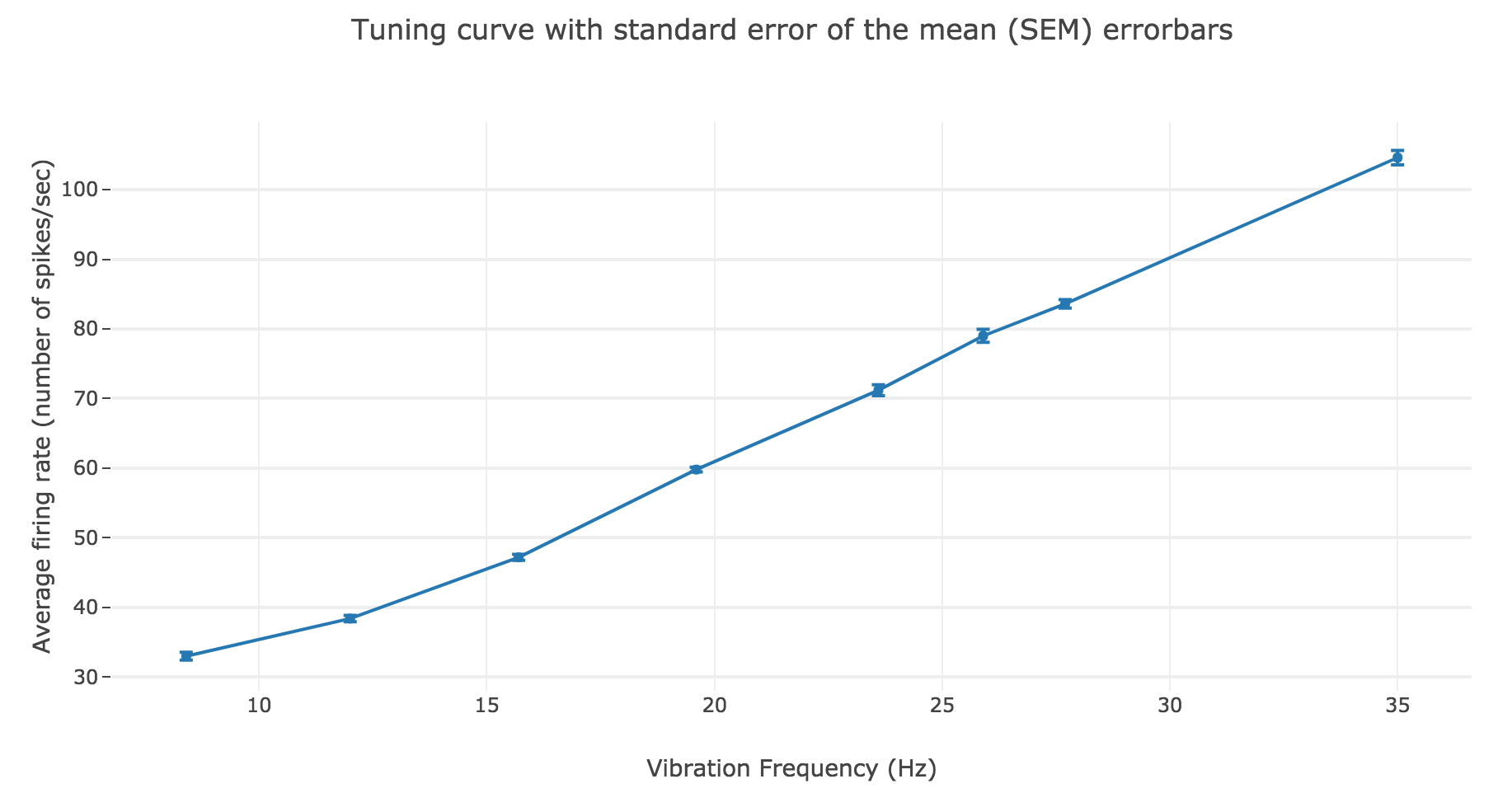
Figure
Figure c.2. - Average firing rate as a function of the vibration frequency with standard error of the mean $SEM = σ/ \sqrt{N}$ errorbars

The linear regression yields:

  • Linear equation: \(y = 2.78 x + 6.15\)
  • Correlation coefficient: $0.997$
  • Standard error of the estimate: $0.08$

As a result: the firing rate of the neuron can be regarded as a non-decreasing linear function of the vibration frequency.

Leave a comment