Lecture 7: Motor Control
Teacher: Emmanuel Guigon (ISIR, Sorbonne Université)
Motor control ⟶ nothing is nominal, not only reaction time to take into account, also motor responses
First, define actions:
- Actions:
-
driven by goals (different from reflex, which is not goal-directed), and they can reach these goals or fail to do so
Actions involve:
- volitional control: you always have some kind of control over it
- Planning
- Predictions, anticipation of outcome
-
Sometimes: agency ⟶ consciousness involved (when actions are prefomed automatically, by habit: no agency)
- more than 70% of our daily actions: classified as automatic
Motor control: not often associated with cognition
Example: playing chess:
- the problem of finding the best next move ⟶ we can tackle it computationally
- moving the pieces on a chessboard: a child is better than the state-of-the-art robots
Cognition is action
Cognition is action: thinking as accompanied with a sequence of actions
- cognition ⟶ generates structure by action
- the cognitive agent is immersed in his/her task domain
- system states ⟶ acquire meaning in the context of action
- cognitive systems are thought to be inseparable from embodiment
- models of cognition take into account the embedded and ‘extended’ nature of cogntive systems
Rapid responses ‘reflexes’ (ex: reacting to hot water) < Rythmic (automatic) movements (ex: walking) < Voluntary movements (ex: speaking)
Important aspect of actions: there is a content (ex: when you take your keys, you need to exert a force on them, which you can measure) ⟶ each action has:
- a specific direction (left/right, toward/away)
- an intensity (velocity, force, …)
⟶ anticipatory electrical activities (EEG, EMG, etc…)
What actions reflect
Action reflects decision
Decision task: the agent has to say if a presented word is an English word or not a lexical word ⟶ experimentally, agents react faster when they see a known word than a non-word.
Action reflects motivation
Task: the subject press a ball as strongly as possible. Meanwhile, stimuli are presented in a subliminal way:
- Priming: some of them are associated to power, force, etc…
- Control: some of them are not
- Priming + Reward: the strength-related stimuli are accompanied with positive reinforcemeent
⟹ Strength of the subject: Priming + Reward > Priming > Control
Action reflects decision making
Experiment: two species of monkeys have to choose between one banana close to them, or three bananas further away
- Marmosets: the further the three bananas, the less likely they are to head to them
- Tamarins: insensitive to the distance to the three bananas ⟶ they always seek them
Organization of action
Neural commands → Muscle Activation → Joint motions → Hand trajectories → Task goals
Lexicon
- Kinematics:
-
position, velocity, acceleration in task/body space
- Dynamics:
-
force/torque (Newton’s law)
- Degrees of freedom:
-
«the least number of independent coordinates required to specify the position of the system elements without violating any geometrical constraints. » Saltzmann (1979)
Redundancy
Degrees of freedom ⟶ problem of redundancy: in task space, when you have so many degrees of freedom than you can choose different trajectories
Muscle redundancy: more muscles than necessary to exert a given force
Is redundancy a problem or a benefit? ⟶ in terms of motor coordination, it is good to have many solutions to solve a given task
Noise
There is noise at all stages of sensorimotor processing (sensory, cellular, synaptic, motor)
Standard deviation increases as the instructed force does ⟶ the higher the force, the more noise there is.
Signal-dependent noise: the noise increases with the signal level
Delays
« We live in the past »: we see/account for something, it has already happened ⟶ we need to take into account these delays
When you exert a force ⟶ have to wait a certain delay before the force reaches its maximum level
EMG of stretched muscle: several response phases:
- spinal propriorecptive feedback
- cortical propriorecptive feedback
- visual feedback
Motor invariants
- Trajectories:
-
point-to-point movements are straight with bell-shaped velocity profiles
⟶ properties in external spaces that are invariant tto the body position
- Motor equivalence:
-
actions are encoded in the central nervous system in terms that are more abstract than commands to specific muscles
⟶ there invariant respresentations of writing for instance: you can write with your hands, foot, teeth, etc… ⇒ same shape
- Scaling laws:
-
duration and velocity scale with amplitude and load
⟶ intertia in certain positions ⇒ slower movements
EMG: Triphasic patterns during fast movements: agonist muscle, then antagonist, then again agonist.
Commands sent even if the arm cannot move: you can measure that the command is the same irrespective of whether the arm is blocked or not (with EMG)
Uncontrolled manifold, structured variability: « Repetition without repetition » (Berstein)
Structured variability: each you reproduce a movement, you perform a (slightly) different movement
Ex: the subject has to do movement, going through points ⟶ variability accumulates (standard deviation of the trajectories) at positions where it is not necessary to be precise, whereas it is made minimal at specific strategic points
Are motor invariant really invariants or simply by-products of control?
Motor variability is as important as motor invariants (structure of variability).
Flexibility & Law of movement
If you disturb the movement at some point, the controller can go back to the intended trajectory. Motor control is highly flexible in space and time.
Laws of movements
Fitt’s law
Speed/accuracy trade-off: going back and forth over a $w$-wide target. $A$: amplitude of the movement. $MT$: movement time, $a, b$: constants
\[MT = a + b \log_2(2A/w)\]Computational motor control
Descriptive (mechanistic) vs. normative models
-
Descriptive: how the world is (action characteristics stem from properties of synapses, neurons, ….)
-
Normative: how the world should be (action characteristics result from principles, overarching goals)
Dynamical system theory: describe behavior in space/time of complex, coupled systems.
- State variables:
-
the smallest possible subset of system variables that can represent the entire state of the system at any given time.
- $x[n]$: state
-
$y[n]$: output (observation)
- ex: if the state is the temperature, $y$ can be the output of a thermometer
-
$u[n]$: input (control)
- output equation: \(\begin{cases} y[n] = g(x[n]) \\ y[n+1] = h(x[n], u[n]) \end{cases}\)
Control theory: deals with the behavior of dynamical systems, and how their behavior can be modified by feedback.
- Open-loop (feedforward):
-
the controller is an inverse model of the system
reference ⟶ Controller ⟶ input (+noise, perturbations) ⟶ System ⟶ state
- Closed-loop (feedback):
-
the controller is a function of an error signal
reference ⟶ Controller ⟶ input ⟶ System ⟶ state ⟶ Observation ⟶ output ⟶ Controller ⟶ ⋯
Internal models
Direct (forward) model: predicts the behavior of the system (ex: when I move my arm, I can try to predict the displacement) ⟶ causal: from the control to the effect
Inverse model: for the desired effect to the control (ill-defined model: many possible solutions)
Forward models
Use of a direct model (rather than external feedfback) to evaluate the effect of command and associated error ⟶ avoid delays in feedback loops (triggering instability).

Kalman filter
Combines forward model and state observation to obtain the best state prediction (there are delays and noise)
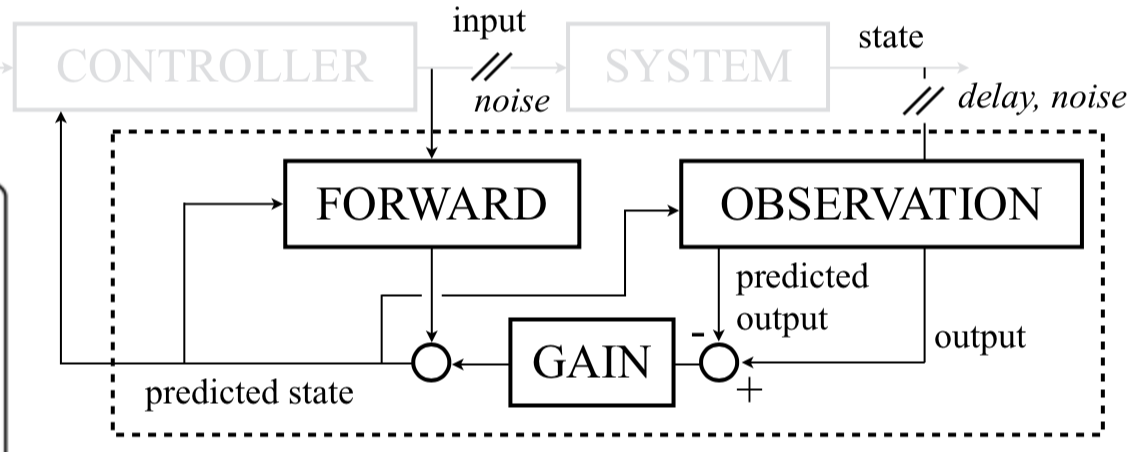
Two main theories of motor control
Task-dynamics approach: you assume that the whole system is a dynamical one, often with attractors ⟶ you can compute the spatio-temporal trajectory (movements result from convergence toward attractors)
⇒ you have no control on time, it comes from the dynamics.
Internal model approach: build control policy → inverse model of the system to follow a desired trajectory (optimization)
Optimality Principle
Adaptation of the behavior to the environment in an optimal way (e.g. spend as little energy as possible): to solve the redundancy problem
- Extension of the internal model approach:
-
control theory ⟶ optimal control theory
Objective function: minimization of task and action related quantities (cost, utility, energy, etc…)
Ex: mass at the end of a spring: find the smallest force $u(t)$ such that $x(t_0) = x_0, x(t_f) = x_f$ and:
\[m \ddot{x} + b \dot{x} + k(x-x_f) = u\]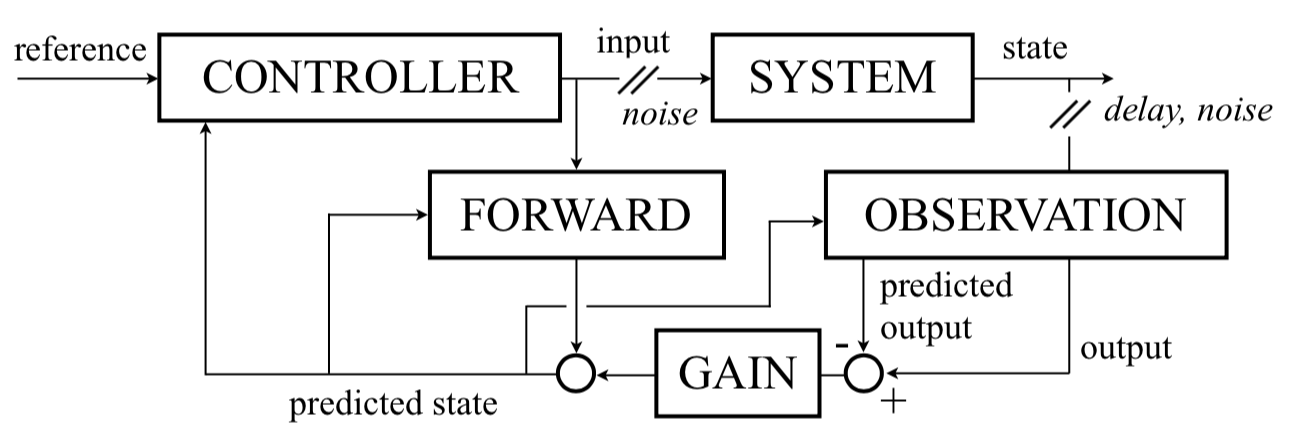
From movement to action
Movement
Ex: a monkey going from the position $\textbf{x}_0(t=t_0)$ to $\textbf{x}_f(t=t_f)$
Minimization:
\[J^\ast = \min_u \int_{t_0}^{t_f} \Vert \textbf{u}(t) \Vert^2 dt\]Reinforcement learning
Gives value to the states:
\[V(\textbf{x}_t) = 𝔼\left(\sum\limits_{ τ≥0 } γ^τ r_{t+τ} \mid \textbf{x}_t\right)\]Reward/effort trade-off
Combination of benefit and cost ($δ$: Dirac mass):
\[J^\ast = \max_{\textbf{u}} \int_0^∞ \exp(-t/γ) \overbrace{[\underbrace{ρ \, r \, δ(\Vert \textbf{x}^\ast - \textbf{x}(t) \Vert)}_{\text{benefit}} - \underbrace{ε \Vert \textbf{u}(t)}_{\text{cost}} \Vert^2]}^{\text{utility}} dt\]⟶ Time-flexibility
Extension: Decision theory
Bayesian inference
Neuroanatomy
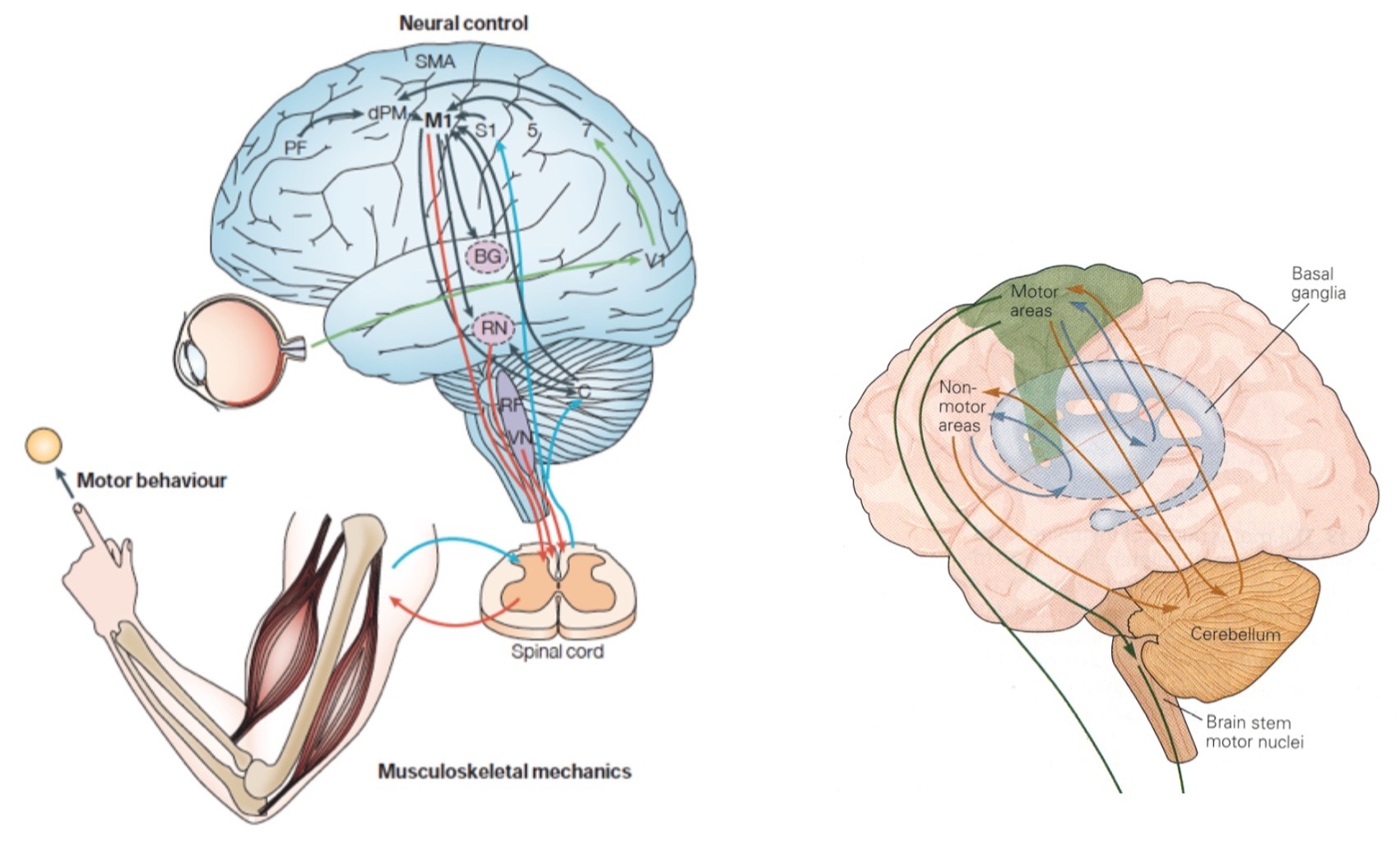
Anatomy: 4 important regions in the brain:
- Motor control area in the cortex (motor cortex)
- Spinal cord
- Basal ganglia
- Cerebellum
Computational architecture:
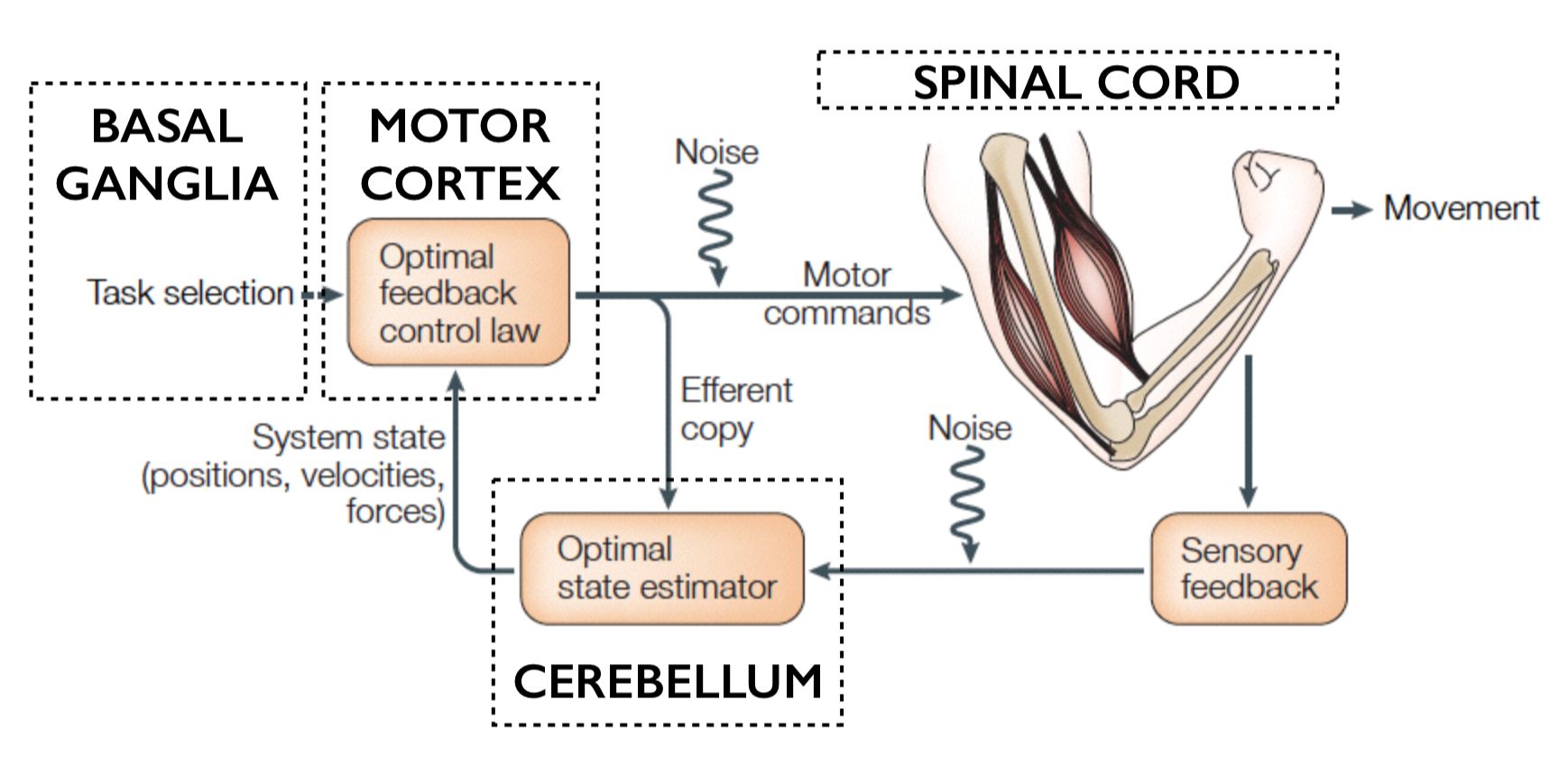
Leave a comment