DM1 : Théorème de Dilworth, Nombres de Catalan, Partitions entrelacées
Maths Discrètes : DM1
http://younesse.net/Maths-discretes/DM1/
Younesse Kaddar
EX 1
1.
Soit $F ⊆ E$ non vide.
- $\max(F)$ est une antichaîne
- car sinon, s’il y existait deux éléments distincts et comparables, le plus petit des deux ne serait pas un élément maximal.
- $\max(F)$ est non vide
- car sinon : pour tout $x_0 ∈ F$, il existe $x_1 ∈ F$ tel que :
- $x_0 ≤ x_1$
- $x_1 ≠ x_0$ Par un récurrence immédiate, on construit donc une suite strictement croissante (et donc injective) d’éléments à valeurs dans l’ensemble fini $F$ : absurde.
- car sinon : pour tout $x_0 ∈ F$, il existe $x_1 ∈ F$ tel que :
Donc $\max(F)$ est une antichaîne non vide de $E$.
2.
Pour $k=1$ : $E$ est une chaîne
- car sinon : il existerait deux éléments $x∈E$ et $y∈E$ non comparables, et la paire $\lbrace x,y\rbrace$ (de cardinal 2) contredirait la maximalité de $k$.
3.
a)
$E = F∪{z}$, où $z$ est un élément maximal, donc
\[\begin{align*} l+1 &= \max(\{|G|\}_{G ⊆ F, G \text{ antichaîne}}) + 1 \\ &≥ \max(\{|G|\}_{G ⊆ F∪\{z\}, G \text{ antichaîne}}) \\ & \hspace{1em}\text{ (les antichaînes de $F∪\{z\}$ ont au plus 1 élément de plus que celles de $F$) }\\ &= k \\ &≥ \max(\{|G|\}_{G ⊆ F, G \text{ antichaîne}}) \hspace{2em} \text{ (car $F⊆F∪\{z\}$)}\\ &= l \end{align*}\]Donc
\[l ≤ k ≤ l+1\]
b)
Comme toute partie d’une chaînes (resp. d’une antichaîne) reste une chaîne (resp. une antichaîne), ${\cal C}∩C_i$ est une chaîne et une antichaîne à la fois : elle ne contient qu’un élément ou aucun.
Donc \(\vert{\cal C}∩C_i\vert = 0 ∨ \vert{\cal C}∩C_i\vert = 1\)
c)
i)
Il existe une antichaîne ${\cal C}$ de \(E = \bigsqcup\limits_{1≤j≤l} C_j\) de cardinal $l$, et ${\cal C}$ intersecte chacun des $C_j$ en au plus un élément (par la question précédente) : donc
\[\vert C_i ∩ {\cal C} \vert = 1\](car sinon $\vert{\cal C}\vert < l$ )
et
$D_i$ est non vide.
ii)
Par l’absurde : s’il existait un $1≤i≠j≤l$ tel que
\(y_i ≼ y_j\) : alors comme il existe un élément $x_i∈C_i$ dans l’antichaîne de cardinal $l$ à laquelle appartient $y_j$ (cf. question précédente), et comme $x_i ≼ y_i ≼ y_j$ (par définition de $y_i$) : il vient que $x_i$ et $y_j$ sont comparables (par transitivité), ce qui est absurde.
iii)
Si $z$ n’est comparable avec aucun $y_i$ : alors
- $k=l+1$
- en effet : $l+1≥k$ et l’antichaîne $\lbrace y_1, ⋯, y_l, z \rbrace$ est de cardinal $l+1$.
- et \(E = \bigsqcup\limits_{1≤i≤l} C_i \sqcup \{z\}\) est une décomposition de $E$ en union de $l+1$ chaînes disjointes
iv)
Comme
- $z$ est comparable avec $y_i$
- $z$ est un élément maximal de $E$,
alors $y_i ≼ z$, et \(C' ≝ \{z\} ∪ \{x∈C_i | x≼y_i\}\)
est bien une chaîne (par transitivité).
- Cas 1 : Si $C_i\backslash C’=∅$ : alors il ne peut exister d’antichaîne de cardinal $l$ dans \(F\backslash C' = \Big(\bigsqcup\limits_{j ∈ ⟦1, l⟧\backslash \{i\}} C_j\Big) \sqcup (C_i\backslash C') \\ = \Big(\bigsqcup\limits_{j ∈ ⟦1, l⟧\backslash \{i\}} C_j\Big)\) puisque toute antichaîne intersecte chacun des $C_j$ (pour $j∈⟦1,l⟧\backslash\lbrace i\rbrace$) en au plus 1 élément (comme vu précédemment).
-
Cas 2 : sinon
Par l’absurde : s’il existait une antichaîne de cardinal $l$ dans
\[F\backslash C' = \Big(\bigsqcup\limits_{j ∈ ⟦1, l⟧\backslash \{i\}} C_j\Big) \sqcup (C_i\backslash C')\]alors elle intersecterait $C_i\backslash C’$ en au moins un élément $x_i∈C_i\backslash C’$, ce qui contredirait la maximalité de $y_i$.
- en effet : $x_i$ et $y_i$ seraient alors comparables, et $x_i ∈ C_i\backslash C’ ⟺ x_i \not≼ y_i ⟺ (y_i ≼ x_i ∧ x_i ≠ y_i)$
Il vient alors que :
- $k=l$
- car le cardinal d’une antichaîne de $F\backslash C’$ est majoré par $l-1$, donc, comme $C’$ est une chaîne : le cardinal d’une antichaîne de $E = (F\backslash C’) ∪ C’$ est majoré par $l$, et $\lbrace y_1, ⋯, y_l \rbrace$ en est une.
- Comme $l-1$ est le cardinal maximal d’une antichaîne de $F\backslash C’$ (puisque $\lbrace y_1, ⋯, y_l \rbrace \backslash \lbrace y_i \rbrace$ en est une) : par hypothèse de récurrence (forte) appliquée à $F\backslash C’$ : $F\backslash C’$ s’écrit comme une union de $l-1$ chaînes chaînes disjointes. Donc $E = F\backslash C’ \sqcup C’$ s’écrit comme union de $l$ chaînes disjointes.
4.
a).
On vérifie aisément que cette relation est réflexive, transitive, et antisymétrique : c’est donc une relation d’ordre.
Elle n’est pas totale car si $x_1 > x_2$ (pour l’ordre classique de ℕ), alors $x_1$ et $x_2$ sont incomparables.
-
Les chaînes sont les images de suites (indexées par un sous-ensemble de $⟦1,N⟧$) croissantes pour l’ordre de ${\cal F}$, i.e les ensembles de la forme $\lbrace n_{i_1}, ⋯, n_{i_j} \rbrace$, où :
\[n_{i_1} ≼ n_{i_2} ⋯ ≼ n_{i_j}\] -
Les antichaînes sont les images de suites (indexées par un sous-ensemble de $⟦1,N⟧$) strictement décroissantes pour l’ordre de $ℕ$, i.e les ensembles de la forme $\lbrace n_{i_1}, ⋯, n_{i_j} \rbrace$, où :
\[\begin{cases} i_1 < i_2 < ⋯ < i_j \\ n_{i_1} > n_{i_2} ⋯ > n_{i_j} \end{cases}\]
b).
Deux choses l’une :
-
Cas 1 : Soit ${\cal F}$ contient une antichaîne de cardinal supérieur (au sens large) à $m+1$.
Alors elle est l’image d’une d’une suite (indexée par un sous-ensemble de $⟦1,N⟧$) strictement décroissante pour l’ordre de $ℕ$ (cf. question précédente).
-
Cas 1 : Sinon : en notant $k ≤ m$ le maximum des cardinaux des antichaînes dans $({\cal F}, ≼)$, par le théorème démontré précédemment : ${\cal F}$ est la réunion de $k≤m$ chaînes $C_1, ⋯, C_k$ disjointes.
Enfin, il existe un indice $i∈⟦1,k⟧$ tel que \(\vert C_i \vert ≥ \left\lceil \frac{nm + 1}{m} \right\rceil = n+1\)
-
en effet : car sinon :
\[∀j∈⟦1,k⟧, \vert C_j \vert < \left\lceil \frac{nm + 1}{m} \right\rceil\]et
\[\begin{align*} N = \vert {\cal F} \vert &= \Bigg\vert \bigsqcup\limits_{j=1}^k C_j \Bigg\vert \\ &≤ \sum\limits_{j=1}^k \left( \left\lceil n + \frac{1}{m} \right\rceil - 1 \right) \\ &= k \left\lceil n + \frac{1}{m} \right\rceil - k \\ &= k \left( n + \left\lceil \frac{1}{m} \right\rceil \right) - k \\ &= k (n + 1) - k \\ &≤ mn = N-1 \end{align*}\]
On conclut en remarquant que $C_i$ est image d’une suite croissante (indexée par un sous-ensemble de $⟦1,N⟧$).
-
Dans tous les cas :
${\cal F}$ contient une suite croissante de cardinal $n+1$ ou une suite décroissante (pour l’ordre de $ℕ$) de cardinal $m+1$.
c).
Par l’absurde : Si ${\cal F}$ ne contenait ni suite croissante de cardinal $n+1$, ni suite décroissante (pour l’ordre de $ℕ$) de cardinal $m+1$.
En notant, pour tout $i∈⟦1,N⟧$, $c_i$ (resp. $d_i$) le cardinal de la plus grande sous-famille croissante (resp. décroissante, pour l’ordre de $ℕ$) qui débute en $n_i$, il vient alors que :
$∀ i ∈ ⟦1,n^2+1⟧$,
\[\begin{cases} 1 \leq c_i \leq n \\ 1 \leq d_i \leq m \end{cases}\]Or : $N=nm+1 > \vert ⟦1,n⟧\times ⟦1,m⟧ \vert$.
Donc, par le principe des tiroirs : il existe $i \neq j ∈ ⟦1,N⟧$ tels que :
\[(c_i, d_i) = (c_j, d_j)\]-
Cas 1 : Si $n_i \leq n_j$ :
En notant
\[(n_j, n'_2, ⋯, n'_{c_j})\]une suite croissante de cardinal $c_j$ débutant en $n_j$, la suite
\[(n_i, n_j, n'_2, ⋯, n'_{c_j})\]est croissante, de cardinal $c_j +1 = c_i + 1$, et débute en $n_i$, ce qui contredit la maximalité de $c_i$.
-
Cas 2 : Si $n_i > n_j$ :
En notant
\[(n_j, n'_2, ⋯, n'_{d_j})\]une suite décroissante de cardinal $d_j$ débutant en $n_j$, la suite
\[(n_i, n_j, n'_2, ⋯, n'_{d_j})\]est décroissante, de cardinal $d_j +1 = d_i + 1$, et débute en $n_i$, ce qui contredit la maximalité de $d_i$.
Dans tous les cas, on obtient une contradiction, donc
${\cal F}$ contient une suite croissante de cardinal $n+1$ ou une suite décroissante (pour l’ordre de $ℕ$) de cardinal $m+1$.
5.
On procède de manière analogue à 4.b), en munissant ${\cal I}$ de la relation binaire antisymétrique et réflexive :
\[[x_i, y_i] ≼ [x_j, y_j] ⟺ y_i < x_j\]NB :
\[C' = \{z\}∪\{x ∈ C_i \vert x ≤ y_i\}∪\{y_i\}\]
- Avec la convention que : pour tout intervalle $I$, $∅ ≼ I$
- On remarque que le théorème démontré en 2. et 3. n’utilise pas la réflexivité de la relation d’ordre, à condition de poser, en 3.c)iv) :
On peut donc l’appliquer avec cette relation binaire transitive et antisymétrique $≼$.
Pour cette relation :
- les chaînes sont les ensembles d’intervalles disjoints deux à deux.
-
deux intervalles sont incomparables si, et seulement si ils s’“enchevêtrent” ($(x_j ≤ y_i) ∧ (x_i ≤ y_j)$), i.e : ils sont non disjoints.
Les antichaînes sont donc les ensembles d’intervalles non disjoints deux à deux, c’est-à-dire les ensembles d’intervalles d’intersection non vide.
Deux choses l’une :
-
Cas 1 : Soit ${\cal I}$ contient une antichaîne de cardinal supérieur (au sens large) à $n+1$.
Alors le résultat est acquis.
-
Cas 1 : Sinon : en notant $k ≤ n$ le maximum des cardinaux des antichaînes dans $({\cal I}, ≼)$, par le théorème démontré précédemment : ${\cal I}$ est la réunion de $k≤n$ chaînes $C_1, ⋯, C_k$ disjointes.
De même qu’en 4.b), il existe un indice $i∈⟦1,k⟧$ tel que \(\vert C_i \vert ≥ \left\lceil \frac{nm + 1}{n} \right\rceil = m+1\)
Ce qui prouve l’existence de $m+1$ intervalles disjoints deux à deux.
Dans tous les cas :
Il existe $m+ 1$ intervalles dans ${\cal I}$ disjoints deux à deux ou $n + 1$ intervalles dans ${\cal I}$ d’intersection non vide.
EX 2
1.
a).
Soit $(p, q) ∈ ℕ^\ast\times ℕ^\ast$.
\[\begin{align*} \{ \text{chemins allant de $(0,0)$ à $(p,q)$}\} \\ &\hspace{-7em}=\{ \text{chemins allant de $(0,0)$ à $(p-1,q)$, suivis d'un pas à droite} \} \\ &\hspace{-6.8em}\sqcup \{ \text{chemins allant de $(0,0)$ à $(p,q-1)$, suivis d'un pas en haut} \} \\ \end{align*}\]Donc
\[\begin{align*} N_{p,q} &= \big\vert \{ \text{chemins allant de $(0,0)$ à $(p-1,q)$, suivis d'un pas à droite} \} \big\vert \\ &+ \big\vert \{ \text{chemins allant de $(0,0)$ à $(p,q-1)$, suivis d'un pas en haut} \} \big\vert \\ &= \big\vert \{ \text{chemins allant de $(0,0)$ à $(p-1,q)$} \} \big\vert \\ &+ \big\vert \{ \text{chemins allant de $(0,0)$ à $(p,q-1)$} \} \big\vert \\ &= N_{p−1,q} + N_{p,q−1} \end{align*}\]$∀p, q ≥1, N_{p,q} = N_{p−1,q} + N_{p,q−1}$
Donc en posant $∀p, q ∈ℕ, u_{p,p+q} = N_{p,q}$
- $∀q∈ℕ, u_{0, q} = 1$
- $∀p∈ℕ, u_{p, p} = 1$
- la suite $u$ vérifie la formule de Pascal
Donc $∀p ≤ q ∈ℕ, u_{p,q} = \binom{q}{p}$, et :
\[∀p, q ∈ℕ, N_{p,q} = \binom{p+q}{p}\]
b).
Pour tous $k,n ∈ℕ^\ast$ tels que $k≤n$ : $\binom{n}{k} = N_{k, n-k}$ est le nombre de chemins allant de $(0,0)$ à $(k, n-k)$
- en effet : la donnée d’un de ces chemins correspond à la donnée des $k$ pas à droite (les $n-k$ autres étant les pas vers le haut) parmi les $n$ pas d’une suite de $\lbrace pas_droite, pas_haut\rbrace^{⟦1,n⟧}$)
Donc en utilisant la relation (obtenue par des arguments combinatoires) : \(∀p, q ≥1, N_{p,q} = N_{p−1,q} + N_{p,q−1}\) la démonstration du triangle de Pascal s’ensuit.
c).
i).
Les valeurs prises par $𝛥$ sont contenues dans $⟦0,n⟧$ :
$𝛥$ est évidemment à valeurs positives, et le nombre de pas vers le haut, pour tout chemin $c$ de $(0,0)$ vers $(n,n)$ (n’utilisant que des des pas à droite et vers le haut) est borné par $n$.
- en effet: tout chemin contenant strictement plus de $n$ pas vers le haut est condamné à avoir une ordonnée finale strictement supérieure à $n$ (d’un pas à l’autre, l’ordonnée ne fait que croître).
$𝛥$ prend les valeurs $0, 1, ⋯, n$ :
On utilise les notations introduites en 1. c) iii).
Pour tout $i∈⟦0,n⟧$, en notant $c_i$ le chemin
\[\underbrace{\uparrow ⋯ \uparrow}_{i \text{ fois}} \, \underbrace{→ ⋯ →}_{n \text{ fois}} \, \underbrace{\uparrow ⋯ \uparrow}_{n-i \text{ fois}}\]on voit aisément que $𝛥(c_i) = i$
ii).
Les chemins $c$ tels que $𝛥(c)=0$ sont les chemins tels qu’aucun pas vers le haut n’est fait au-dessus de la diagonale, soit
les chemins restant toujours sous (au sens large) la diagonale.
Les chemins $c$ tels que $𝛥(c)=n$ sont les chemins tels que chacun des $n$ pas vers le haut est fait au-dessus de la diagonale, soit
les chemins restant toujours au-dessus (au sens large) la diagonale.
De plus : l’application qui à un chemin sous la diagonale associe son symétrique par rapport la diagonale est une bijection entre les ensembles $\lbrace c, 𝛥(c)=0 \rbrace$ et $\lbrace c, 𝛥(c)=n \rbrace$, donc :
$\vert \lbrace c, 𝛥(c)=0 \rbrace \vert = \vert \lbrace c, 𝛥(c)=n \rbrace \vert$
iii).
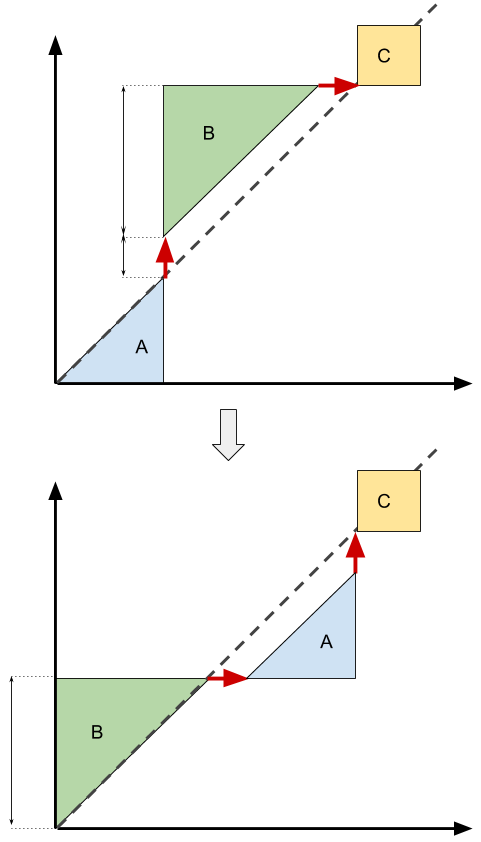
Notations et remarques préliminaires :
-
Pour tout $i∈⟦0,n⟧$, on pose
\[D_i ≝ \{ c, 𝛥(c) = i \}\] -
Pour tout chemin $c’$, on note :
- $nb_{haut}(c’)$ le nombre de pas vers le haut de $c’$
- $nb_{droite}(c’)$ le nombre de pas à droite de $c’$
- Les positions relatives (sous / au-dessus) sont toujours entendues au sens large.
- On pose $𝜑 ≝ c\mapsto \widetilde{c}$
Soit $i∈⟦1,n-1⟧$.
Montrons que $𝜑_{\vert D_i}$ est à valeurs dans $D_{i-1}$ :
Avec les notations de l’énoncé : soit
\[c=A\uparrow B→C \overset{\text{noté}}{=} A\uparrow_c B→_c C ∈ D_i\]Alors
\[\widetilde{c} ≝ B→A\uparrow C \overset{\text{noté}}{=} B→_\widetilde{c} A\uparrow_\widetilde{c} C\]Par définition des pas $\uparrow$ et $→$ explicités dans la factorisation précédente de $c$ (qu’on a notés respectivement $\uparrow_c$ et $→_c$):
\[𝛥(c) = 𝛥(A\uparrow_c B→_c) + 𝛥(C) \\ = 1 + 𝛥(B) + 𝛥(C)\]De plus, comme $\uparrow_c$ est le premier pas vers le haut au-dessus de la diagonale, et $→_c$ est le premier pas suivant rejoignant la diagonale, il vient que
$B$ reste au-dessus de la droite d’équation $y=x+1$ dans $c$ $(⊛)$
Donc, par translation de $-nb_{droite}(A)$ selon les abscisses, $-(nb_{haut}(A)+1)$ selon les ordonnées :
$B$ reste au-dessus la diagonale dans $\widetilde{c}$ $(⊛⊛)$
et
$→_\widetilde{c}$ est le premier pas rejoignant la droite d’équation $y=x-1$. $(\star)$
Comme $A$ restait sous la diagonale dans $c$,
$A$ reste sous la droite $y=x-1$ dans $\widetilde{c}$ $(⊛⊛⊛)$
et
$\uparrow_\widetilde{c}$ est le premier pas rejoignant ultérieurement la diagonale. $(\star \star)$
Enfin, comme les chemins $A\uparrow B→$ et $B→A\uparrow$ ont des $nb_{haut}$ et $nb_{droite}$ identiques,
le chemin $C$ est inchangé dans $c$ et $\widetilde{c}$. $(⊛⊛⊛⊛)$
D’après ce qui précède, dans le préfixe $A\uparrow_\widetilde{c} B→_\widetilde{c}$ de $\widetilde{c}$ : le préfixe $B$ est le seul chemin au-dessus de la diagonale.
Donc
\[𝛥(\widetilde{c}) = 𝛥(A\uparrow_\widetilde{c} B→_\widetilde{c}) + 𝛥(C) \\ = 𝛥(B) + 𝛥(C)\]et
\[\widetilde{c} ∈ D_{i-1}\]Montrons que $𝜑_{\vert D_i} : D_i ⟶ D_{i-1}$ est bijective :
On construit la bijection réciproque : $𝜓_{\vert D_{i-1}} : D_{i-1} ⟶ D_i$, en restreignant à $D_{i-1}$ l’application $𝜓$ définie de la manière suivante :
À tout chemin $c$ traversant non trivialement la diagonale se factorisant sous la forme :
\[B → A ↑ C\]où
- $→$ est le premier pas rejoignant la droite d’équation $y=x-1$
- $↑$ le premier pas suivant rejoignant la diagonale.
on associe le chemin $𝜓(c)$ décrit par le mot :
\[A ↑ B → C\]D’après les propriétés $(⊛), (⊛⊛), (⊛⊛⊛), (⊛⊛⊛⊛)$, et $(\star)$, $(\star \star)$ :
\[𝜑_{\vert D_i} \circ 𝜓_{\vert D_{i-1}} = id_{\vert D_{i-1}}\]Réciproquement :
Soit
\[c ≝ B→A\uparrow C \overset{\text{noté}}{=} B→A\uparrow C ∈ D_{i-1}\]Alors
\[𝜓(c)=A\uparrow B→C \overset{\text{noté}}{=} A\uparrow_{𝜓(c)} B→_{𝜓(c)} C\]Comme $→_c$ est le premier pas à droite sous la diagonale, et $\uparrow_c$ est le premier pas suivant rejoignant la diagonale, il vient que
$A$ reste sous la droite d’équation $y=x-1$ dans $c$.
Donc, par translation de $-(nb_{droite}(B)+1)$ selon les abscisses, $-nb_{haut}(B)$ selon les ordonnées :
$A$ reste sous la diagonale dans $𝜓(c)$
et
$\uparrow_{𝜓(c)}$ est le premier pas vers le haut au-dessus de la diagonale.
Comme $B$ restait au-dessus de la diagonale dans $c$,
$B$ reste au-dessus de la droite $y=x+1$ dans $𝜓(c)$
et
$→_{𝜓(c)}$ est le premier pas rejoignant ultérieurement la diagonale.
Enfin, comme les chemins $B→A\uparrow$ et $A\uparrow B→$ ont des $nb_{haut}$ et $nb_{droite}$ identiques,
le chemin $C$ est inchangé dans $c$ et $𝜓(c)$.
Donc
\[𝜓_{\vert D_{i-1}} \circ 𝜑_{\vert D_i} = id_{\vert D_i}\]et
$𝜑_{\vert D_i} : D_i ⟶ D_{i-1}$ est bien bijective.
En particulier :
\[∀i∈⟦1,n-1⟧, \vert D_i \vert = \vert D_{i-1} \vert\]iv)
\[c_n = \begin{cases} \vert \{ c , 𝛥(c) = 0 \} \vert = \vert \{ c , 𝛥(c) = n \} \vert \hspace{2em}\text{ (par 1.c)ii) ) } \\ \begin{align*} \vert \{ c , 𝛥(c) = 0 \} \vert &= \vert \{ c , 𝛥(c) = 2 \} \vert \\ &= \vert \{ c , 𝛥(c) = 3 \} \vert \\ &= ⋯ \\ &= \vert \{ c , 𝛥(c) = n-1 \} \\ &= \vert \{ c , 𝛥(c) = n \} \vert \hspace{2em}\text{ (par 1.c)iii) )} \end{align*} \end{cases}\]Donc, avec
\[\{\text{chemins allant de $(0,0)$ à $(n,n)$}\} = \bigsqcup\limits_{i=0}^n \{ c , 𝛥(c) = i \}\]il vient que :
\[\begin{align*} \binom{2n}{n} & = N_{n,n} \\ &= \vert\{\text{chemins allant de $(0,0)$ à $(n,n)$}\} \vert \\ &= \sum\limits_{i=0}^n \vert \{ c , 𝛥(c) = i \} \vert \\ &= \sum\limits_{i=0}^n c_n \\ &= (n+1)c_n \end{align*}\]Et enfin
\[c_n = \dfrac{\binom{2n}{n}}{n+1}\]
2.
a).
Toute partition de $⟦1,n⟧$ est une partie de l’ensemble des parties de $⟦1,n⟧$, donc
\[Part_n ≤ 2^{2^n}\]
b).
On vérifie qu’elle est :
- réflexive
- avec $𝜑 = id$
- antisymétrique
-
Si ${I_1, …, I_k} ≼ {J_1, …, J_l} ∧ {J_1, …, J_l} ≼ {I_1, …, I_k}$ et s’il existe des surjections $𝜑_1$ et $𝜑_2$ telles que
\[\begin{cases} ⟦1,k⟧ \overset{𝜑_1}{\twoheadrightarrow} ⟦1,l⟧ \\ ⟦1,l⟧ \overset{𝜑_2}{\twoheadrightarrow} ⟦1,k⟧ \\ \end{cases}\]alors
\[\begin{cases} k≥l \\ l≥k \\ \end{cases}\]d’où $l=k$ et les surjections sont des bijections, donc
\[∀t ∈ ⟦1,l⟧, J_t = \bigsqcup\limits_{s∈𝜑_1^{−1}(t)} I_s\]implique que les partitions sont égales.
-
- transitive
- en composant les applications surjectives fournies.
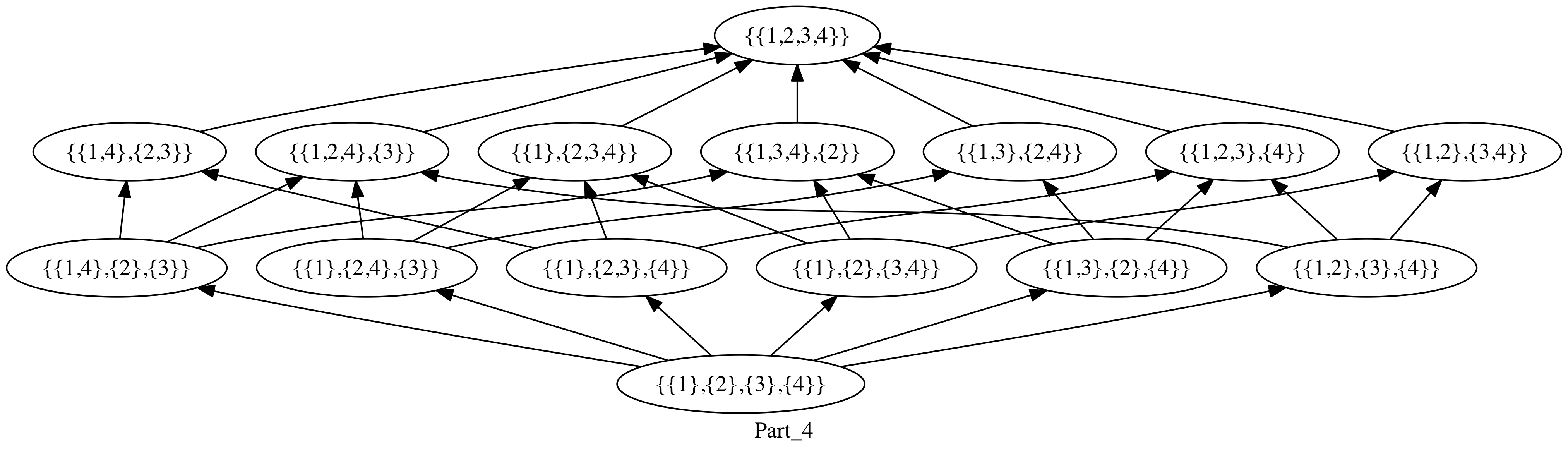
c).
d).
$Part_n$ est bien un treillis : pour toute paire de partitions $\lbrace 𝜋_1, 𝜋_2 \rbrace$
- on pose
\(\inf(𝜋_1, 𝜋_2) ≝ \{P_1 ∩ P_2\}_{(P_1, P_2) ∈ 𝜋_1 \times 𝜋_2, P_1 ∩ P_2≠∅}\)
- on vérifie que cette partition, plus fine que $𝜋_1$ et $𝜋_2$, est bien la borne inférieure de la paire :
- elle minore clairement $𝜋_1$ et $𝜋_2$
- pour toute partition $𝜋’$ plus fine que $𝜋_1$ et $𝜋_2$ : \(\begin{align*} &\hspace{1em}∀P'∈𝜋', ∃ (P_1, P_2) ∈ 𝜋_1 \times 𝜋_2; P'⊆P_1 ∧ P'⊆P_2 \\ ⟺&\hspace{1em} ∀P'∈𝜋', ∃ (P_1, P_2) ∈ 𝜋_1 \times 𝜋_2 \backslash\{(∅, ∅)\}; P'⊆P_1 ∧ P'⊆P_2 \\ ⟹&\hspace{1em} ∀P'∈𝜋', ∃ P_{inf} ∈ \inf(𝜋_1, 𝜋_2); P'⊆P_{inf} \\ ⟹&\hspace{1em} 𝜋' ≼ \inf(𝜋_1, 𝜋_2) \end{align*}\)
- on vérifie que cette partition, plus fine que $𝜋_1$ et $𝜋_2$, est bien la borne inférieure de la paire :
- on pose
- on vérifie que cette partition, moins fine que $𝜋_1$ et $𝜋_2$, est bien la borne supérieure de la paire :
- elle majore clairement $𝜋_1$ et $𝜋_2$
- pour toute partition $𝜋’$ moins fine que $𝜋_1$ et $𝜋_2$ : \(\begin{align*} &\hspace{1em}∀ P_1, ⋯ , P_k ∈ 𝜋_1 ∪ 𝜋_2, \hspace{0.8em} \bigwedge_{i=1}^{k-1} \Big( P_i ∩ P_{i+1}≠∅ \Big) ⟹ ∃P'∈𝜋'; \hspace{0.8em} \bigcup\limits_{i=1}^k P_i ⊆ P' \\ &\hspace{5em}\text{(des parties non disjointes sont incluses dans le même bloc)}\\ ⟹&\hspace{1em}∀ P_1, ⋯ , P_k ∈ 𝜋_1 ∪ 𝜋_2, \\ \hspace{0.8em}& \bigwedge_{i=1}^{k-1} \Big( P_i ∩ P_{i+1}≠∅ \Big) \\ &∧ \Bigg(∀P ∈ (𝜋_1 ∪ 𝜋_2) \backslash \{P_1, ⋯, P_k\}, P ∩ \bigcup\limits_{i=1}^k P_i = ∅\Bigg) ⟹ ∃P'∈𝜋'; \hspace{0.3em} \bigcup\limits_{i=1}^k P_i ⊆ P'\\ ⟹&\hspace{1em} ∀P_{sup} ∈ \sup(𝜋_1, 𝜋_2), ∃P'∈𝜋'; P_{sup} ⊆ P' \\ ⟹&\hspace{1em} \sup(𝜋_1, 𝜋_2) ≼ 𝜋' \end{align*}\)
3.
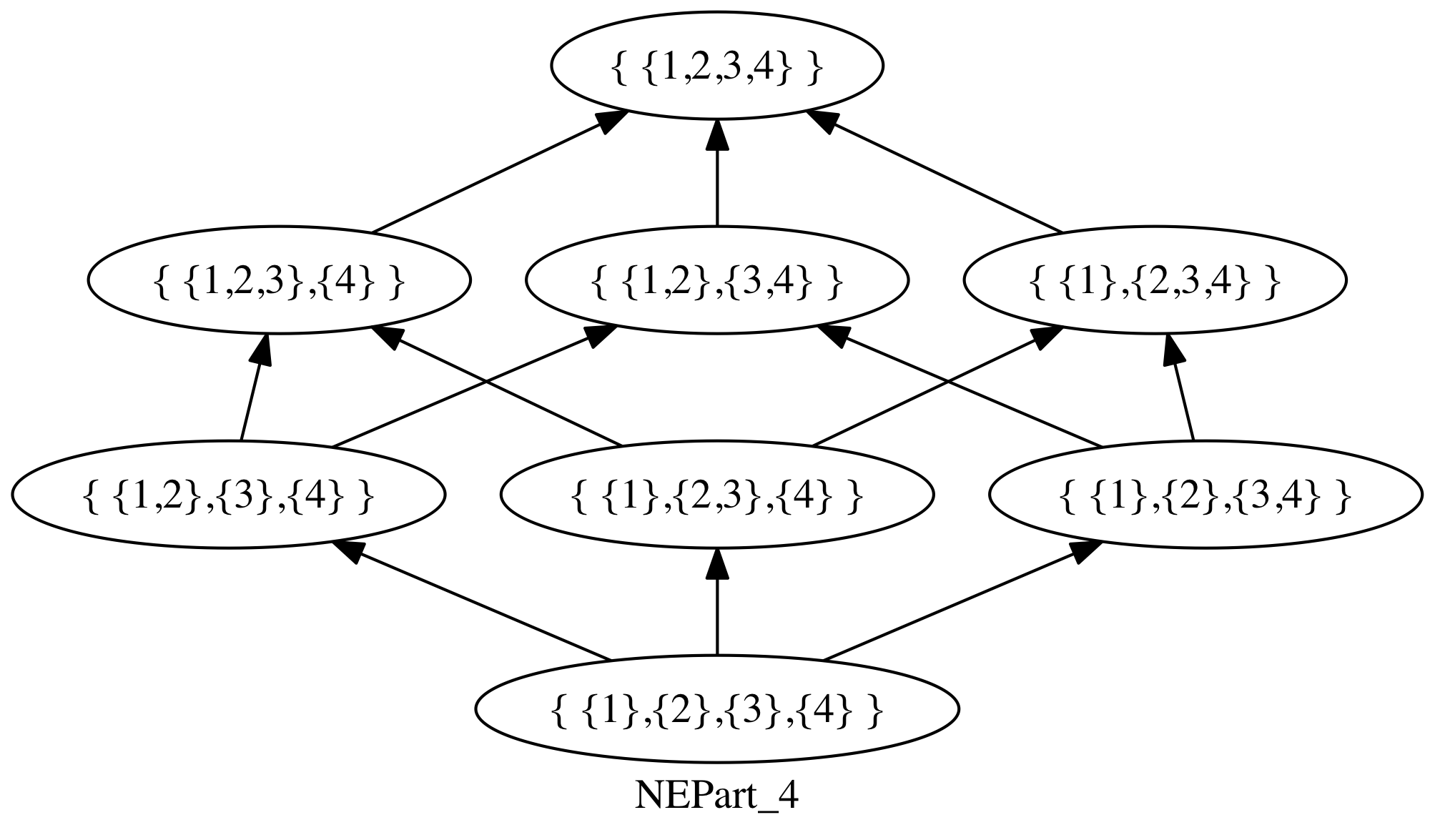
a).
b).
$NEPart_n$ est reste un treillis : pour toute paire de partitions $\lbrace 𝜋_1, 𝜋_2 \rbrace$, on vérifie aisément que les partitions $\inf(𝜋_1, 𝜋_2)$ et $\sup(𝜋_1, 𝜋_2)$ définies précédemment restent non entrelacées si tant est que $𝜋_1$ et $𝜋_2$ l’étaient.
c).
À toute partition $\lbrace I_1, ⋯, I_k \rbrace$ de $NEPart_n$ telle que :
\[∀s∈⟦1,k-1⟧, ∀t∈⟦s+1, k⟧, ∀i∈I_s, ∀j∈I_t, \hspace{0.8em} i<j\]on peut associer de manière biunivoque la partie de $⟦1,n-1⟧$ :
\[\{i ∈⟦1,n-1⟧ \, \vert \hspace{0.6em} ∃ s∈⟦1,k-1⟧, i = \max(I_s)\}\]Donc
\[\vert NEPart_n \vert = 2^{n-1}\]
Mais j’ai l’impression qu’en modifiant la définition de $NEPart_n$, on peut avoir
\[\vert NEPart_n \vert = c_n\]Il suffirait qu’on note $NEPart_n$ l’ensemble des partitions $\lbrace I_1, ⋯, I_k \rbrace$ de $⟦1,n⟧$ telles que :
\[∀s ≠ t ∈ ⟦1,k⟧, \\ ∀i ∈ I_s, (∀j ∈ I_t, i < j) ∨ (∀j ∈ I_t, i > j) \\ ∨ \Big( ∀i ∈ I_t, (∀j ∈ I_s, i < j) ∨ (∀j ∈ I_s, i > j) \Big)\]On aurait le diagramme de Hasse suivant pour $NEPart_4$ :
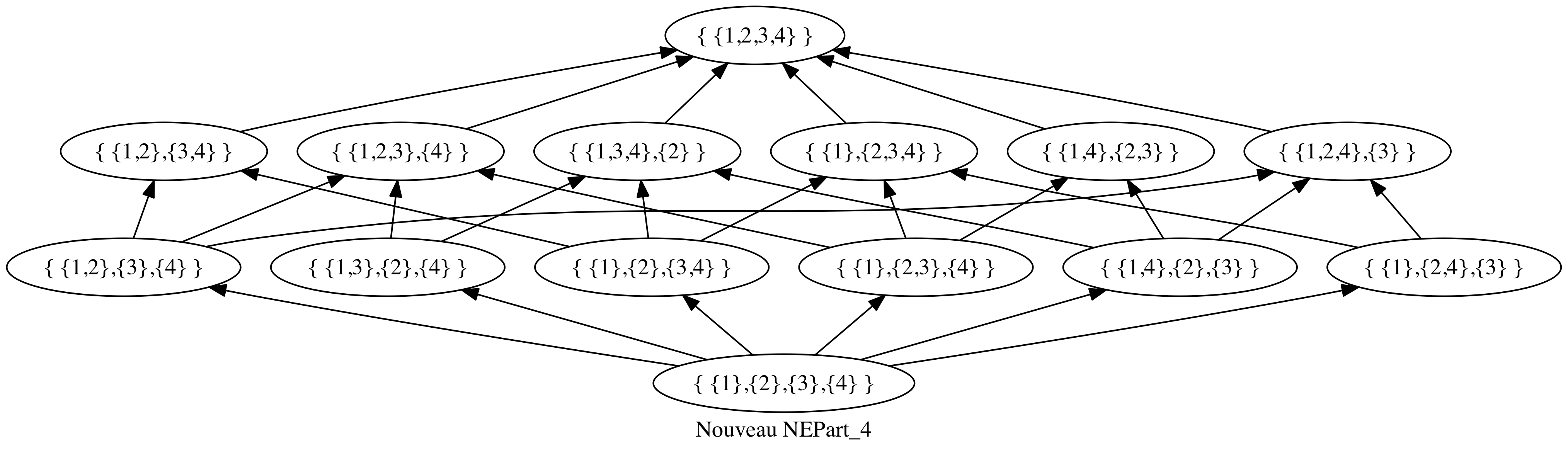
De plus, $\vert NEPart_n \vert$ vérifierait :
- $\vert NEPart_0 \vert = 1, \vert NEPart_1 \vert= 1, \vert NEPart_2 \vert = 2$
-
\[∀n∈ℕ, \vert NEPart_{n+1} \vert = \sum\limits_{i=1}^{n+1} \vert NEPart_{i-1} \vert × \vert NEPart_{n+1-i} \vert\]
- En effet : Pour toute partition $P$ de $⟦1,n+1⟧$, en notant $i$ le maximum du bloc contenant $1$ :
-
Comme $i$ et $1$ sont dans le même bloc : $P$ est la réunion
- d’une partition non entrelacée de $⟦i+1, n+1⟧$ (il y a $\vert NEPart_{n+1-i} \vert$ possibilités)
- et d’une partition non entrelacée de $⟦1,i-1⟧$, dont on a uni le bloc contenant $1$ au singleton $\lbrace i \rbrace$ (il y a $\vert NEPart_{i-1} \vert$ possibilités).
-
- En effet : Pour toute partition $P$ de $⟦1,n+1⟧$, en notant $i$ le maximum du bloc contenant $1$ :
Or, ces conditions initiales et cette relation de récurrence déterminent de manière unique la suite $(\vert NEPart_n \vert)_{n∈ℕ}$
Et :
-
Méthode 1 : en utilisant les séries formelles, comme on l’a fait en TD1, on peut montrer que :
\[\vert NEPart_n \vert = \dfrac{\binom{2n}{n}}{n+1} \overset{\text{donc}}{=} c_n\] -
Méthode 2 : On remarque que $c_n$, qui est le nombre de chemins allant de $(0,0)$ à $(n,n)$ en restant sous la diagonale, vérifie aussi ces conditions initiales et cette relation de récurrence :
-
en effet : tout chemin $c$ allant de $(0,0)$ à $(n+1, n+1)$ restant sous la diagonale se factorise de manière unique sous la forme : \(c = → c' \uparrow c''\)
où
- $\uparrow$ est le premier pas suivant rejoignant la diagonale
- il existe $i∈⟦0,n⟧$ tel que le sous-chemin $c’$ (resp. $c’’$) est un chemin allant de $(1,0)$ à $(i+1,i)$ (resp. de $(i+1,i+1)$ à $(n+1,n+1)$) en restant sous la droite d’équation $y=x-1$ (resp. la diagonale) : il y a $c_{i}$ (resp. $c_{n-i}$) tels sous-chemins.
-
Leave a comment