Cours 2 : Relations binaires/d’équivalence/d’ordre, Diagramme de Hasse, Treillis
Chapitre 2 : Relations
I. Relations binaires
- Relation binaire sur une ensemble $E$ :
-
la donnée d’une partie de $E\times E$
NB: Si $R⊆E\times E$, on note $xRy ⟺ (x,y)∈R$
Vocabulaire :
- Réflexive : $∀x, xRx$
- Symétrique : $∀ x,y ∈ E, xRy ⟹ yRx$
- Antisymétrique : $∀ x\neq y ∈ E, xRy ⟹ \lnot (yRx)$
- Transitive : $∀ x,y,z ∈ E, xRy ∧ yRz ⟹ xRz$
- Clôture transitive $R^{**}$ de $R$ :
- \[∀x, y ∈E, xR^{**}y ⟺ ∃n\geq 1, x_1, ⋯, x_n ∈ E ; \\ (x_0 = x) ∧ (x_i R x_{i+1} ∀i∈⟦0,n-1⟧) ∧ (x_n = y)\]
Proposition : $R^{**}$ est transitive.
Dém : Immédiate.
NB : Si $R$ est transitive, elle est égale à sa clôture transitive (dém : par récurrence sur la longueur du chemin de transitivité).
II. Relations d’équivalence
- Relation d’équivalence $R$ :
-
Relation binaire réflexive, symétrique et transitive.
- Classe d’équivalence de $x∈E$ pour $R$ :
-
$𝒞(x) ≝ {y∈E \vert xRy}$
Propriétés :
- $x ∈ 𝒞(x)$ (réflexivité)
- $∀ x, y ∈ E, xRy ⟺ 𝒞(x) = 𝒞(y)$ (une inclusion par transitivité PUIS égalité par symétrie)
- $∀ x, y ∈ E, xRy ⟺ 𝒞(x) ∩ 𝒞(y) \neq ∅$ (sens direct évident / transitivité pour le sens indirect)
Corollaire :
- L’ensemble des classes d’équivalence de la relation d’éq $R$ sur $E$ définit une partition de $E$.
- Réciproquement : toute partition de $E$ définit une relation d’éq dont les classes d’éq sont les éléments de la partition.
Dém :
- Immédiat, par les propriétés précédentes.
- $E = \bigsqcup_i E_i$ (chaque $E_i$ est non vide) ⟶ $xRy$ ssi $x, y$ sont éléments d’un même $E_i$ (alors unique).
- Ensemble quotient $E/R$ :
-
ensemble des classes d’éq de $R$ sur $E$.
- Surjection canonique :
- L’application \(𝜋 : \begin{cases} E ⟶ E/R \\ x \mapsto 𝒞(x) ≝ \{y ∈ E; xRy\} \end{cases}\)
est surjective : on l’appelle la surjection canonique (cf. théorie des catégories).
Proposition : Soit $f : E ⟶ F$ compatible avec $R$, i.e
\[∀x, y ∈ E, xRy ⟹ f(x)=f(y)\]Alors il existe $\bar{f} : E/R ⟶ F$ tq le diagramme suivant est commutatif : \({\displaystyle {\begin{matrix}E&\displaystyle {\xrightarrow {f}}&F\\\pi \downarrow &\displaystyle \nearrow \bar{f}\\E/R\end{matrix}}}\)
i.e $f$ se factorise à travers $E/R$ par la surjection canonique.
Dém : Si $xRy$, $f(x) = f(y)$.
Si $𝒞 ∈ E/R$, $f(x)$ est indépendant du choix de $x$ dans $𝒞$.
On pose $\bar{f}(𝒞) = f(x), x ∈ 𝒞$
NB:
- Catégories : définissent une structure avec les applications (morphismes) qui conservent cette structure : ici, le passage au quotient.
- Relation d’équivalence : regroupe des choses qui ont le même comportement.
III. Relations d’ordre
- Relation d’ordre $≤$ :
-
Relation binaire réflexive, antisymétrique, transitive.
NB:
- $<$ est la relation $≤ ∧ \neq$
- En maths, elles sont souvent totales, alors qu’en info : on utilise plus les relations partielles.
- Relation d’ordre $≤$ totale:
-
ssi $∀x, y ∈E, (x≤y) ∨ (y≤x)$
NB : Non total = partiel
Exs :
- $(ℕ, ≤), (ℝ, ≤)$ ordres totaux
- ordre lexicographique : $𝛴$ un ensemble ordonné.
Sur $𝛴^n$ (ensemble des mots de longueur $n$) : \(u = a_1 ⋯ a_n \\ v = b_1 ⋯ b_n\)
Si $u \neq v$, $∃ i; a_i \neq b_i$ (prenons $i$ minimal) :
- Si $a_i < b_i$ : $u<v$
- Si $a_i > b_i$ : $u>v$
NB: lexicographique ⟶ mots de même longueur VS alphabétique ⟶ mots pas forcément de même longueur
- Dans $ℕ^k$ : $(m_1, ⋯, m_k) ≤ (n_1, ⋯, n_k)$ si c’est le cas pour toutes les composantes.
⟶ l’ordre est partiel pour $k \geq 2$ (ex : $(0,1)$ et $(1,0)$ incomparables)
- L’inclusion dans $𝒫(E)$ est un ordre partiel.
- La divisibilité dans $ℕ^*$ : ordre partiel.
Vocabulaire
Pour classifier les relations d’ordre : quand deux relations d’ordre sont identiques, aux noms des éléments de l’ensembles près ?
- Chaîne :
-
Ensemble totalement ordonné.
- Antichaîne :
-
Ensemble muni d’une r.d’ordre (ro) \(x ≤ y ⟹ x = y\) (deux éléments distincts ne sont pas comparables).
- Successeur :
-
Soient $x, y ∈ E$ (muni de $≤$). $y$ est le successeur de $x$ ssi : \((y > x) ∧ ∀z∈E, y≥z≥x ⟹ y=z\) ($y$ est plus grand que $x$, et il n’y a rien entre les deux).
Proposition : Si $E$ est fini, $≤$ est la clôture transitive de la relation “successeur”.
Dém : Si $x, y ∈ E$ : \(x≤y ⟺ (x=y) ∨ ∃ x_0 = x, x_1, ⋯, x_n = y; x_i = succ(x_{i-1})\)
Diagramme de Hasse
La relation “successeur” peut être décrite par un diagramme de Hasse
Convention d’écriture : du bas vers le haut, et $x$ (en bas) relié à $y$ (en haut) ssi $x≤y$
Exs :
- Diagramme de Hasse d’un chaîne : points alignés verticalement
- Diagramme de Hasse d’un antichaîne : points alignés horizontalement.
NB: But du diagramme de Hasse : ignorer le nom des éléments de l’ensemble, et se focaliser sur la ro.
Ex :
Diviseurs de $30$ : (cf. diagramme)
- Application monotone :
-
$f : (E, ≤) ⟶ (F, ≤)$ est monotone (croissante) ssi \(∀x, y∈E, x≤y ⟹ f(x)≤f(y)\)
Pourquoi “seulement monotone”, et pas croissante ?
Parce que pour tout ordre, il y a l’ordre dual (ordre inverse) : selon qu’on considère l’ordre ou son dual, la fonction est croissante ou décroissante.
NB : fonctions monotones = morphismes de relations d’ordre
- Plus petit élément / minimum :
-
$(E, ≤)$ admet un plus petit élément, noté $\bot$ ssi : \(∀x∈E, \bot \leq x\)
- Plus grand élément / maximum :
-
$(E, ≤)$ admet un plus grand élément, noté $\top$ ssi : \(∀x∈E, \top \geq x\)
Ex :
- $ℕ$ admet un plus petit élément (0), mais pas de plus grand élément.
- $ℤ$ : ni de plus petit, ni de plus grand élément.
- Même un ensemble fini peut ne pas avoir de plus petit ou de plus grand élément (ex: antichaîne, ensemble non totalement ordonné, etc…)
- Élément maximal :
-
$x∈F$ est dit maximal dans $F$ ssi \(∀y∈F, y ≥ x ⟹ y=x\)
- Élément minimal :
-
$x∈F$ est dit minimal dans $F$ ssi \(∀y∈F, y ≤ x ⟹ y=x\)
NB:
- Il faut déjà que $y$ et $x$ soient comparables.
- Plus grand élément ⟹ Élément maximal, et c’est l’unique : on l’appelle le maximum de $F$.
- Plus petit élément ⟹ Élément minimal, et c’est l’unique : on l’appelle le minimum de $F$.
NB : Unique élément maximal $\not⟹$ Plus grand élément
Ex : $ℕ$, et un élément non comparable aux entiers (cet élément non comparable est un élément maximal, mais pas un maximum).
Prop : Soit $F$ fini. Si $F$ admet un unique élément maximal, alors c’est un maximum.
Dém : En notant $c$ cet élément, si $x \neq c$ : $x<z$ pour un certain $z$, et on conclut par réc sur $\vert F\vert $ en considérant $F\backslash{x}$.
- Majorant :
-
$F⊆E$ : $y∈E$ est un majorant de $F$ ssi \(∀x∈F, y ≥ x\)
- Minorant :
-
idem
- Borne supérieure :
-
Minimum de l’ensemble des majorants, s’il existe.
- Borne inférieure :
-
idem
Prop : Plus grand élément ⟹ Borne sup (idem pour petit/inf)
Dém : En posant $c ≝ max(F)$ : on vérifie aisément que c’est le plus petit (par définition des majorants, et comme $c∈F$) majorant (c’est un maximum).
NB : La réciproque est fausse (ex: $ℝ \supset ]0,1[$).
Prop : Borne supérieure appartenant à l’ensemble ⟹ maximum
Dém : c’est un majorant et il appartient à $F$.
Ex :
1) $(ℕ\backslash{0}, \vert )$
$F={a_1, ⋯, a_n}$ :
- les majorants de $F$ sont les multiples communs aux $a_i$, leur plus petit élément est $ppcm(a_1, ⋯, a_n)$.
- les minorants de $F$ sont les diviseurs communs aux $a_i$, leur plus petit élément est $pgcd(a_1, ⋯, a_n)$.
2) $(E, ≤) = (𝒫(X), ⊆)$, $F = {Y_1, ⋯, Y_n}$ : un majorant contient les $Y_i$,
- Borne sup : $\bigcup_i Y_i$
- Borne inf : $\bigcap_i Y_i$
Treillis
- Treillis :
-
Ensemble ordonné dans lequel toute paire (d’éléments) admet une borne sup et une borne inf. (cf. diagramme de Hasse qd $x,y$ non comparables).
- Treillis complet :
-
Si, de plus, pour toute partie $F ⊆ E$, $F$ admet un borne sup et une borne inf.
Supposer que l’existence d’une borne sup suffit : l’existence d’une borne inf est un théorème.
Dém :
Considérons le sup $a_0$ de l’ensemble $A$ des minorants d’une partie $B$.
Si $a_0 ∈ A$, $a_0$ est une borne inf de $B$.
Montrons que c’est le cas : pour tout $b∈B$, mq $a_0 ≤ b$, i.e $∀a∈A, a ≤ b$.
Si $a∈A$, $a ≤ b$ est bien, par définition de $A$ (ensemble des minorants de $B$).
NB : Un treillis complet a un plus grand (resp. petit) élément, puisque $E ⊆ E$ a une borne sup (qui lui appartient ⟶ plus grand élément).
Ex:
1) $(ℕ\backslash{0}, \vert )$ est un treillis (non complet, car seules les parties finies admettent une borne sup a priori (l’ensemble $ℙ$ n’a pas de majorant)).
2) $(𝒫(X), ⊆)$ est un treillis complet :
- Borne sup de $S⊆𝒫(X)$ = $\bigcup_{Y∈S} Y$
- Borne inf de $S⊆𝒫(X)$ = $\bigcap_{Y∈S} Y$
3) Pour une topologie, l’ensemble des ouverts est un treillis complet (l’union d’ouverts reste un ouvert (borne sup)).
L’inf d’une famille d’ouverts, c’est l’intérieur de l’intersection.
- Point fixe d’une applcation $f: E ⟶ E$ :
-
Un élément $x$ tq $f(x)=x$
Th de Knaster-Tarski : Soit $(E,≤)$ un treillis complet, $f: E ⟶ E$ monotone.
Alors $f$ admet un plus petit pt fixe, et un plus grand pt fixe.
NB :
- fonction “monotone” : c’est un anglicisme (pour dire “croissante”).
- en fait, on a même mieux : l’ensemble des points fixes est un treillis complet.
-
Heuristique :
- $(f^n(\bot))_n$ est une suite croissante.
- si en on note $f^𝜔(\bot)$ le sup : on a $f^𝜔(\bot) ≤f^{𝜔+1}(\bot)$
- puis, avec les ordinaux : $f^{𝜔^k}(\bot) ≤f^{𝜔^{k+1}}(\bot)$
- particularité des ordinaux : le sup d’une famille est un ordinal
- puis : paradoxe de Burali-Forti
- l’ensemble de tous les ordinaux est un ordinal : bizarre car cet ordinal est alors strictement plus grand que lui-même (à la Russel)
- en fait : il n’y a pas d’ensemble des ordinaux.
- donc ici : comme on a bien a affaire à un ensemble, on ne peut pas avoir stricte croissance de la suite précédente ⟶ il y a un point fixe.
Dém :
On pose $F≝ \lbrace x∈E; x\leq f(x)\rbrace$
NB : un $x$ tel que $x≤f(x)$ s’appelle un post-point fixe (même déf pour “pré-point fixe”)
On remarque que $\bot ∈ F$, donc $F \neq ∅$.
Comme $(E,≤)$ est un treillis complet, $F$ admet une borne sup $y$.
Mq $y∈F$ :
Soit $x∈F$ : $x≤y$, et donc ($f$ monotone) $f(x)≤f(y)$.
Ainsi \(x ≤ f(x) ≤ f(y)\)
Donc $f(y)$ majore $F$, et donc \(y ≤ f(y)\) ($y$ : + petit des majorants de $F$), donc $y ∈ F$ (déf de $F$).
Par monotonie de $f$ : $f(F)⊆F$.
Donc $f(y) ∈ F$, et donc $f(y) ≤ y$, d’où \(y = f(y)\)
Comme $F$ contient tous les pts fixes de $f$, alors $y$ est le plus grand point fixe de $f$.
(dém analogue pour la borne inf)
Application : Th de Cantor-Bernstein
Dém :
Soient $E, F$ deux ensembles, $f: E⟶F$ et $g: F⟶E$ injectives.
On pose \(H ≝ \begin{cases} 𝒫(E) ⟶ 𝒫(E) \\ X \mapsto E\backslash g(F\backslash f(X)) \end{cases}\)
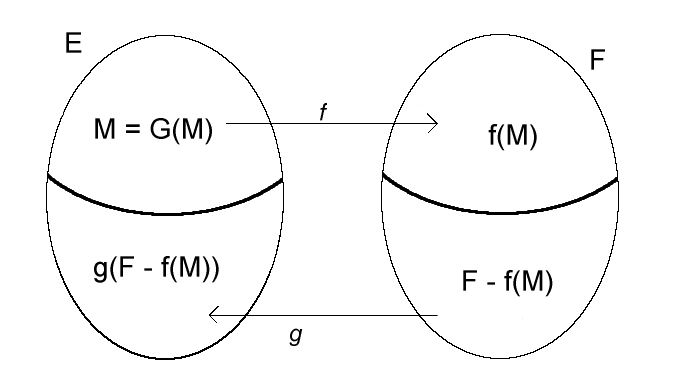
($H = G$ sur ce dessin)
1) Mq $H$ est monotone.
Soient $X, Y ⊆ E$ tq $X⊆Y$.
\[\begin{align*} X⊆Y &⟹ f(X) ⊆ f(Y) \\ &⟹ F\backslash f(Y) ⊆ F\backslash f(X) \\ &⟹ g(F\backslash f(Y)) ⊆ g(F\backslash f(X)) \\ &⟹ H(X) = E\backslash g(F\backslash f(X)) ⊆ H(Y) = E\backslash g(F\backslash f(Y)) \end{align*}\]Par le th de Knaster-Tarski, $H$ admet un point fixe $Z$.
\[Z = H(Z) = E\backslash g(F\backslash f(Z)) \\ ⟹ E\backslash Z = g(F\backslash f(Z))\]On définit \(h ≝ \begin{cases} E ⟶ F \\ x \mapsto \begin{cases} f(x) \text{ si } x∈Z \\ g^{-1}(x) \text{ sinon. } \end{cases} \end{cases}\)
NB : Comme $E\backslash Z = g(F\backslash f(Z))$, si $x \not ∈ Z$, $∃u ∈ F\backslash f(Z); x = g(u)$, et $u$ est unique par injectivité de $g$.
Mq $h$ est injective :
Si $x,y ∈E; h(x) = h(y)$.
- Si $x, y∈Z$ : $x=y$ par injectivité de $f$
- Si $x, y\not∈Z$ : $x,y$ ont le même antécédent par $g$, donc $x=y$
- Si $x∈Z, y\not∈Z$ : $h(x) = f(x) ∈ f(Z)$, $h(y) = g^{-1}(y) ∈ F\backslash f(Z)$, donc $h(x) \neq h(y)$.
Mq $h$ est surjective :
Soit $y ∈ F$.
- Si $y ∈ f(Z), ∃ z ∈ Z; y = f(z)$, et $y = f(z) = h(z)$
- Si $y \not∈ f(Z), y = g^{-1}(g(y)) = h(g(y))$
Langages algébriques
Langages reconnus par automates à piles.
Ex :
Grammaire :
- $S ⟶ 𝜀$
- $aSb$
⟹ Langage ${a^n b^n, n ∈ ℕ}$
$f({\cal L}) = {\cal L} ∪ a {\cal L} b$
${a^n b^n, n ∈ ℕ}$ est le plus petit point fixe de $f$.
- Directed Complete Partial Order (DCPO) :
-
Un ensemble partiellement ordonné tel que toutes les familles dirigées aient des bornes sup.
- Famille dirigée $(x_i)_{i∈I}$ d’élément de $X$ :
-
- famille non vide
- telle que : $∀i, j, ∃ k; x_i, x_j ≤ x_k$
graph mon_graphe {
rankdir=BT;
x_i -- x_k;
x_j -- x_k;
}
Exs de DCPO :
- tout treilis complet
-
L’ensemble de Scott
\[\{[a,b] \vert \, \, a, b ∈ ℝ, a≤b\}\]muni de l’ordre $\supseteq$
NB : ça n’est pas un treillis complet, à cause de l’ensemble vide.
- $f : X ⟶ Y$ est Scott-continue ssi :
-
- $f$ monotone
- $∀(x_i)_{i∈I}$ dirigée dans $X$, \(\sup_{i∈I} f(x_i) = f(\sup_{i∈I} x_i)\)
NB :
- ça coïncide bien avec la continuité pour la topologie de Scott.
- la famille $(f(x_i))_i$ est dirigée, d’où l’existence du sup
-
pour vérifier cette égalité, on procède par double inégalité, sachant que $\sup_{i∈I} f(x_i) ≤ f(\sup_{i∈I} x_i)$ est toujours vraie
- seule chose à démontrer, sachant que $f$ monotone : $\sup_{i∈I} f(x_i) ≥ f(\sup_{i∈I} x_i)$
Th de Kleene : Soit $X$ un dcpo pointé (i.e avec un plus petit élément $\bot$).
Toute fonction Scott-continue $f: X ⟶ X$ a un plus point fixe :
\[lfp(f) ≝ \sup_{n∈ℕ} f^n(\bot)\]
$(f^n(\bot))_n$ est une chaîne, donc dirigée.
Posons
\[x = \sup_n f^n(\bot)\]Alors :
\[f(x) = f(\sup_n f^n(\bot)) \\ = \sup_n f^{n+1}(\bot)\](par Scott-continuité)
Donc :
\(x = f(x)\) et $x$ est un point fixe.
Montrons que c’est le plus petit :
Si $y$ est un autre point fixe :
\[\bot ≤ y \\ ⟹ f(\bot) ≤ f(y)=y \\ ⟹ ∀n, f^n(\bot) ≤ y \\ ⟹ x ≤ y\]($x$ est le sup = le plus petit des majorants)
Axiome du choix
Existence d’une fonction de choix :
- Dans le cas fini : trivial
- Dans le cas dénombrable : accepté, sinon, pas de maths
- Dans le cas non dénombrable : controversé
Théorème de Bourbaki-Witt : Soit $(X, ≤)$ un ensemble ordonné tel que toute chaîne non vide admet une borne supérieure.
Soit $f : X ⟶ X$ une application telle que $∀x ∈ X, x ≤ f(x)$. Alors $f$ admet un point fixe.
Dém :
NB1 : Si $X$ est une chaîne, en notant $c$ sa borne supérieure. Alors \(c ≤ f(c) ≤ c\) donc le th est vrai.
NB2 : Si $a ∈ X$. \(X_a ≝ \{x∈X \vert x ≥ a\}\)
La borne sup d’une chaîne de $X_a$ reste donc dans $X_a$.
De plus, si $x ∈ X_a$, $f(x)≥x≥a$, donc $f(X_a)⊆X_a$.
On peut donc se ramener au cas où $X$ admet un plus petit élément $\bot$.
- Partie admissible :
-
Une partie qui vérifie :
- $\bot ∈ A$
- $f(A) ⊆ A$
- Si $C$ est une chaîne non vide de $A$, alors sa borne sup (dans $X$) reste dans $A$.
NB :
- $X$ est admissible
- Les parties admissibles sont stables par intersection.
On note $M$ l’intersection de l’ensemble des parties admissibles (c’est donc la plus petite).
- Élément extrême :
-
Un élément $c∈M$ tq \(∀x∈M, x<c ⟹ f(x)≤c\)
Si $c$ est extrême, on pose \(M_c ≝ \{x ∈ M \vert (x ≤ c) ∨ (f(c) ≤ x)\}\)
Mq $M_c$ est admissible.
-
$\bot ≤ c$ donc $\bot ∈ M_c$
- Soit $x∈M_c$.
- Si $x<c$, alors $f(x)≤c$ ($c$ extrême), donc $f(x)∈M_c$
- Si $x=c$, $c≤f(c)=f(x)$, donc $f(x)∈M_c$
- Si $x>c$, $f(c)≤x≤f(x)$ donc $f(x)∈M_c$
- $C$ une chaîne dans $M_c$ :
- Si $∀x∈C, x≤c$, alors $\sup_X(C) ≤ c$ (par déf de la borne sup)
- Sinon $∃x ∈ C, x>c$ alors $f(c)≤x≤\sup_X(C)$
Par minimalité de $M$, il vient que : \(c \text{ extrême} ⟹ M_c = M\)
Mq tous les éléments de $M$ sont extrêmes.
\[E≝\{c∈M; c \text{ extrême}\}\]On mq $E$ est admissible :
- $\bot$ est extrême car ${x; x<\bot } = ∅$
- Soit $c$ extrême :
Soit $x∈M$ tq $x<f(c)$ :
- Si $x<c, f(x)≤c≤f(c)$
- Si $x=c$, $f(x)=f(c)$
- Si $x>c$, $M_c=M$, donc $f(c)≤x≤f(x)$ : ce cas ne peut pas se produire car il contredit $x<f(c)$
- Soit $C$ une chaîne dans $E$, $s ≝ \sup_X(C)$
On veut mq $s$ est extrême. Soit $x ∈ M$ tq $x<s$.
- 1er Cas : $∃y ∈ C; x<y$, donc comme $y$ est extrême, on a \(f(x)≤y≤s\)
- 2e Cas : $∀ y ∈ C, \lnot (x<y)$ : $M_y = M$ donc pour tout $C∋y≠x$, $f(y)≤ x$, et $y≤f(y)≤x$ est vrai pour tout $y∈C$, d’où $s≤x$ : contradiction.
Donc $E=M$ (minimalité de $M$).
On en déduit que $M$ est une chaîne :
Soient $x,y ∈ M$.
\(M = M_y = \{z; z≤y ∨ f(y)≤z\}\) $x ∈M$, i.e $x≤y$, ou $f(y)≤x$, mais alors $y ≤ f(y) ≤x$.
Donc le résultat est acquis. ___
Lemme de Zorn : Soit $X$ un ensemble ordonné dans lequel toute chaîne admet une borne supérieure. Alors $X$ admet un élément maximal.
Corollaire :
- Tout corps admet une clôture algébrique.
- Dans tout anneau, il y a un idéal maximal.
Dém :
\(𝒳 ≝ \{\text{chaînes de $X$}\}\) ordonné par l’inclusion.
Soit
\[(𝒞_i)_{i∈I}\]une famille tot. ordonnée de chaînes : alors $\bigcup 𝒞_i$ est dans $𝒳$ et est donc la borne sup de $(𝒞_i)$.
Si $𝒳$ ne possède pas d’élément maximal, \(∀𝒞 ∈𝒳, ∃ 𝒞'∈𝒳; 𝒞 ⊊ 𝒞'\)
\(f : \begin{cases} 𝒳 ⟶ 𝒳 \\ 𝒞 \mapsto f(𝒞); 𝒞 ⊊ f(𝒞) \end{cases}\) (utilise l’axiome du choix) : contradiction avec Bourbaki-Witt.
Donc $𝒳$ possède un élément maximal $𝒞$.
Soit $s ≝ \sup_X(𝒞)$.
Alors $s$ est maximal dans $X$ : sinon, $∃ t ∈X; t>s$ et comme $𝒞 ⊊ 𝒞∪{t}$ : $𝒞$ n’est pas maximal.
Leave a comment