Exercise Sheet 6: integrate-and-Fire Neuron
Exercise Sheet 6: Integrate-and-Fire Neuron
Younesse Kaddar
\[\newcommand{\d}{ {\rm d}} \newcommand{\e}{ {\rm e}}\]PDF Version / Online Version
1. Integrate-and-Fire Neuron
We consider the integrate-and-fire neuron with differential equation:
\[τ \frac{\d V(t)}{\d t} = E_L - V(t) + RI(t)\]Whenever the voltage reaches a threshold, $V ≥ V_{\text{th}}$ is set back to the equilibrium potential $V = E_L$
a). Consider a constant current $I(t) = I_0$. How large must $I_0$ be so that the neuron starts spiking?
Let us solve the integrate-and-fire neuron’s differential equation in this case:
\[\begin{align*} \quad & τ \frac{\d V(t)}{\d t} = E_L - V(t) + RI_0\\ ⟺ \quad & \frac{ \d V(t)}{ \d t} = \frac{E_L + RI_0}{τ} - \frac{V(t)}{τ}\\ ⟺ \quad & \frac{ \d V(t)}{ \d t} + \frac 1 {τ} \, V(t) = \frac {E_L + RI_0} {τ}\\ ⟺ \quad & \frac{ \d V(t)}{ \d t} \, \e^{t/τ} + \frac 1 {τ} \, V(t) \, \e^{t/τ} = \frac {E_L + RI_0} {τ} \, \e^{t/τ}\\ ⟺ \quad & \frac{ \d}{ \d t} \left[V(t) \, \e^{t/τ}\right] = \frac {E_L + RI_0} {τ} \, \e^{t/τ}\\ ⟺ \quad & V(t) \, \e^{t/τ} =\frac {E_L + RI_0} {τ} \, τ \; \e^{t/τ} + \text{const}\\ ⟺ \quad & V(t) \, \e^{t/τ} = \left(E_L + R I_0 \right) \, \e^{t/τ} + \text{const}\\ ⟺ \quad & V(t) = \left(E_L + R I_0 \right) + \text{const} × \e^{-t/τ}\\ \end{align*}\]And with $V(0) = E_L$:
\[E_L = E_L + R I_0 + \text{const} \; ⟺ \; \text{const} = - R I_0\]Therefore:
\[V(t) \, = E_L + R I_0 \left(1-\e^{-t/τ}\right)\]
As a result:
\[\begin{align*} \quad & \; V(t) \, \overset{\text{eventually}}{≥} V_{th}\\ ⟺ \quad & \; \underbrace{\lim\limits_{t \to +∞} V(t)}_{= \; E_L + R I_0} ≥ V_{th} &&\text{(as } V \text{ is monotonous before spiking)}\\ ⟺ \quad & \; E_L + R I_0 ≥ V_{th}\\ ⟺ \quad & \; I_0 ≥ \frac{V_{th} - E_L}{R} \end{align*}\]Thus, for the neuron to start spiking, it is necessary that:
\[I_0 ≥ \frac{V_{th} - E_L}{R}\]
This is illustrated by the following plot, where we set
- $R ≝ 10 \text{ MΩ}$
- $E_L ≝ −70 \text{ mV}$ (reversal potential)
- $τ ≝ 10 \text{ ms}$
- $V_{th} ≝ -63 \text{ mV}$
as a result of which $\frac{V_{th} - E_L}{R} = 0.7 \text{ nA}$:
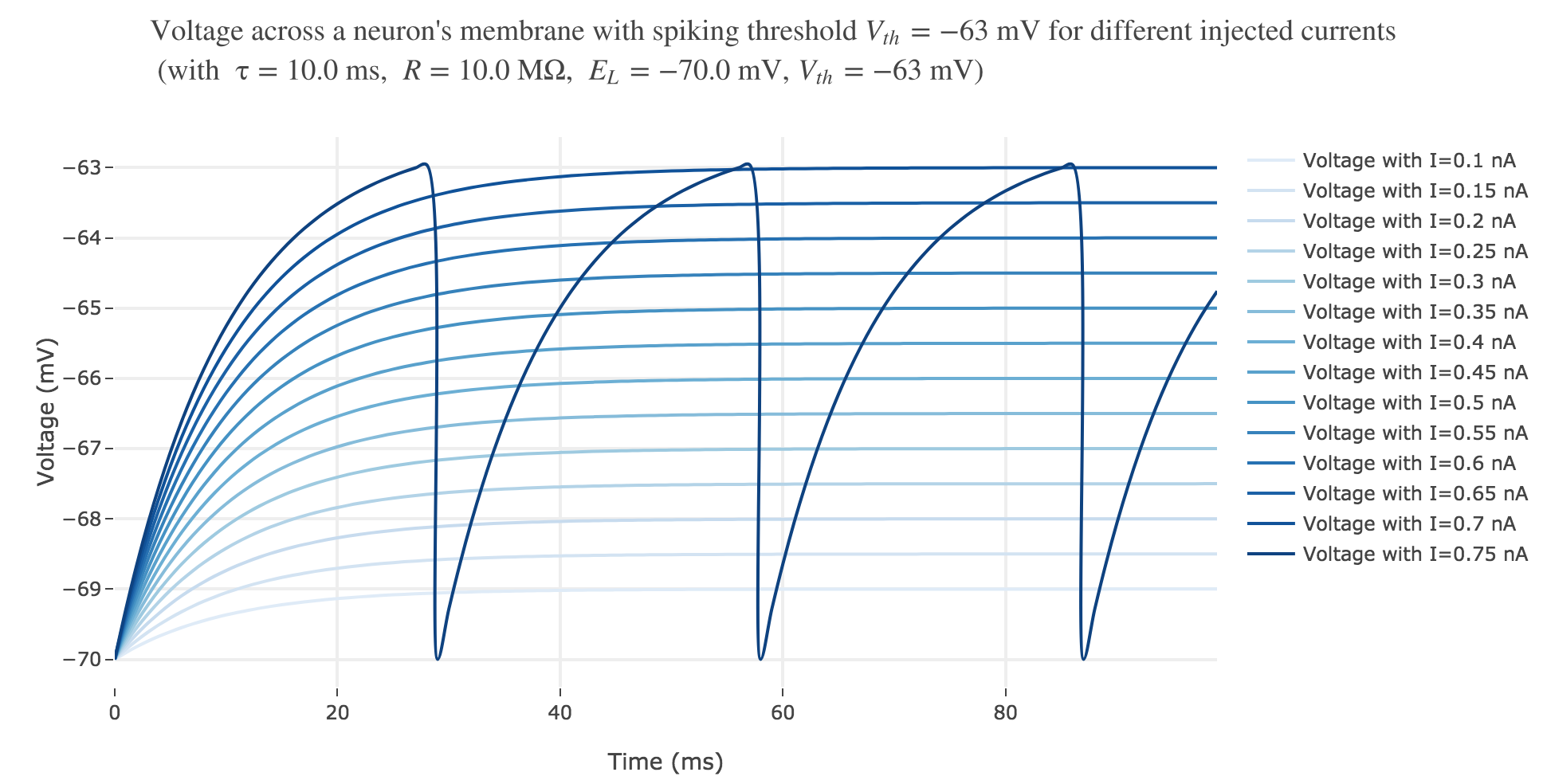
b). Let us now consider the case of a current step.
In this case, we turn on a current at time $t=t_0$ and then turn it off after $T$ time units. In other words, the current is given by:
\[I(t) = \begin{cases} 0 \text{ for } t<t_0 \\ I_0 \text{ for } t_0 ≤ t < t_0+T\\ 0 \text{ for } t ≥ t_0 + T \end{cases}\]How large does $I_0$ have to be, as a function of $T$, for the neuron to spike? Make a plot of $I_0$ versus $T$.
Analogously to what we did in the previous question, we can show that:
-
for $t ∈ [0, t_0]$:
\[V(t) = E_L + \text{const} × \e^{-t/τ}\]and since $V(0) = E_L$:
\[E_L = E_L + \text{const} \; ⟺ \; \text{const} = 0\]that is:
\[V(t) = E_L\] -
for $t ∈ [t_0, t_0+T[$:
\[V(t) = E_L + RI_0 + \text{const} × \e^{-t/τ}\]and since $V(t_0) = E_L$:
\[E_L = E_L + RI_0 + \text{const} × \e^{-t_0/τ} \; ⟺ \; \text{const} = - R I_0 \, \e^{t_0/τ}\]that is:
\[V(t) \, = E_L + R I_0 \left(1-\e^{-(t-t_0)/τ}\right)\] -
for $t ∈ [t_0+T, +∞[$:
\[V(t) = E_L + \text{const} × \e^{-t/τ}\]and since $V(t_0+T) = E_L + R I_0 \left(1-\e^{-T/τ}\right)$:
\[E_L + R I_0 \left(1-\e^{-T/τ}\right) = E_L + \text{const} × \e^{-(t_0+T)/τ} \; \\ ⟺ \; \text{const} = R I_0 \left(1 - \e^{-T/τ}\right) \e^{(t_0+T)/τ}\]that is:
\[V(t) \, = E_L + R I_0 \left(1-\e^{-T/τ}\right) \, \e^{-(t-t_0-T)/τ}\]
Thus:
-
for $t < t_0$, the membrane voltage is constant and equal to the equilibrium potential $E_L$
-
for $t_0 ≤ t < t_0+T$, the voltage increases up to $V(t_0 + T) = E_L + R I_0 \left(1-\e^{-T/τ}\right)$
-
for $t ≥ t_0 + T$, the voltage decreases to $\lim\limits_{t \to +∞} V(t) = E_L$
so the maximal value reached by $V$ is $V(t_0 + T) = E_L + R I_0 \left(1-\e^{-T/τ}\right)$
As a consequence, the neuron spikes if and only if:
\[\begin{align*} \quad & V(t_0 + T) = E_L + R I_0 \left(1-\e^{-T/τ}\right) ≥ V_{th} \\ ⟺ \quad & I_0 ≥ \frac{V_{th} - E_L}{R \left(1-\e^{-T/τ}\right)} \\ \end{align*}\]
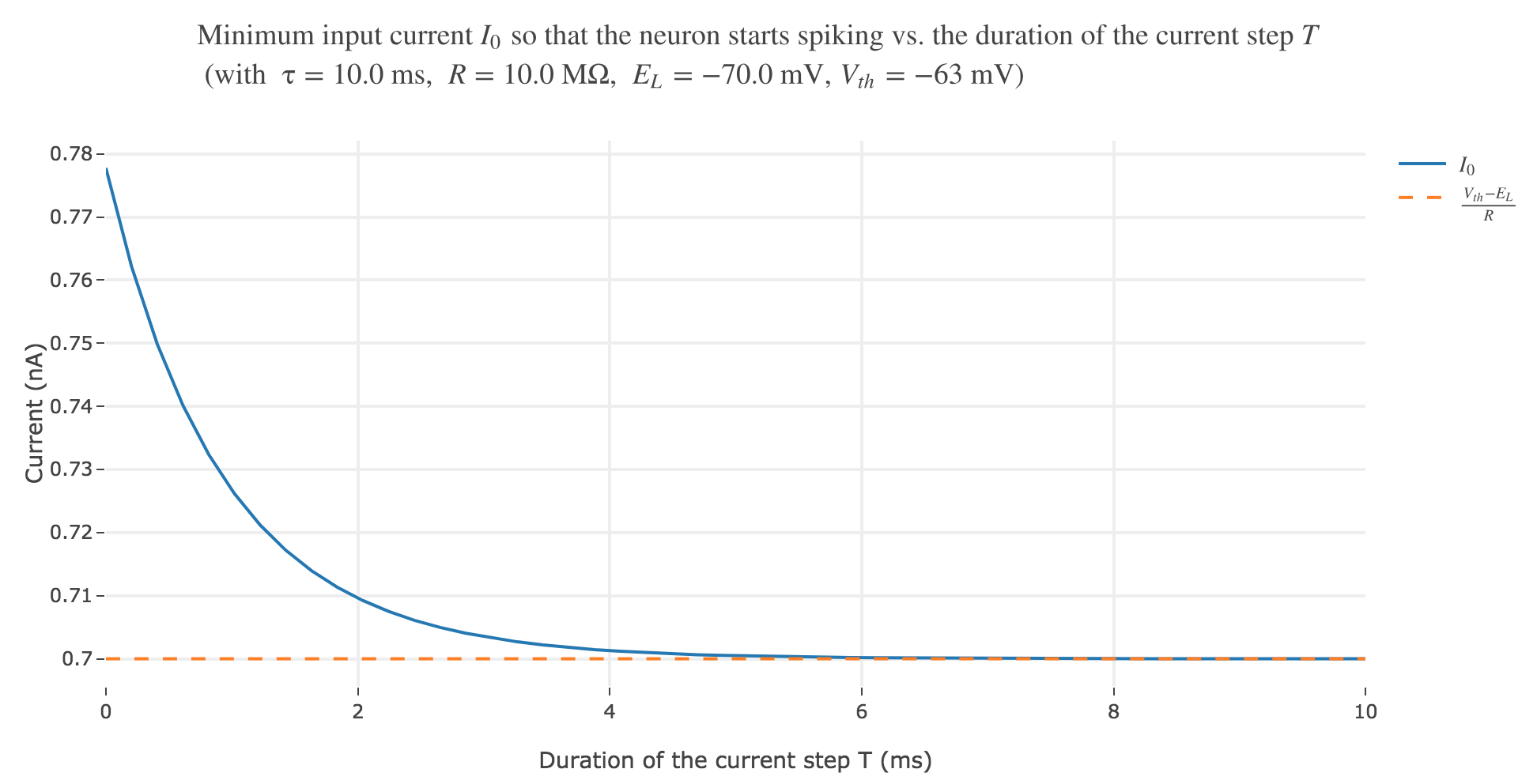
c. Advanced: Imagine that two current steps of length $T$ are injected with a time delay of $Δt$. What is the maximum delay $Δt$ between the two steps until an action potential is emitted?
Let us assume that the first current step happens between $t_0$ and $t_0+T$ as before: then the second current step occurs between $t_0+T+Δt$ and $t_0+2T+Δt$ as they are delayed by $Δt$.
Similarly to what we did in the previous question:
-
for $t ∈ [0, t_0]$:
\[V(t) = E_L\] -
for $t ∈ [t_0, t_0+T[$:
\[V(t) \, = E_L + R I_0 \left(1-\e^{-(t-t_0)/τ}\right)\] -
for $t ∈ [t_0+T, \, t_0 + T + Δt[$:
\[V(t) \, = E_L + R I_0 \left(1-\e^{-T/τ}\right) \, \e^{-(t-t_0-T)/τ}\] -
for $t ∈ [t_0+T+Δt, \, t_0 + 2T + Δt[$:
\[V(t) = E_L + RI_0 + \text{const} × \e^{-t/τ}\]and since $V(t_0 + T + Δt) = E_L + R I_0 \left(1-\e^{-T/τ}\right) \, \e^{-Δt/τ}$:
\[E_L + R I_0 \left(1-\e^{-T/τ}\right) \, \e^{-Δt/τ} = E_L + RI_0 + \text{const} × \e^{-(t_0+T+Δt)/τ} \\ ⟺ \; \text{const} = R I_0 \; \e^{(t_0+T+Δt)/τ} \left(\big(1-\e^{-T/τ}\big)\, \e^{-Δt/τ} -1\right)\]that is:
\[V(t) \, = E_L + R I_0 \Bigg(1 + \e^{-(t-t_0-T-Δt)/τ} \left(\big(1-\e^{-T/τ}\big)\, \e^{-Δt/τ} -1\right)\Bigg)\] -
for $t ∈ [t_0+2T+Δt, \, + ∞[$:
\[V(t) = E_L + \text{const} × \e^{-t/τ}\]and since $V(t_0+2T+Δt) = E_L + R I_0 \left(1 + \e^{-T/τ} \Big(\left(1-\e^{-T/τ}\right)\, \e^{-Δt/τ} -1\Big)\right)$:
\[E_L + R I_0 \left(1 + \e^{-T/τ} \Big(\left(1-\e^{-T/τ}\right)\, \e^{-Δt/τ} -1\Big)\right) = E_L + \text{const} × \e^{-(t_0+2T+Δt)/τ} \; \\ ⟺ \; \text{const} = R I_0 \, \e^{(t_0+2T+Δt)/τ} \; \left(1 + \e^{-T/τ} \Big(\left(1-\e^{-T/τ}\right)\, \e^{-Δt/τ} -1\Big)\right)\]that is:
\[V(t) \, = E_L + R I_0 \, \left(1 + \e^{-T/τ} \Big(\left(1-\e^{-T/τ}\right)\, \e^{-Δt/τ} -1\Big)\right) \, \e^{-(t-t_0-2T-Δt)/τ}\]
Thus:
-
for $t < t_0$, the membrane voltage is constantly equal to the equilibrium potential $E_L$
-
for $t_0 ≤ t < t_0+T$, the voltage increases up to $V(t_0 + T) = E_L + R I_0 \left(1-\e^{-T/τ}\right)$
-
for $t_0 + T ≤ t < t_0 + T + Δt$, the voltage decreases down to $V(t_0 + T + Δt) = E_L + R I_0 \left(1-\e^{-T/τ}\right) \, \e^{-Δt/τ}$
-
for $t_0 + T + Δt ≤ t < t_0 + 2T + Δt$, the voltage increases up to $V(t_0 + 2T + Δt) = E_L + R I_0 \left(1 + \e^{-T/τ} \Big(\left(1-\e^{-T/τ}\right)\, \e^{-Δt/τ} -1\Big)\right)$
-
for $t ≥ t_0 + 2T + Δt$, the voltage decreases to $\lim\limits_{t \to +∞} V(t) = E_L$
As
\[V(t_0 + 2T + Δt) = V(t_0 + T) + R I_0 \, \e^{-T/τ} \left(1-\e^{-T/τ}\right)\, \e^{-Δt/τ} > V(t_0 + T)\]the maximal value reached by $V$ is $V(t_0 + 2T + Δt)$.
As a consequence, the neuron spikes if and only if:
\[\begin{align*} \quad & V(t_0 + 2T + Δt) ≥ V_{th} \\ ⟺ \quad & E_L + R I_0 \left(1 + \e^{-T/τ} \Big(\left(1-\e^{-T/τ}\right)\, \e^{-Δt/τ} -1\Big)\right) ≥ V_{th}\\ ⟺ \quad & \e^{-T/τ} \Big(\left(1-\e^{-T/τ}\right)\, \e^{-Δt/τ} -1\Big) ≥ \frac{V_{th} - E_L}{R I_0} - 1\\ ⟺ \quad & \left(1-\e^{-T/τ}\right)\, \e^{-Δt/τ} ≥ \e^{T/τ} \, \left(\frac{V_{th} - E_L}{R I_0} - 1\right)+1\\ ⟺ \quad & Δt ≤ -τ \; \ln \frac{\e^{T/τ} \, \left(\frac{V_{th} - E_L}{R I_0} - 1\right)+1}{1-\e^{-T/τ}}\\ \end{align*}\]
2. Integrate-and-Fire with refractory period
Real neurons usually have refractory periods, i.e. for a few milliseconds after an action potential, the neuron will not fire again.
How could you add such a refractory period to the integrate-and-fire neuron?
To add a refractory period $Δ$, we make the voltage stay constant at the equilibirum potential $E_L$ for a time span $Δ$ whenever it is reset to $E_L$ after reaching the threshold.
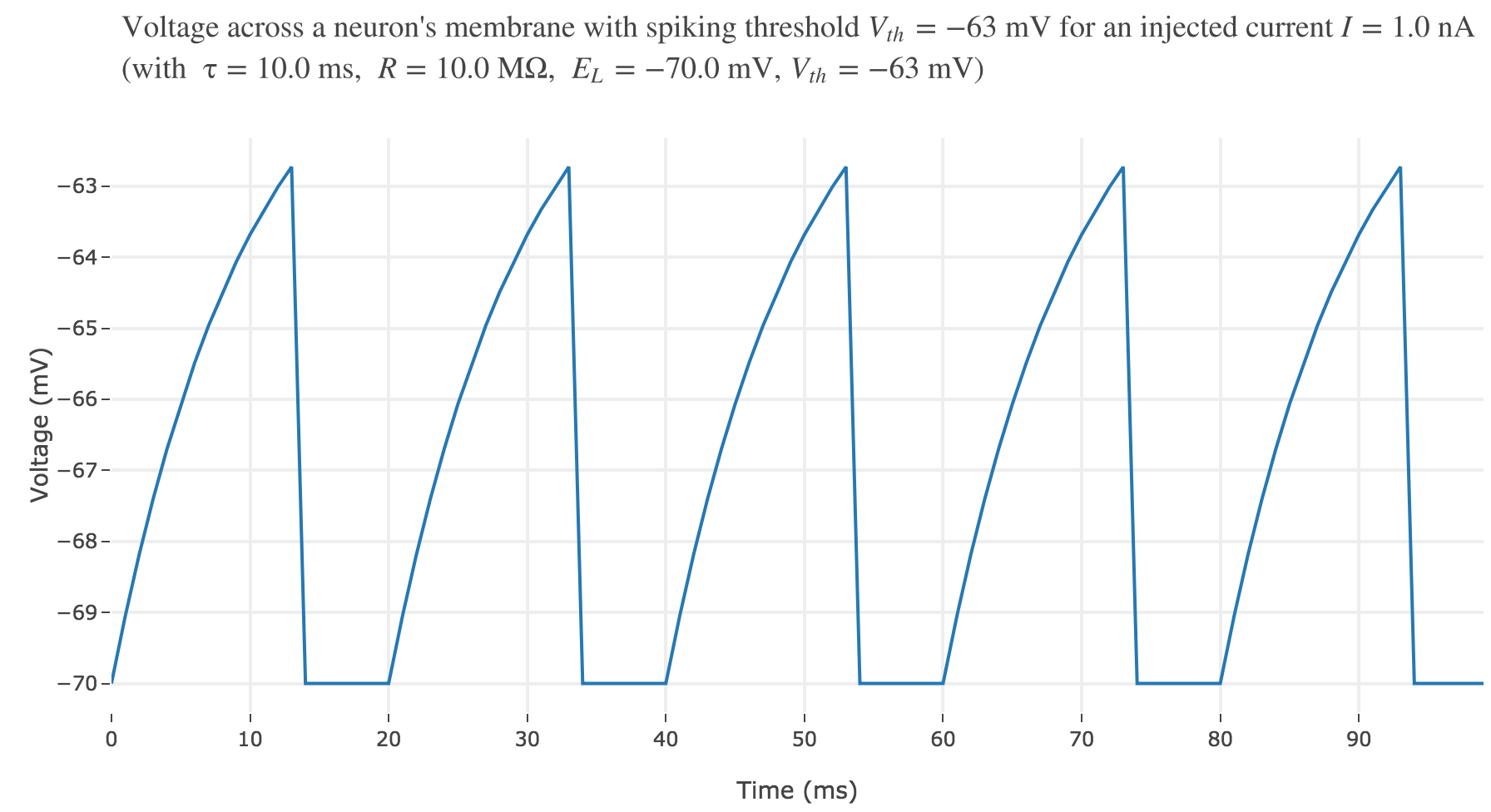
Compute the new $fI$-curve, i.e. the firing rate versus input current curve of the neuron with refractory period. How does it differ from the old one?
Let us denote by $T$ the time to threshold when there is no refractory period:
\[\begin{align*} \quad & τ \frac{\d V(t)}{\d t} = E_L - V(t) + RI(t) \quad \text{ and } \quad V(0) = E_L \\ ⟺ \quad & V(t) \, = E_L + R I_0 \left(1-\e^{-t/τ}\right) \\ \end{align*}\]and by definition of $T$:
\[\begin{align*} \quad & V(T) = V_{th} \\ ⟺ \quad & E_L + R I_0 \left(1-\e^{-T/τ}\right) = V_{th} \\ ⟺ \quad & \e^{-T/τ} = 1- \frac{V_{th} - E_L}{RI_0} \\ ⟺ \quad & T = - τ \, \ln\left(1- \frac{V_{th} - E_L}{RI_0}\right) \\ ⟺ \quad & T = τ \, \ln\left(\frac{RI_0}{RI_0 - V_{th} + E_L}\right) \\ \end{align*}\]and the firing rate $f$ is equal to:
\[f ≝ \frac 1 T = \left(τ \, \ln\left(\frac{RI_0}{RI_0 - V_{th} + E_L}\right)\right)^{-1}\]So when there is a refractory period $Δ$:
\[T_{ref} = τ \, \ln\left(\frac{RI_0}{RI_0 - V_{th} + E_L}\right) + Δ\]as a result of which the firing rate is equal to:
\[f_{ref} ≝ \frac {1} {T_{ref}} = \left(τ \, \ln\left(\frac{RI_0}{RI_0 - V_{th} + E_L}\right) + Δ\right)^{-1}\]
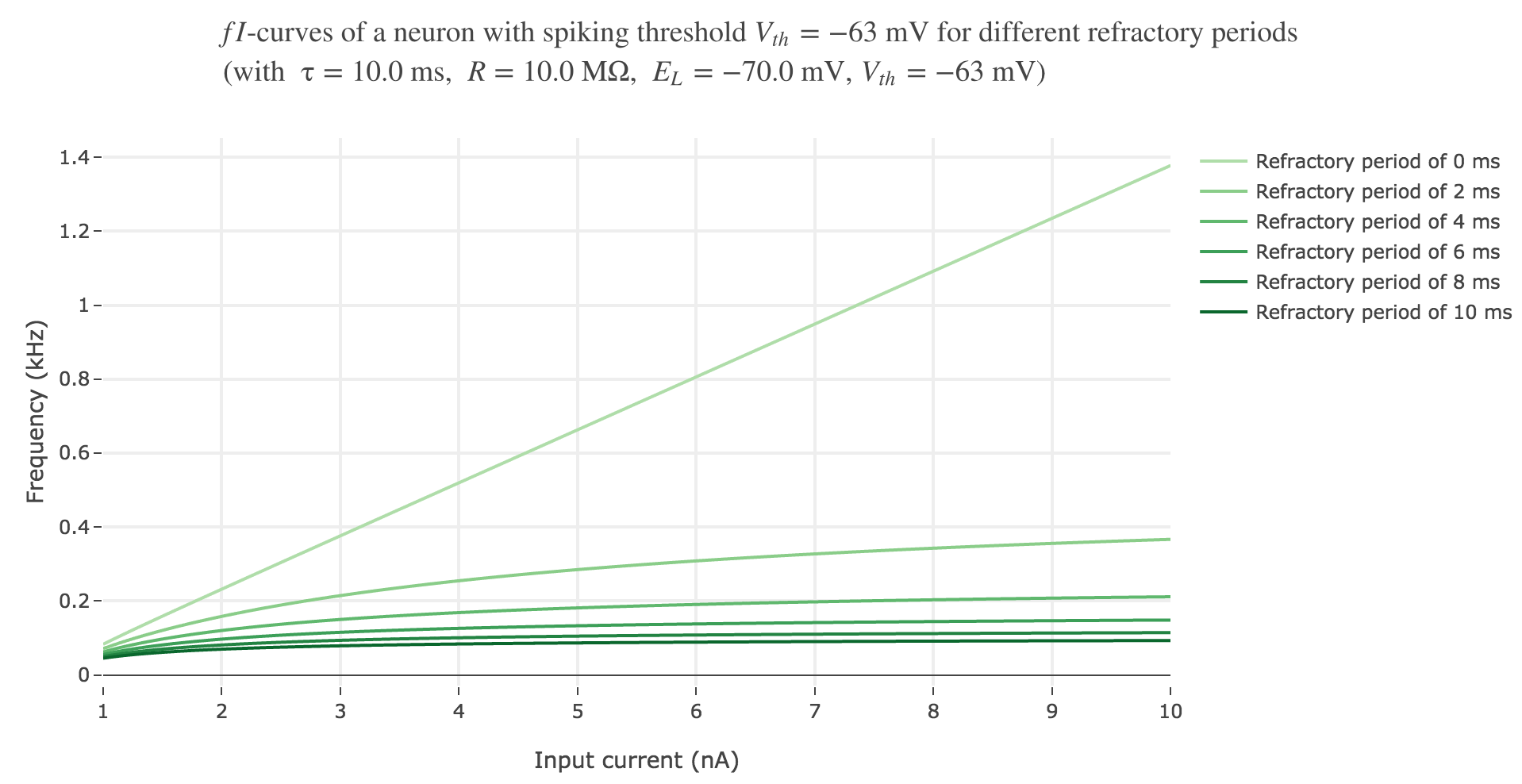
Therefore, compared to $f$:
-
the firing rate $f_{ref}$ is now bounded by $\frac{1}{Δ}$:
\[f_{ref} = \Bigg(\underbrace{τ \, \ln\left(\frac{RI_0}{RI_0 - V_{th} + E_L}\right)}_{≥ 0} + Δ\Bigg)^{-1} ≤ \frac{1}{Δ}\] -
and it is lower than the firing rate without refractory period $f$:
\[f_{ref} = \Bigg(τ \, \ln\left(\frac{RI_0}{RI_0 - V_{th} + E_L}\right) + \underbrace{Δ}_{≥ 0}\Bigg)^{-1} ≤ \frac{1}{τ \, \ln\left(\frac{RI_0}{RI_0 - V_{th} + E_L}\right)} = f\]
Leave a comment