TD2 : K plus proches voisins et validation croisée¶
Partie théorique : Non-consistance de la règle du plus proche voisin.¶
Comme dit dans le titre nous allons chercher à démontrer que la règle du 1 plus proche voisin n'est pas consistante au sens vu dans le cours. Dans tout cet exercice, on appelle risque le risque au sens de Vapnik défini par $R(f) = \mathbb{E}[\ell(f(X), Y)]$.
1 ) Rappelez la définition de la consistance d'une règle d'apprentissage de classifieur $\widehat{f}_n = \mathcal{A}(D_n)$ où $\widehat{f}_n: \mathbb{R}^d \longrightarrow \lbrace 0,1 \rbrace$.
- Observe data: $(x_i, y_i)_{1 ≤ i≤n} = D_n$
Consistance d'un classifieur:
$$𝔼(ℛ(\hat{f}_n)) ⟶_{n ∞} ℛ(f^\ast) ≝ \min_{f ∈ F} ℛ(f)$$
le classifieur empirique $ℛ(\hat{f}_n)$ dépend des données $D_n$
Cadre de l'exercice : On considère le cas de la classification binaire (le risque est donc le risque de la perte $0-1$) où l'on dispose d'un $n$-échantillon $D_n=(x_i,y_i)$ avec $\mathcal{X}=[0,1], \mathcal{Y}=\lbrace 0,1 \rbrace$.
Ce $n$-échantillon est généré de manière i.i.d. comme suit: les $x_i$ sont la réalisation (ou observation) de variables aléatoires $X_i$ suivant une certaine distribution $P$ admettant une densité $p$ par rapport à la mesure de Lebesgue sur $\mathcal{X}$. Les étiquettes $y_i$ sont la réalisation de variables aléatoires $Y_i$ distribuées en respectant $\forall x \in \mathcal{X},\eta(x)=\mathbb{P}(Y=1\vert X=x)=\alpha > \frac{1}{2}$.
A partir de ce $n$-échantillon, on construit un classifieur $\widehat{f}_n = \mathcal{A}(D_n)$. Il est important de garder à l'esprit que ce classifieur $\widehat{f}_n$ peut être vu comme la réalisation d'une variable aléatoire dépendant de $D_n = (X_1, \ldots, X_n, Y_1, \ldots, Y_n)$. Etudier la consistance de la régle de classification définie par $\widehat{f}_n$ revient à s'intéresser au comportement de la variable aléatoire $\widehat{f}_n$ quand $n$ tend vers l'infini.
2) En considérant la distribution des données décrite ci-dessus, donner l'expression du prédicteur de Bayes et le risque associé.
Prédicteur de Bayes pour les étiquettes $Y∈ \{1, \ldots, n\}$:¶
Classe prédite: $$i^\ast ≝ argmax_{1 ≤ i ≤n} P(Y=i \mid X=x)$$
Binaire: $Y ∈ \{0, 1\}$
$$i^\ast ≝ argmax_{1 ≤ i ≤ 2} P(Y=i \mid X=x)$$
But, comme $P(Y=1 \mid X=x)+ P(Y=2 \mid X=x) =1$
$$i^\ast = \begin{cases} 1 \text{ si } P(Y=1 \mid X=x) > 1/2 \\ 2 \text{ sinon}\end{cases}$$
Prédicteur de Bayes dans le cas de la classification binaire:
$$f^\ast(x) = 1_{η(x)>1/2} = \begin{cases} 1 \text{ si } P(Y=1 \mid X) ≥ 1/2\\ 0 \text{ sinon} \end{cases}$$
En l'occurrence: $η(x) = α > 1/2 ⟹ f^\ast = 1$, so:
Risque de Bayes:
$$ℛ(f^\ast) = 𝔼(1_{f(X) ≠ Y}) = P(Y ≠ 1) = P(Y ≠ 1 \mid X = x) = 1 - α$$
car $η(x) = α$ ne dépend pas de $X$, donc $P(Y=1) = P(Y=1 \mid X=x) = α$
3) On commence par considérer un classifieur quelconque $f$ qui ne dépend pas a priori de l'echantillon d'apprentissage $D_n$. Soit $X$ la variable aléatoire indépendante de $D_n$ qui intervient dans la définition du risque et qui correspond aux données de test. Montrer que le risque associé à $f$ peut s'exprimer comme (on remarquera qu'un classifieur binaire quelconque s'écrit $f(X)=\mathbb{1}_{\lbrace f(X)=1 \rbrace}$): $$R(f)=\alpha-(2 \alpha -1)\mathbb{E}_{X}[f(X)].$$
Risque d'un classifieur binaire:
$$ℛ(f) = 𝔼_{X, Y}(l(f(X), Y)) = 𝔼_{X, Y}(1_{f(X)≠Y}) = P_{X, Y}(f(X)≠Y)\\ = P_{X, Y}(f(X)=1, Y = 0) + P_{X, Y}(f(X)=0, Y = 1) \\ = P_{X, Y}(Y = 0) P(f(X) = 1) + P_{X, Y}(Y = 1)P_{X, Y}(f(X) = 0)$$
car $Y$ est indépendante de $X$ (et donc de $f(X)$ (lemme des coalitions))
Donc:
$$ℛ(f) = P(f(X) = 1) (1 - α)+ (1 - P(f(X) = 1)) α\\ = α - (2α -1) \underbrace{P(f(X) = 1)}_{𝔼(f(X))}$$
4) On considère maintenant le classifieur construit par la règle du plus proche voisin $\widehat{f}^1$, et on va démontrer qu'il n'est pas consistant.
a) Montrer que chaque variable aléatoire $Y_i$ est indépendante de $(X_1,\ldots, X_n)$ (on pourra se contenter d'une justification intuitive).
$Y_i$ indépendante de $(X_1, ⋯, X_n)$¶
$(X_i, Y_i)$ sont iid ⟹ $(X_i, Y_i)$ et $(X_j, Y_j)$ sont indépendantes si $i ≠ j$
Mais $Y_i$ est indépendante de $X_i$ ⟶ le résultat est acquis
b) En introduisant des variables $B_i(X)$ valant 1 si l'exemple $i$ de l'échantillon est le plus proche voisin de $X$ et 0 sinon, exprimez $\widehat{f}^1(X)$ comme une somme de variables aléatoires. Que vaut $\mathbb{E}_X[\sum^n_{i=1}B_i(X)|X_1, \ldots X_n]$ ?
$$\hat{f}^1(x) = \sum\limits_{ i =0 }^n Y_i B_i(x)$$
et $\sum\limits_{ i =0 }^n B_i(x) = 1$ car $x$ n'a qu'un voisin (puisque $X$ est à densité par rapport à la mesure de Lebesgue).
Remarque : il est naturel de se demander comment faire en pratique lorsqu'un point des données sur lesquelles on teste le classifieur est à égale distance de deux points d'apprentissage. Dans le formalisme de cet exercice, comme les variables ont une densité cela ne peut arriver qu'avec une probabilité nulle. En revanche, dans un contexte plus général, il est possible d'avoir avec une probabilité non nulle une nouvelle observation équidistante de deux points d'apprentissage. Plusieurs stratégies sont possibles: attribuer aléatoirement à la nouvelle observation le label de l'un ou l'autre des points dont elle est équidistant ou encore attribuer le label de l'observation de plus faible indice. % Quelle est la loi de $S$? Vérifiez que vous savez donner la variance et l'espérance associées.
c) Quelle est l'espérance de $Y_i$ conditionnellement à $(X_1,\ldots, X_n)$? Donnez l'expression de l'espérance de $\widehat{f}^1$ conditionnellement aux $(X_1, \ldots X_n)$ (l'espérance est prise par rapport à $X$ et aux $Y_i$).
Indépendance:
$$𝔼(Y_i \mid X_1, ⋯, X_n) = 𝔼(Y_i) = α$$
Donc
$$\begin{align*} 𝔼(\hat{f}(X) \mid X_1, ⋯, X_n) &= 𝔼(\sum\limits_{ i =0 }^n B_i(X) Y_i \mid X_1, ⋯, X_n) \\ &= \sum\limits_{ i =0 }^n 𝔼( B_i(X) Y_i \mid X_1, ⋯, X_n) \\ &= \sum\limits_{ i =0 }^n 𝔼( B_i(X) \mid X_1, ⋯, X_n) \underbrace{𝔼( Y_i \mid X_1, ⋯, X_n)}_{ ≝ α} &&\text{independence given } X_1, ⋯, X_n\\ &= α \underbrace{𝔼( \sum\limits_{ i =0 }^n B_i(X) \mid X_1, ⋯, X_n)}_{ = 1} \\ &= α \end{align*}$$
5) Donner le risque de $\widehat{f}^1$ et en déduire que la méthode des $1$-ppv n'est pas consistante.
Non-consistance:
$$𝔼_{D_n}(ℛ(\hat{f}_n)) \not⟶_{n ∞} ℛ^\ast$$
Par la question 3:
$$𝔼_{D_n}(ℛ(\hat{f}^1) = 2α(1-α) > 1-α \text{ if } α > 1/2$$
Donc $ℛ(\hat{f}^1) > ℛ^\ast$: pas consistant
6) On considère maintenant toujours le problème de classification binaire sur $\mathcal{X}$ avec le classifieur $\widehat{f}^K$ des $K$ plus proches voisins. Pour s'affranchir de certaines difficultés, on va supposer que $K$ est impair.
a) En vous inspirant du raisonnement précédent montrer que le risque du classifieur $\widehat{f}^K$ des $K$ plus proches voisins, conditionné sur les données d'entrainement $(X_1, \ldots X_n)$ (donc l'espérance du risque de $\widehat{f}^K$ pris par rapport aux seuls $Y_i$) peut s'exprimer en fonction de la probabilité pour une variable binomiale $U$ de paramètres $K$ et $\alpha$ d'être plus grande que $\frac{K}{2}$ (On rappelle que $U$ est une variable aléatoire binomiale de paramètre $\alpha$ et $K$ si $U$ peut s'écrire comme la somme de $K$ variables de Bernoulli de paramètre $\alpha$).
- $V_k(x)$: voisinage de $x$, i.e.: $$\lbrace i_1, ⋯, i_k \text{ s.t. } x_{i_1}, ⋯, x_{i_k} \text{ sont les plus proches de } x\rbrace$$
Règle de décision dans $k$-NN est un "vote":
$$\hat{f}^k ≝ 1_{\hat{η}^k(x) > 1/2}$$
où
$$\hat{η}^k(x) ≝ \frac 1 k \sum\limits_{ i ∈ V_k(x)} y_i$$
b) Montrer que l'espérance du risque associé au classifieur des $K$ plus proches voisins dans ce cas est strictement plus grand que le risque de Bayes $1-\alpha$. On pourra remarquer que l'espérance de $\widehat{f}^K$ est strictement plus petite que 1 par ce qui précède.
$$𝔼_{D_n} (ℛ(\hat{f}^k)) = α - (2α -1) 𝔼_{D_n} \underbrace{ 𝔼_X(\hat{f}^k \mid D_n)}_{> 1/2}$$
$$𝔼_X(\hat{f}^k \mid D_n) = 𝔼(1_{\hat{η}^k(X) > 1/2} D_n) \\ = P(\hat{η}^k(X) > 1/2 \mid D_n) \\ = P(\frac 1 k \sum\limits_{ i ∈ V_k(X) } y_i > 1/2 \mid D_n) \\ = P(\sum\limits_{ i ∈ V_k(X) } y_i > k/2 \mid D_n)$$
Comme $Y_i \sim B(α)$ (Bernoulli): $\sum\limits_{ i ∈ V_k(X) } y_i \sim B(α, k)$
$$𝔼(\hat{f}^k(X) \mid D_n) = P(Z > k/2) = β$$
où $Z \sim B(α, k)$ (binomiale)
Alors $𝔼(ℛ(\hat{f}^k(X))) = α - (2α -1) β > 1-α = ℛ(f^\ast)$
Conclusion: pas consistant
Morale de l'histoire De manière plus générale, il n'y a pas de choix universellement consistant du nombre de plus proches voisins, valable indépendamment du nombre de points dans l'ensemble d'entraînement. En revanche, il est possible de vérifier (en exercice à la maison par exemple) que si on considère une suite d'entiers $k_n$ telle que $\lim_{n\rightarrow \infty} k_n = \infty$ et $\lim_{n\rightarrow \infty} k_n/n = 0$ alors les hypothèses du théorème de Stone sont vérifiées pour toutes les distributions. Ainsi pour la suite de règles des $k_n$ plus proches voisins, on a la consistance universelle.*
Implémentation : K plus proches voisins et validation croisée¶
Pour ce TP on va utiliser des données réelles : des chiffres manuscrits, que vous pouvez télécharger à l'adresse http://www.math.ens.fr/cours-apprentissage/mnist_digits.mat.
Vous êtes censés les avoir déjà vues dans le TP d'intro à Python, je vous invite à retourner voir le notebook si vous avez oublié comment les charger / les manipuler.
Pour la classification avec $K$ classes, on appelle souvent matrice de confusion associée à des données $D_n=(x_t,y_t)$ la matrice $M \in \mathbb{N}^{K \times K}$ telle que $M_{i,j}$ soit le nombre d'éléments dont la vraie classe soit $i$ et dont la classe prédite par le classifieur $g$ soit $j$.
NB: Etant donné qu'il y a plus de $66000$ images dans le jeu de données, on va travailler avec un sous ensemble de ces $66000$ images afin de ne pas dépasser la mémoire disponible de votre ordinateur.
1) Commencez donc par reprendre contact avec les données. Elles sont composées d'un vecteur de labels y et d'images 28 pixels par 28 sous forme d'une matrice x de vecteurs linéarisés (chaque ligne de la matrice x correspond à une image).
a) Mettez quelques images sous forme matricielle avec reshape et affichez les.
import plotly
import numpy as np
import plotly.plotly as py
import plotly.graph_objs as go
import matplotlib.pyplot as plt
import scipy.io as sio
from scipy import stats
%matplotlib inline
plotly.offline.init_notebook_mode(connected=True)
from IPython.core.display import display, HTML
# The polling here is to ensure that plotly.js has already been loaded before
# setting display alignment in order to avoid a race condition.
display(HTML(
'<script>'
'var waitForPlotly = setInterval( function() {'
'if( typeof(window.Plotly) !== "undefined" ){'
'MathJax.Hub.Config({ SVG: { font: "STIX-Web" }, displayAlign: "center" });'
'MathJax.Hub.Queue(["setRenderer", MathJax.Hub, "SVG"]);'
'clearInterval(waitForPlotly);'
'}}, 250 );'
'</script>'
))
from scipy.io import loadmat
from numpy.random import randint
mnist = loadmat('mnist_digits.mat') # données sous forme de dictionnaire
nbr_img = 4 # nombre d'images à afficher
len_x = len(mnist['x'])
# Affichage de nbr_img images sélectionnées aléatoirement dans mnist['x']
for img in mnist['x'][randint(len_x, size=nbr_img), :]:
plt.figure()
plt.imshow(np.reshape(img, [28, 28]), interpolation="none")
b) Sélectionnez $6000$ images au hasard dans le jeu de données. Dressez un histogramme des classes pour vérifier que cette sélection n'a pas déséquilibré les classes (commande hist). Pour la suite on travaillera avec ce jeu de données restreint (cf remarque plus haut).
nbr_img = 6000 # nombre d'images à sélectionner au hasard
ind_rand = randint(len(mnist['x']), size=nbr_img) # indices des images sélectionnées
x, y = mnist['x'][ind_rand, :], mnist['y'][ind_rand] # images, labels
# Histogramme des labels
trace = go.Histogram(
x=y.flatten(),
xbins=dict(
start=-0.5,
end=9,
size=1
)
)
data = [trace]
layout = go.Layout(
title='Labels des images du jeu de données',
xaxis=dict(
title='Label'
),
yaxis=dict(
title='Nombre'
)
)
fig = go.Figure(data=data, layout=layout)
plotly.offline.iplot(fig)
c) Séparez les images en deux parties (dans les proportions $1/3,2/3$ par exemple) : un ensemble d'entraînement et un ensemble de test.
ind_train = range(0, int(1/3 * nbr_img))
ind_test = range(int(1/3 * nbr_img), nbr_img)
2) On va maintenant implémenter la règle de classification par plus proches voisins. Pour cela, vous pourrez avoir besoin de la fonction cdist du module scipy.spatial.distance. Cette fonction permet, étant donné deux matrices de design de calculer les distances euclidiennes au carré entre les points.
a) Ecrivez une fonction qui prenne en entrée le nombre de plus proches voisins désirés, les données d'entraînement et les données de test et ressorte la matrice de confusion sur l'ensemble de test.
Pour la matrice de confusion, on peut utiliser la commande confusion_matrix du module sklearn.metrics.
from scipy.spatial.distance import cdist
from sklearn.metrics import confusion_matrix
from collections import Counter
def confusion_kNN(k, x_train=x[ind_train, :], y_train=y[ind_train],
x_test = x[ind_test, :], y_test=y[ind_test]):
assert k>0
# fonction auxiliaire: prédiction du label (par vote majoritaire)
# en fonction des indices des plus proches voisins
def predicted_label(ind_neighbors):
# Conversion de l'array y_train[ind_neighbors] (contenant les
# labels des voisins d'entraînement) en tuple
label_neighbors = tuple(map(tuple, y_train[ind_neighbors]))
# élément majoritaire dans label_neighbors
return Counter(label_neighbors).most_common(1)[0][0]
# différences des distances 2 à 2 entre les images test et les images d'entraînement
dist_matrix = cdist(x_test, x_train, 'euclidean')
y_predicted = []
for i in range(len(x_test)):
# indices des k plus petites valeurs de dist_matrix[i, :]
# i.e. indices des k plus petites distances entre
# l'image-test d'indice i et les images d'entraînement
# i.e. indices des k images d'entraînement les plus proches
# de l'image-test i (par définition de dist_matrix)
ind_k_smallest = np.argpartition(dist_matrix[i, :], k)[:k]
y_predicted.append(predicted_label(ind_k_smallest))
return confusion_matrix(y_test, array(y_predicted))
print(confusion_kNN(1))
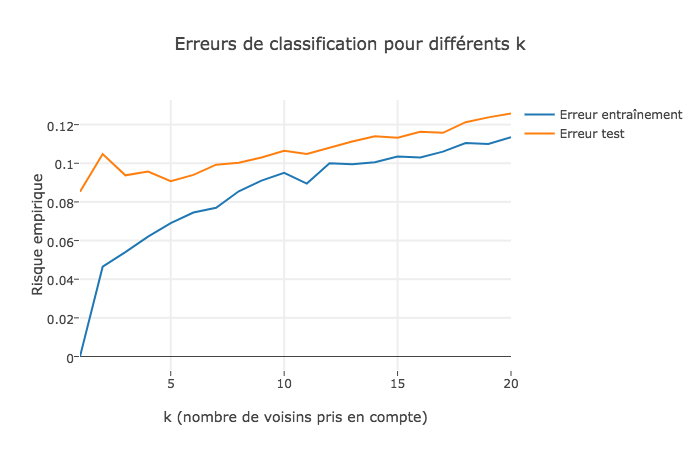
b) Affichez l'erreur de classification sur les ensembles d'entraînement et de test en fonction du nombre de $k$, nombre de plus proches voisins pris en compte (attention la complexité est décroissante avec le nombre de voisins pris en compte). Vous pouvez faire varier $k$ entre 1 et 20 par exemple.
k_max = 20
x_train = x[ind_train,:]
y_train = y[ind_train]
x_test = x[ind_test, :]
y_test = y[ind_test]
# détermination de l'erreur de classification
def classification_err(k_max=k_max, x_train=x_train, y_train=y_train, x_test=x_test, y_test=y_test):
# liste des erreurs de classification
err = []
for k in range(1, k_max+1):
# matrice de confusion à laquelle on enlève la diagonale
# (laquelle correspond aux prédictions correctes, dont la perte 0-1 vaut zéro)
confusion_err = confusion_kNN(k, x_train=x_train, y_train=y_train, x_test=x_test, y_test=y_test)
confusion_err -= np.diag(np.diag(confusion_err))
# calcul de l'erreur de prédiction
err.append(1. / len(x_test) * np.sum(confusion_err))
return array(err)
# Graphe: Risque empirique en fonction du paramètre k
# erreur sur l'ensemble d'entraînement (l'ensemble de test (en paramètre) est aussi l'ensemble d'entraînement)
trace_train_err = go.Scatter(x = list(range(1, k_max+1)), y = classification_err(x_test=x_train, y_test=y_train), mode = 'lines', name = 'Erreur entraînement')
# erreur sur l'ensemble de test
trace_test_err = go.Scatter(x = list(range(1, k_max+1)), y = classification_err(), mode = 'lines', name = 'Erreur test')
data_error = [trace_train_err, trace_test_err]
layout= go.Layout(
title= 'Erreurs de classification pour différents k',
hovermode= 'closest',
xaxis= dict(
title= 'k (nombre de voisins pris en compte)',
ticklen= 5,
zeroline= False,
gridwidth= 2,
),
yaxis=dict(
title= 'Risque empirique',
ticklen= 5,
gridwidth= 2,
),
showlegend= True
)
plotly.offline.iplot(go.Figure(data=data_error, layout=layout))
Exemple:¶
c) Séparez votre ensemble d'entraînement en un ensemble d'entraînement réduit et un ensemble de validation (on appelle en général cette technique la validation simple). En utilisant le code précédent, écrivez une fonction qui va utiliser l'ensemble de validation pour sélectionner le meilleur paramètre nombre de voisins $k$ au sens du nombre d'erreurs commises sur l'ensemble.
k_max = 20
prop = 1./3 # prop: proportion de l'ensemble d'entraînement réduit (1 - prop: proportion de l'ensemble de validation)
len_train = len(ind_train)
# fonction calculant le k qui minimise le nombre d'erreurs commises sur l'ensemble d'entraînement,
# lequel est séparé en:
# 1. un ensemble d'entraînement réduit (de proportion prop)
# 2. un ensemble de validation (de proportion 1-prop)
def choose_best_k(k_max=k_max, prop=prop, x_train=x_train, y_train=y_train):
len_train = len(x_train)
# permutation aléatoire des données d'entraînement
perm = np.random.permutation(len_train)
# Séparation en ensemble d'entraînement réduit et ensemble de validation
x_red, x_valid = np.split(x_train[perm], (int(prop*len_train),))
y_red, y_valid = np.split(y_train[perm], (int(prop*len_train),))
err = classification_err(k_max=k_max, x_train=x_red, y_train=y_red, x_test=x_valid, y_test=y_valid)
return np.argmin(err)+1
d) Séparez plusieurs fois de manière aléatoire votre ensemble d'entraînement. L'estimateur du nombre de plus proches voisins est il stable ?
k_max = 20
nbr_iter = 10 # nombre d'itérations de la procédure (de séparation de l'ensemble d'entraînement)
# liste des k minimisant l'erreur commise, pour chaque ensemble d'entraînement séparé
best_k = []
for _ in range(nbr_iter):
# proportion de l'ensemble d'entraînement réduit aléatoire (prop=rand())
best_k.append(choose_best_k(k_max=k_max, prop=rand()))
# Histogramme des k minimisant le nombre d'erreurs sur l'ensemble de vérification
# (pour chaque itérations de la procédure de séparation de l'ensemble d'entraînement)
trace = go.Histogram(
x=best_k,
xbins=dict(
start=-0.5,
end=k_max,
size=1
)
)
data = [trace]
layout = go.Layout(
title='Paramètre k minimisant le nombre d\'erreurs, sur {} ensembles d\'entraînement séparés aléatoirement'.format(nbr_iter),
xaxis=dict(
title='k'
),
yaxis=dict(
title='Nombre de fois meilleur paramètre'
)
)
fig = go.Figure(data=data, layout=layout)
plotly.offline.iplot(fig)
Exemple:¶
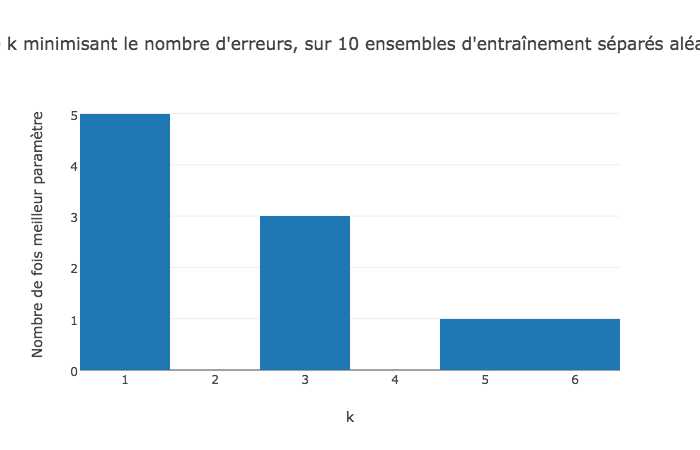
L'estimateur du nombre de plus proches voisins n'est pas stable
l'ensemble des valeurs de $k$ prises (dans l'exemple ci-dessus) vaut $\lbrace 1, 3, 5, 6\rbrace$
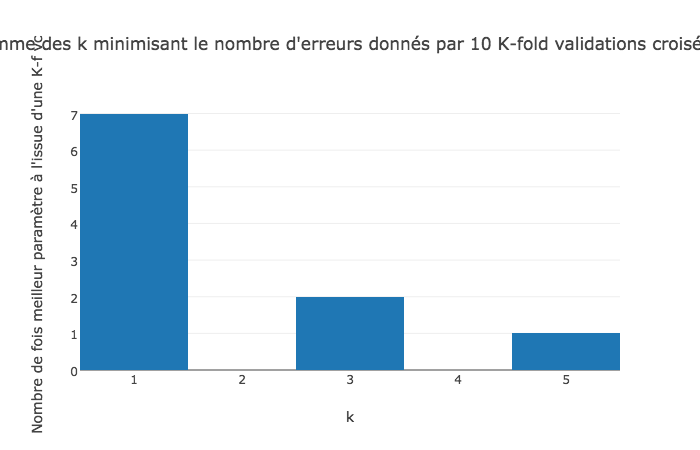
3) On souhaite désormais sélectionner le nombre de plus proches voisins optimal par validation croisée. Vous allez, en utilisant les données d'entraînement implémenter la technique de la K-fold validation croisée pour K=8. Faites le partitionnement des données d'entraînement plusieurs fois de manière aléatoire et regardez le comportement du nombre de plus proches voisins sélectionné. Que remarquez vous ?
K = 8
k_max = 20
nbr_iter = 10 # nombre d'itérations de la technique de K-fold validation croisée
def k_fold_validation(k_max=k_max, K=K, x_train=x_train, y_train=y_train):
len_train = len(x_train)
# permutation aléatoire des données d'entraînement
perm = np.random.permutation(len_train)
# partition de l'ensemble d'entraînement en K parties
partition_x = array(np.split(x_train[perm], K))
partition_y = array(np.split(y_train[perm], K))
# meilleurs k (minimisant l'erreur sur l'ensemble de vérification)
# pour la K-fold validation croisée courante
best_k = []
for i in range(K):
# Séparation en ensemble de validation (une des K parties, tour à tour)
# et ensemble d'entraînement réduit (les K-1 autres parties de la partition)
x_valid, x_red = partition_x[i], np.concatenate(partition_x[np.arange(K) != i])
y_valid, y_red = partition_y[i], np.concatenate(partition_y[np.arange(K) != i])
err = classification_err(k_max=k_max, x_train=x_red, y_train=y_red, x_test=x_valid, y_test=y_valid)
best_k.append(np.argmin(err)+1)
# on retourne le k majoritaire, parmi les meilleurs k
return Counter(best_k).most_common(1)[0][0]
# k retournés par les différents appels de k_fold_validation()
best_of_best_k = []
for _ in range(nbr_iter):
best_of_best_k.append(k_fold_validation())
# Histogramme des k minimisant le nombre d'erreurs sur les ensembles de vérification
# (pour toutes les K-fold validations croisées (tous les appels de k_fold_validation())
trace = go.Histogram(
x=best_of_best_k,
xbins=dict(
start=-0.5,
end=k_max,
size=1
)
)
data = [trace]
layout = go.Layout(
title='Histogramme des k minimisant le nombre d\'erreurs donnés par {} K-fold validations croisées (K={})'.format(nbr_iter,K) ,
xaxis=dict(
title='k'
),
yaxis=dict(
title='Nombre de fois meilleur paramètre à l\'issue d\'une K-f vc'
)
)
fig = go.Figure(data=data, layout=layout)
plotly.offline.iplot(fig)
nbr_img = 6000 # nombre d'images à sélectionner (pas au hasard, pour pouvoir comparer avec LDA et QDA)
ind_train = range(0, int(1/3 * nbr_img))
ind_test = range(int(1/3 * nbr_img), nbr_img)
file =
np.save(outfile, x)