I. Introduction
Théorème principal
Article fondateur (1986):
-
premier pas pour poser les bases d’une théorie des transformations d’objets
-
démontre un théorème d’existence de mouvement en contact
Ce que nous avons vu en cours sous la forme:
“Dès qu’il y a un chemin dans l’espace libre, il y a un chemin au contact”.
Théorème principal (Hopcroft & Wilfong):
Il existe mouvement de rotations et de translations entre 2 configurations où les objets forment une composante connexe,
⟹ il existe un mouvement entre ces 2 configurations tel qu’à tout instant, les objets forment une composante connexe.
De l’importance de la contractilité
L’espace des configurations n’est pas contractile
⟹ le théorème ne s'applique pas
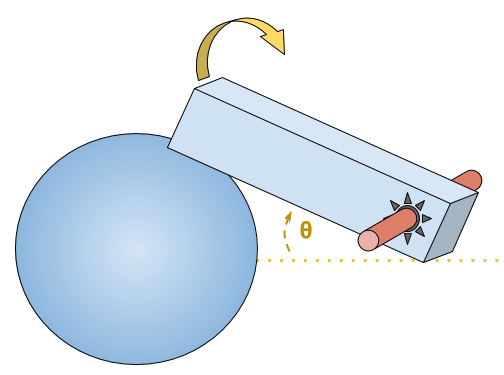
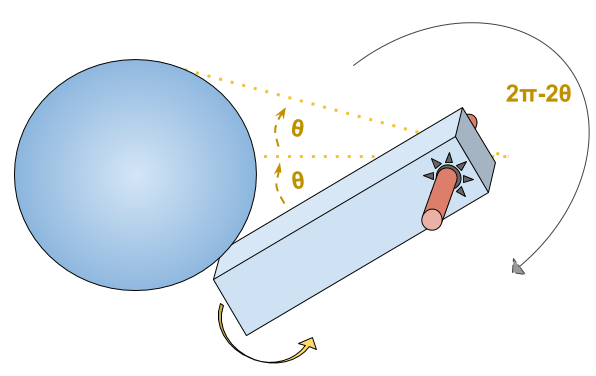
Espace des configurations
-
Objet: partie de $ℝ^n$
- convexe
- compacte
- égale à l’adhérence de son intérieur
- bornée par un nombre fini de surfaces algébriques
- Origine ⟶ position/l’orientation
-
Objet composé:
- plusieurs sous-objets ⟶ graphe des sous-objets sont qui s’intersectent
- base: son origine = celle de l’objet composé
-
Configuration: est un vecteur de position et d’orientation des objets
- ⟶ espace de configuration
- $B(x)$ / $b(x)$
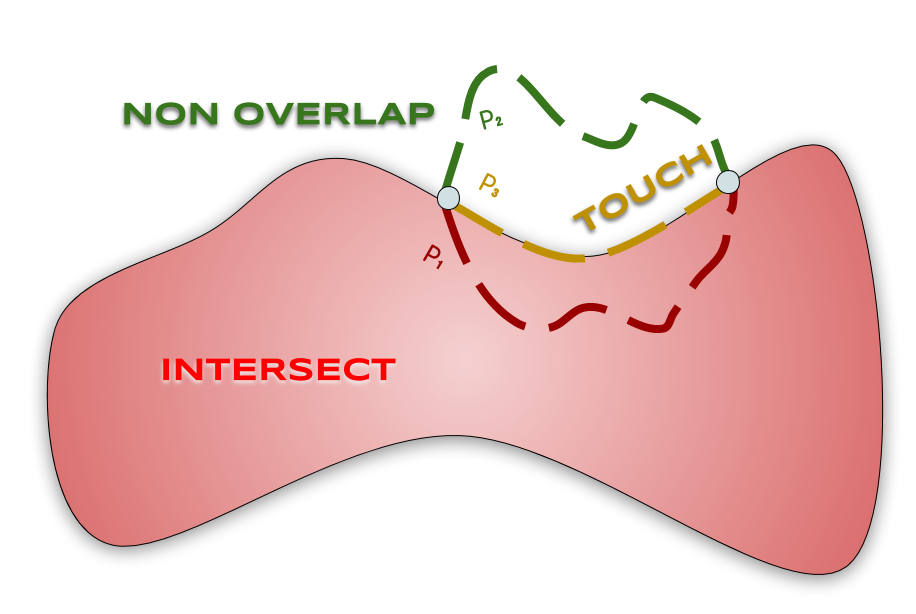
Intersection, Chevauchement, Toucher
Si $x$ est une configuration, on dit que deux objets $B_i, B_j$:
| s'*intersectent* en $x$ | si $B_i(x) ∩ B_j(x) ≠ ∅$ |
| se *chevauchent* en $x$ | si $\int(B_i(x)) ∩ \int(B_j(x)) ≠ ∅$ |
| se *touchent* en $x$ | si $B_i(x) ∩ B_j(x) ≠ ∅ ∧ \int(B_i(x)) ∩ \int(B_j(x)) = ∅$ |
Ensembles de configurations
| Ensemble | Configurations $x$ en lesquelles |
|---|---|
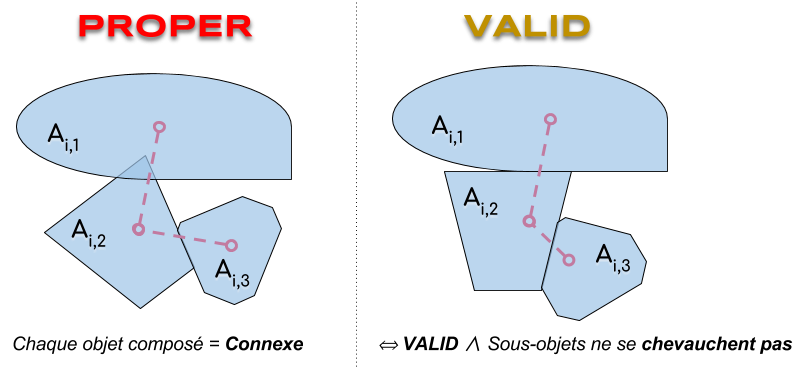
| PROPER | chaque objet composé a un graphe associé connexe (objets composés connexes et configurations propres) |
| VALID | chaque objet composé est connexe et est tel que tous les sous-objets qui s’intersectent se touchent (configurations valides) |
| Ensemble | Configurations $x$ valides telles qu’il existe (au moins) deux objets |
|---|---|
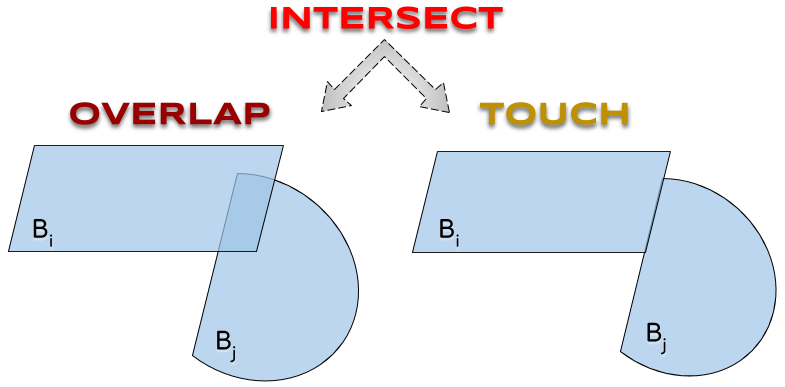
| INTERSECT | qui s’intersectent en $x$ |
| OVERLAP | qui se chevauchent en $x$ |
| TOUCH | qui se touchent en $x$ |
| Ensemble | Configurations $x$ propres telles que |
|---|---|
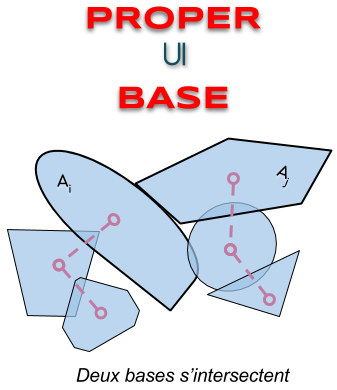
| BASE | la base d’un objet composé intersecte la base d’un autre |
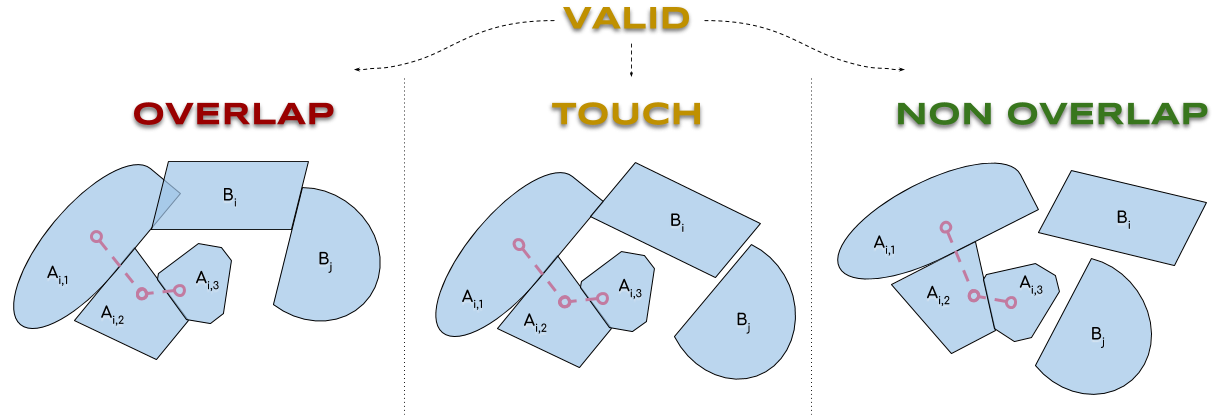
Enfin, on pose \(\NON ≝ \VALID\backslash\OVER \\ \FILL ≝ \cl(\OVER) ∪ \BASE\)
Pourquoi ?: En ajoutant $\BASE \not⊆ \VALID$ à $\cl(\OVER)$, on rend \(\NON ∪ \FILL\\ = \NON ∪ \cl(\OVER) ∪ \BASE\) contractile.
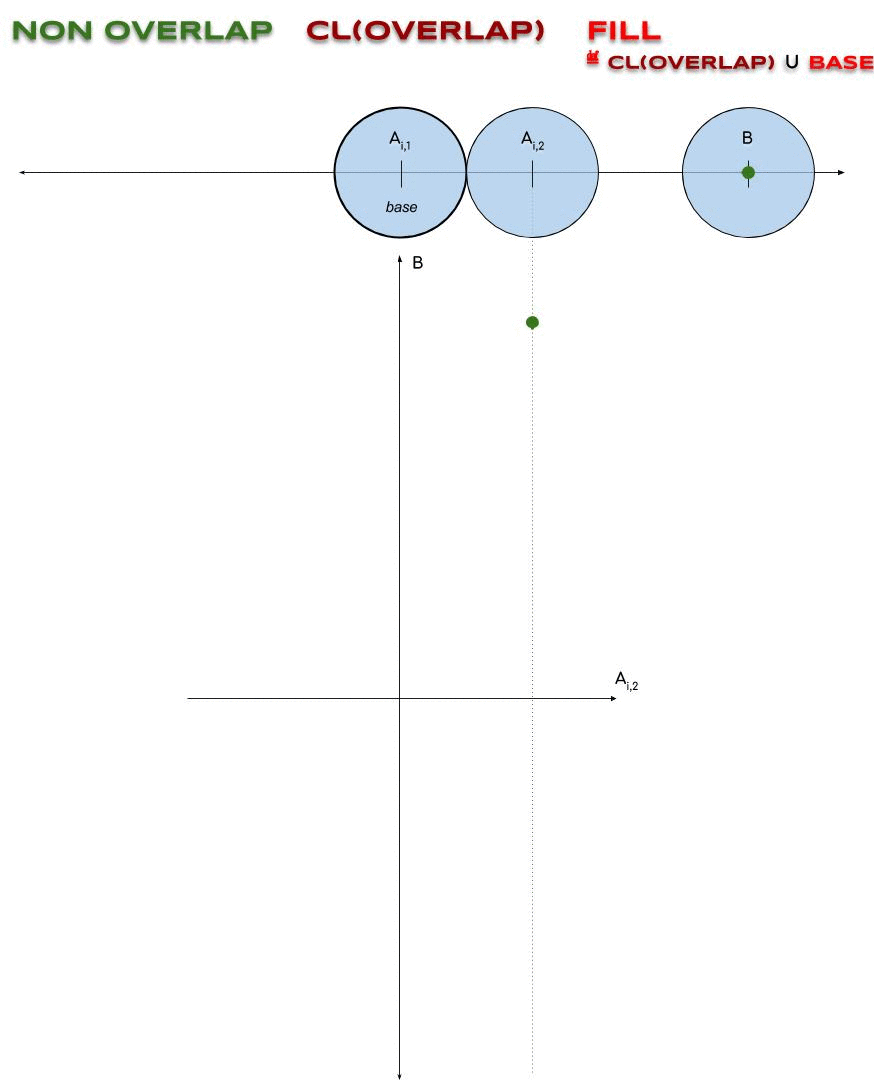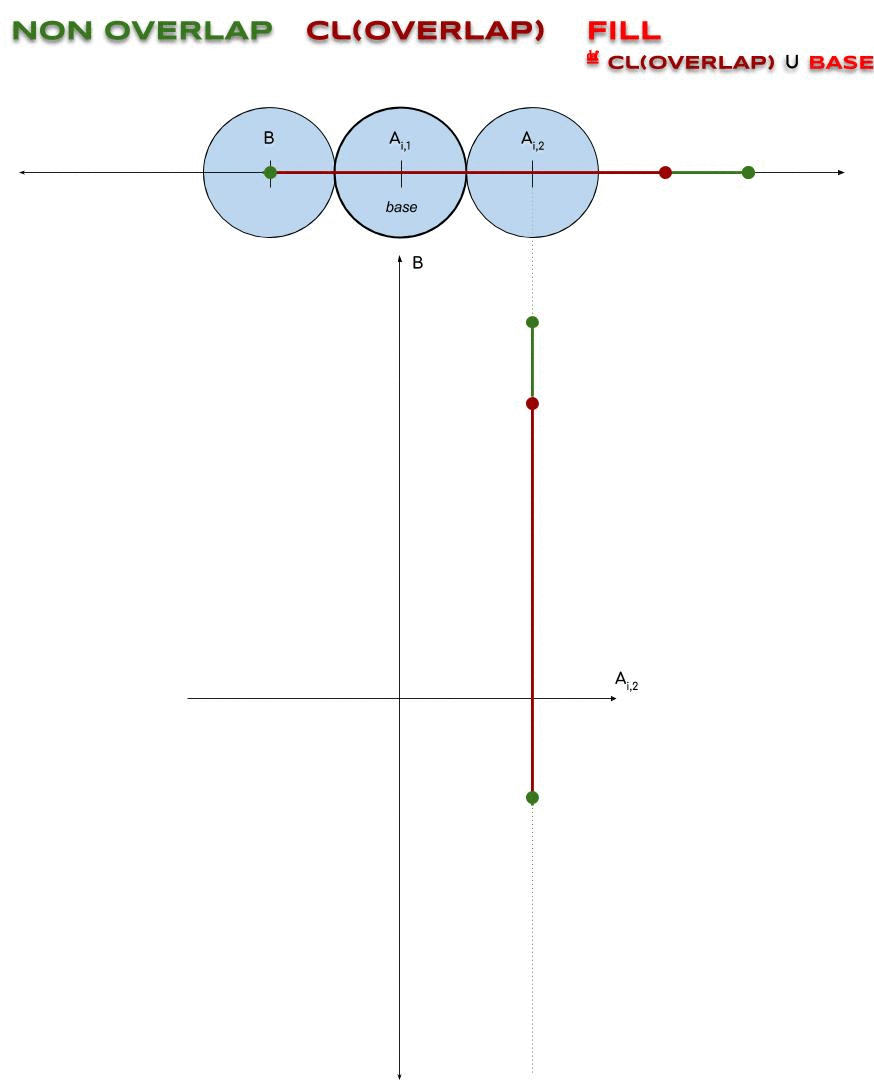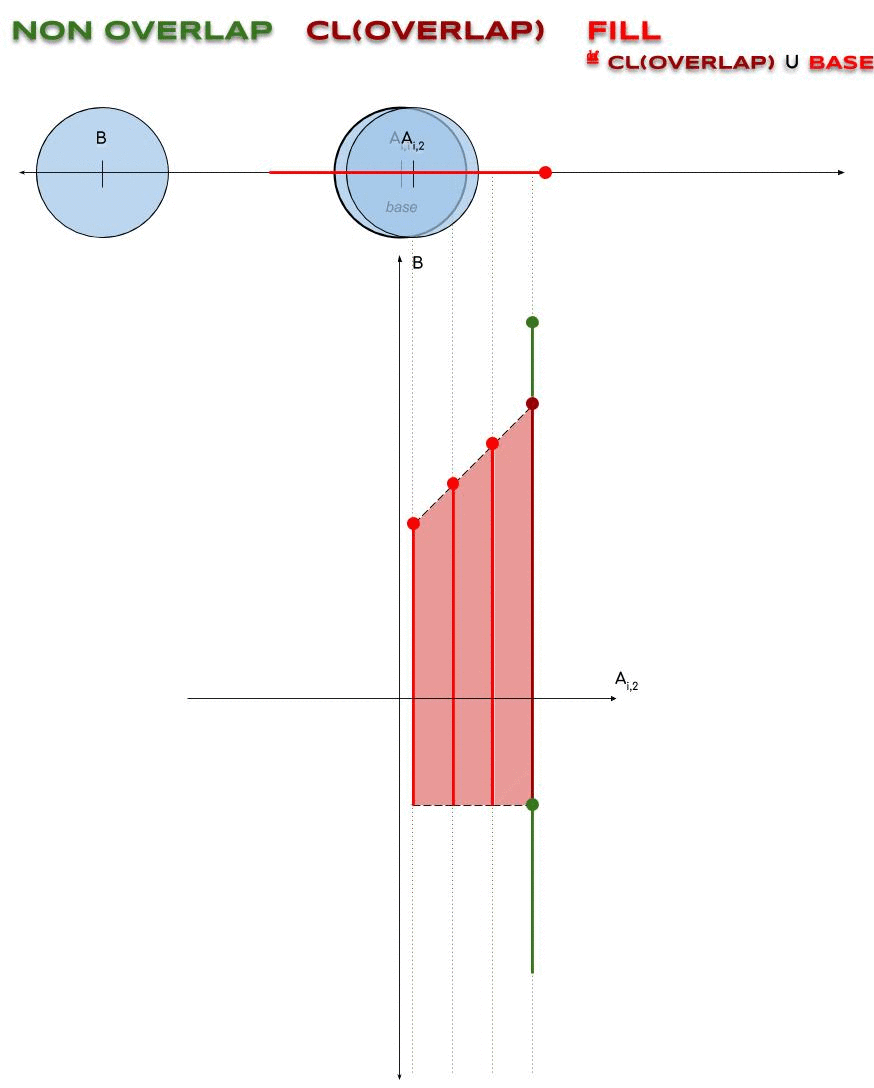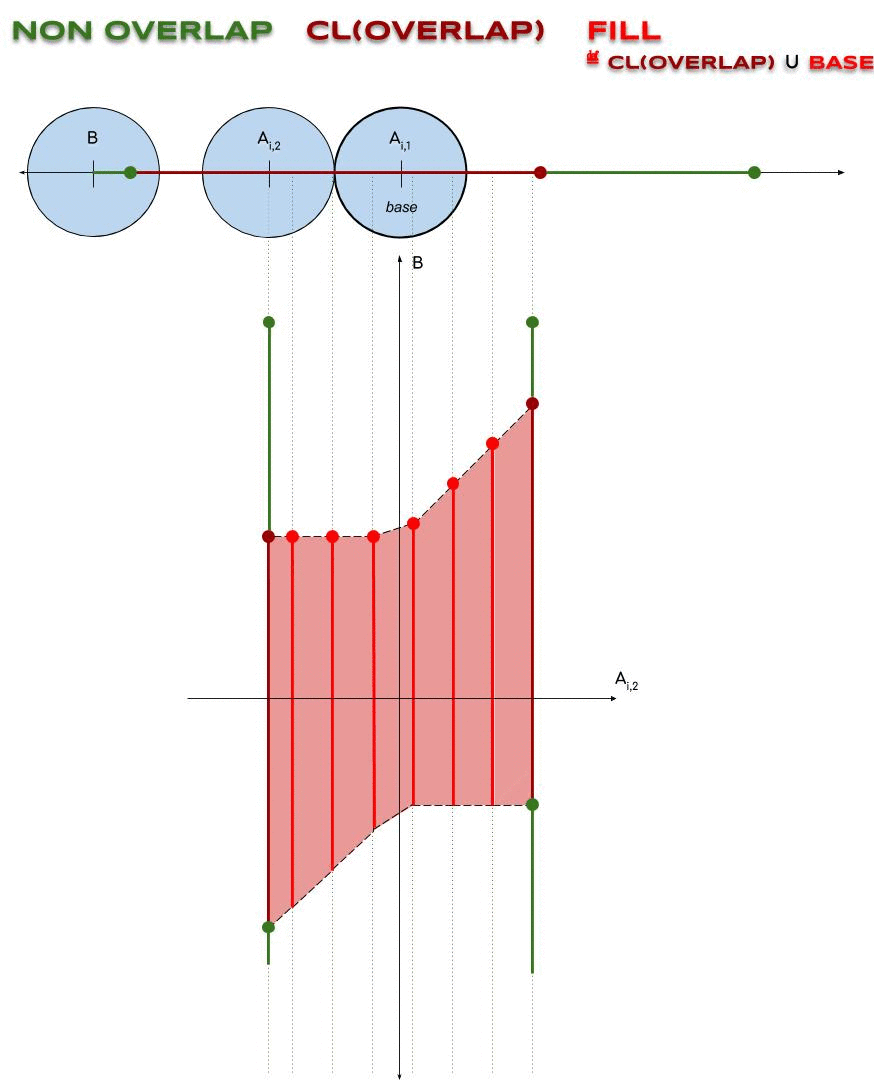 </div>
</div>
Détermination de TOUCH
Attention avec TOUCH

\[\TOUCH = \NON ∩ \cl(\OVER)\]
Esquisse de preuve:
-
Objets sont
- égaux à l’adhérence de leur intérieur (pour $⊆$) - de même pour les composés, car $\cl(\int(\bu))$ préseve l’union finie
- compacts (pour $⊇$)
⟹ on montre que \(\underbrace{\left\lbrace x \mid ∃i≠ j. \overbrace{A_i}^{\llap{\text{objet composé}}}(x) ∩ \overbrace{A_j}^{\rlap{\text{objet composé}}}(x) ≠ ∅ \right\rbrace}_{\text{noté } \INTp \not⊆ \VALID} = \cl\Bigg(\underbrace{\left\lbrace x \mid ∃i≠ j. \int(A_i(x)) ∩ \int(A_j(x)) ≠ ∅ \right\rbrace}_{\text{noté } \OVERp \not⊆ \VALID}\Bigg)\)
Par fermeture de $\VALID$:
\[\cl\Big(\underbrace{\OVER}_{≝\, \OVERp ∩ \VALID}\Big) = \cl(\OVERp) ∩ \VALID\]Et enfin
\[\begin{align*} \TOUCH & = \OVERp^c ∩ \INTp ∩ \VALID\\ &= \OVERp^c ∩ \VALID ∩ \INTp ∩ \VALID\\ & = \underbrace{\OVERp^c ∩ \VALID}_{ = (\OVERp ∪ \VALID)^c ∩ \VALID \, =\, \NON} ∩ \cl(\OVER) \\ & = \NON ∩ \cl(\OVER) \end{align*}\]Puis, comme
\[\BASE ∩ \NON ⊆ \TOUCH\]\[\TOUCH = \FILL ∩ \cl(\OVER)\]
Connexité et contractilité
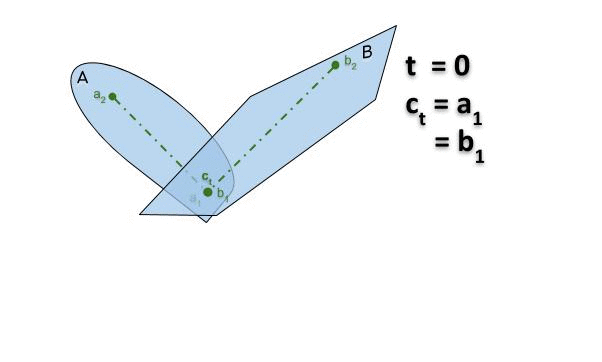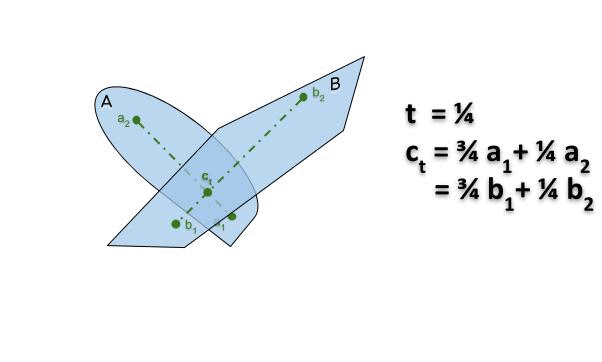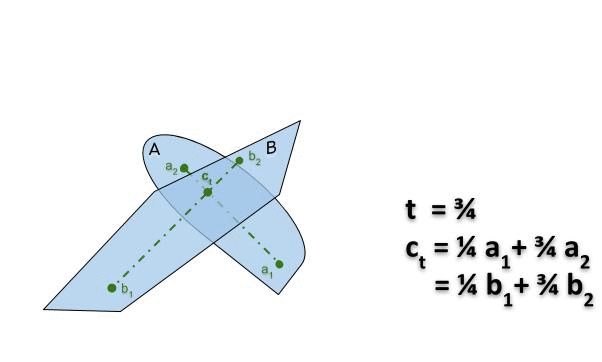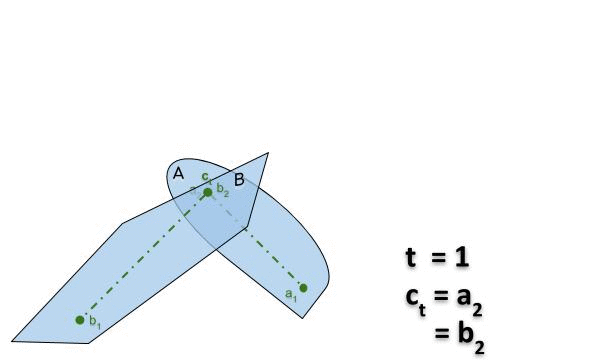
Connexité par arcs
BASE et FILL sont connexes par arcs
Lemme: De toute configuration dans VALID (resp. BASE), il existe un chemin dans VALID (resp. BASE) vers une configuration dans BASE où les origines des objets composés coïncident.
Corollaire: \(\FILL ∪ \NON = \BASE ∪ \VALID\) est contractile (et donc connexe par arcs)
Mayer-Vietoris
La suite suivante est exacte:
\[\begin{align*} H_1(\FILL ∪ \NON) &{\xrightarrow {\partial _{*}}}\,H_0(\FILL ∩ \NON)\\ &{\xrightarrow {(i_{*},j_{*})}}\,H_0(\FILL)\oplus H_0(\NON) \\ & {\xrightarrow {k_{*}-l_{*}}}\,H_0(\FILL ∪ \NON) \\ & {\xrightarrow {\partial _{*}}}\, \lbrace 0 \rbrace \end{align*}\]
où $i, j, k, l$ sont les inclusions, $\partial _{*}$ est défini à partir de l’opérateur bord
Intuitivement:
- l’homologie est l’ensemble des invariants topologiques de $X$, indiqués par des groupes d’homologie
- le $k$-ième groupe d’homologie $H_{k}(X)$ a autant de copies de $ℤ$ que $X$ contient de “trous” de dimension $k$
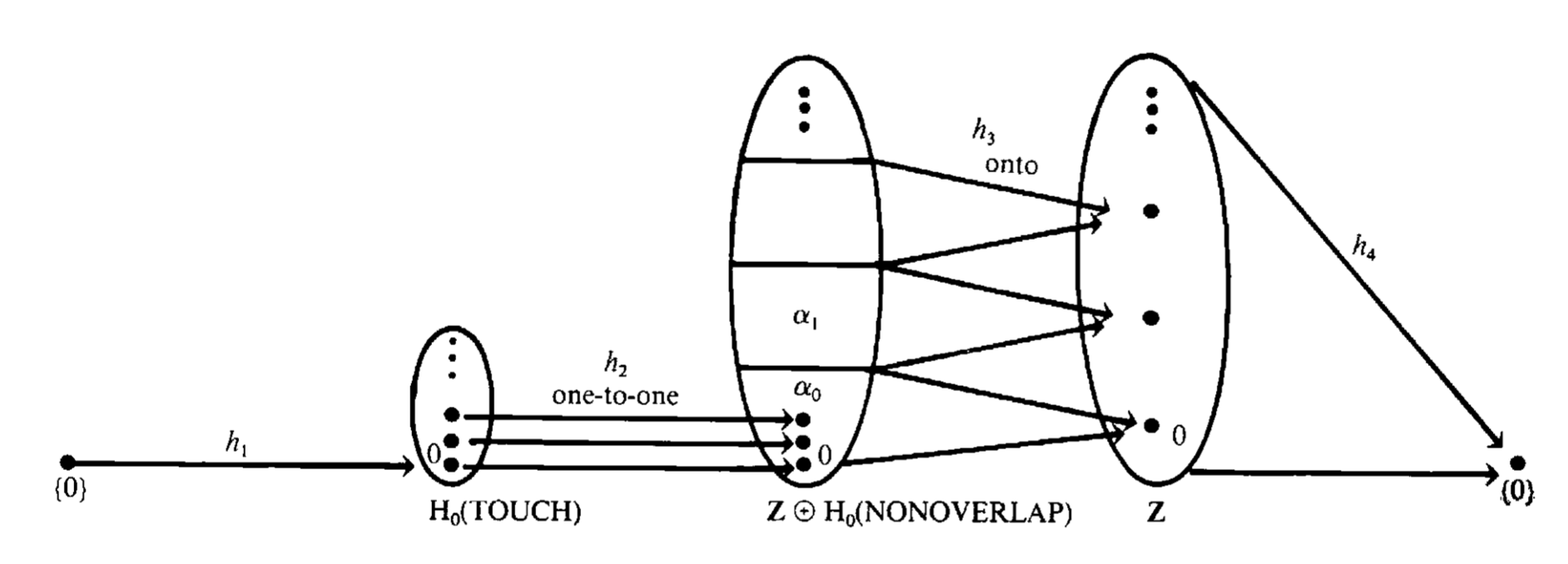
Il vient que:
\[\Big(\underbrace{H_0(\FILL)}_{≃ ℤ}\oplus H_0(\NON)\Big)/\underbrace{\Im (i_{*},j_{*})}_{≃ \,H_0(\TOUCH)} \\≃ H_0(\FILL ∪ \NON) ≃ ℤ\] \[⟹ H_0(\NON) ≃ H_0(\TOUCH)\]
Puis, on déduit que chaque composante connexe de $\NON$ contient une et une seule composante connexe de $\TOUCH$
