Memory Evolutive Neural Systems
When Category Theory meets Neuroscience
Younesse Kaddar
Based on A. Ehresmann and J.-P. Vanbremeersch’s work
Introduction: what’s wrong with biological systems?
I. Complex objects as colimits
II. Emergence theorem
III. Memory Evolutive Neural Systems
Introduction
- Memory Evolutive Systems:
- Categorical modelisation of hierarchical, evolving and self-regulating systems (≃ 30 years of research already!).
Authors
| A. Ehresmann |
 |
Mathematician (Université de Picardie):
|
| J.-P. Vanbremeersch |
 |
Physician (Université de Picardie): specialty in geriatry |
What’s wrong with biology?
1. Emergence vs. Reductionism

2. Self-organisation
-
Flexibility
-
Adaptability
I. Make room for… Category theory!
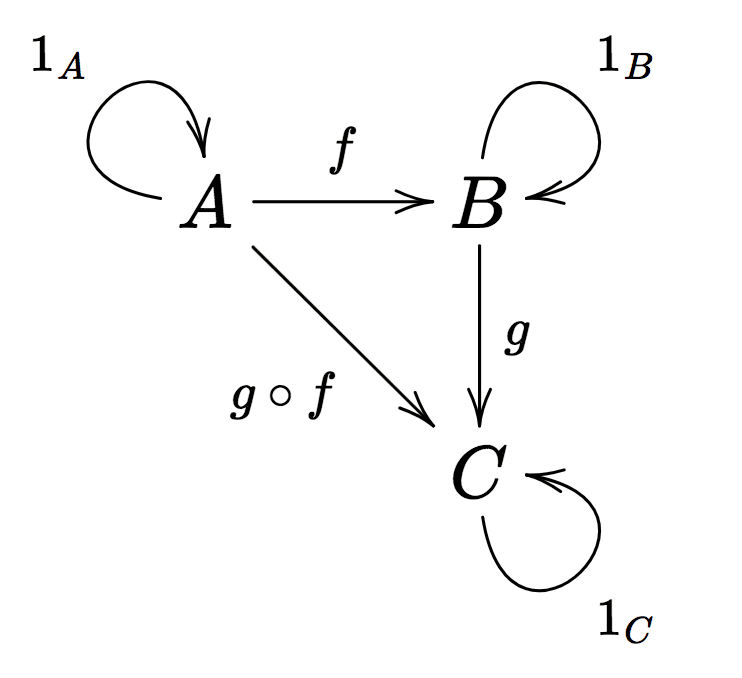
Structures preserved by morphisms$\qquad \overset{\text{+ associativity, identity}}{\rightsquigarrow} \qquad \underbrace{\text{Category Theory}}_{\text{focus on relations rather than objects}}$
Examples:
-
Objects preserved by morphisms:
- Sets
- Vector spaces, Topological spaces, Manifolds, Groups, Rings, …
- Logical formulas, Types (λ-calculus), …
-
Structures forming one category:
- Posets, Monoids, Groups, Groupoids, …
… and even (small) categories themselves form a category!
- Objects: Categories
- Morphisms: Functors

Universal constructions
- Limits:
-
-
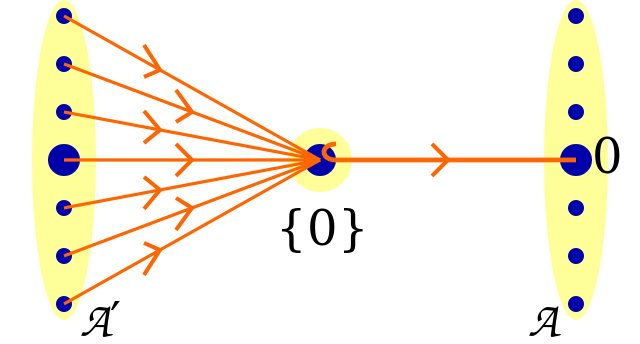
Terminal objects
-
Products
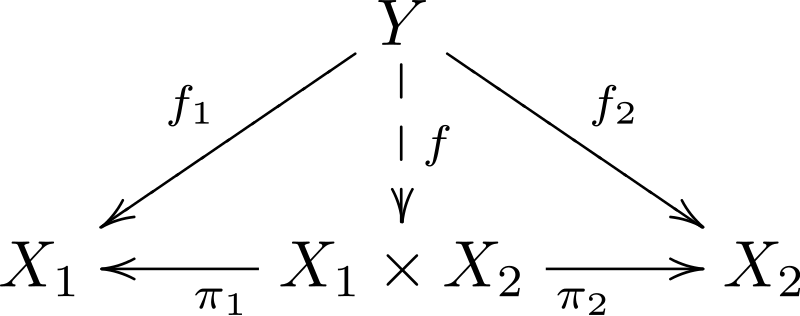
-
Equalizers (Kernels), Pullbacks, …
-
- Colimits:
-
-
Initial objects
-
Coproducts
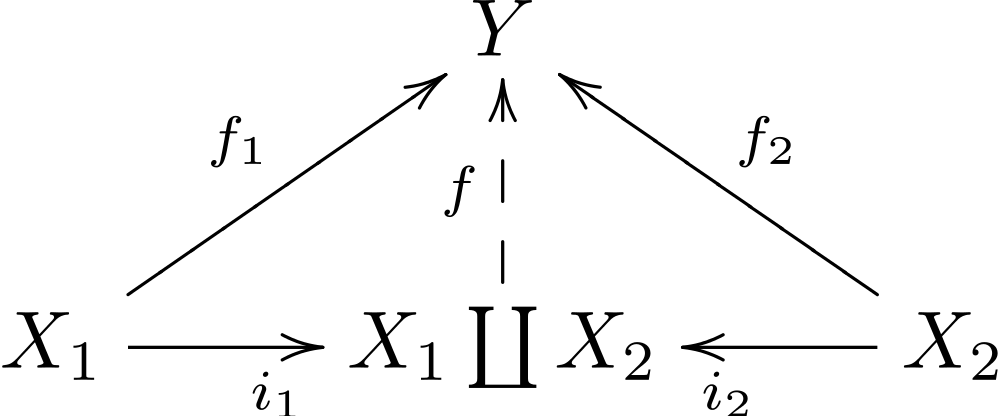
-
Coequalizers (Quotients), Pushouts, …
-
⟹ Colimits are more than sums
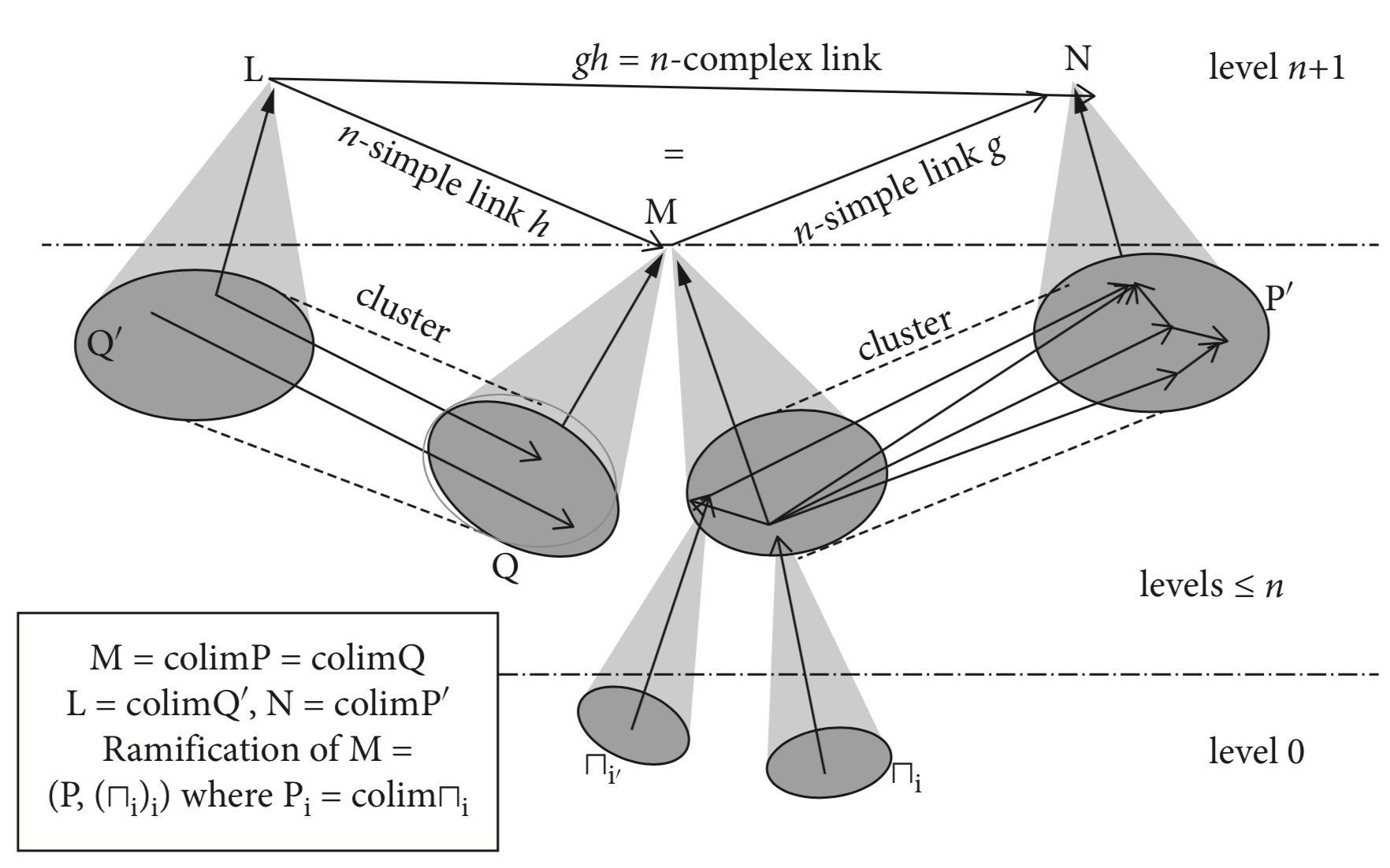
Complex objects as colimits
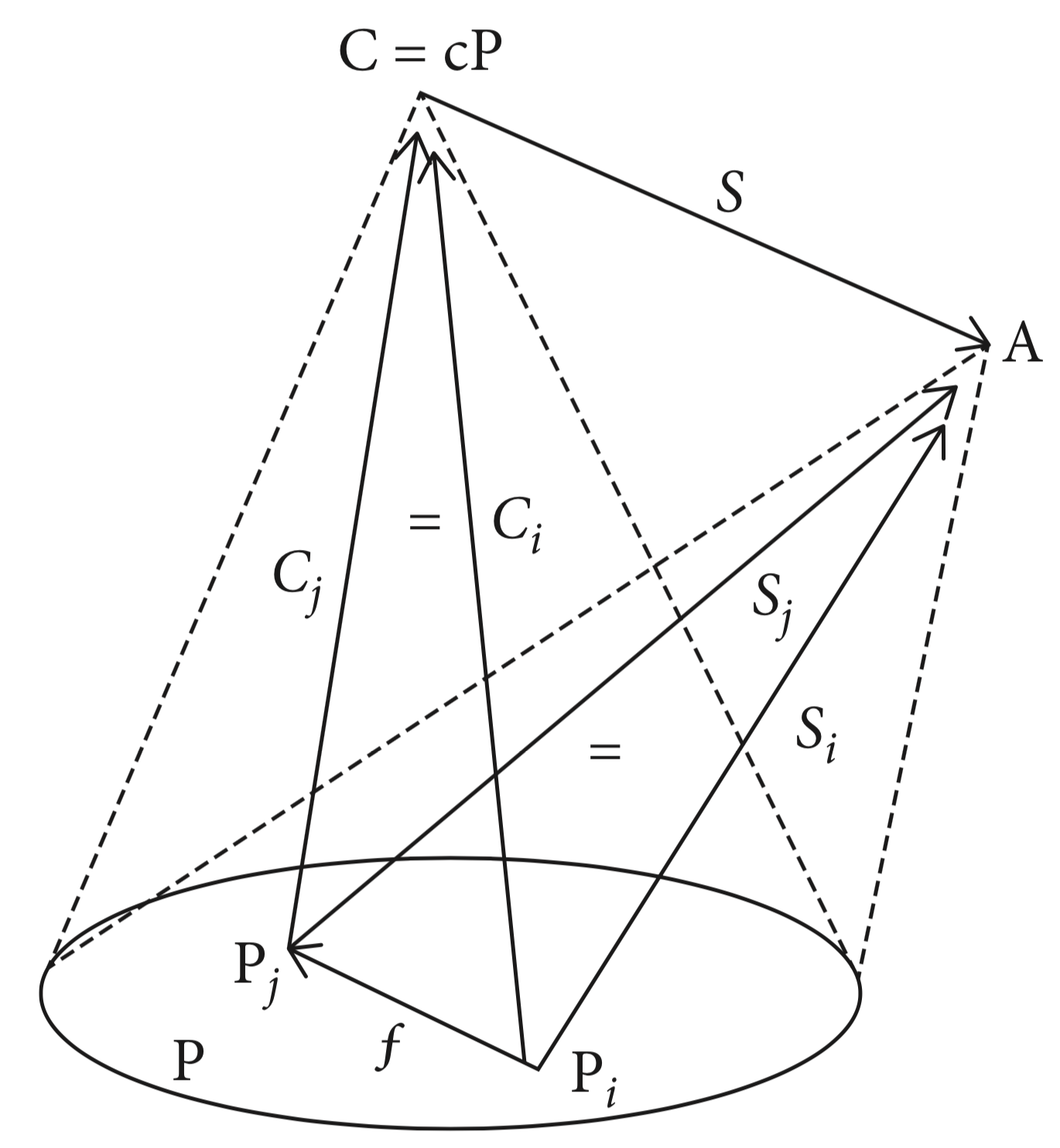
Hierarchical category $H_t$: layers of complexity: objects at level $n$ are colimits of patterns of level $<n$
II. Hierarchical Evolutive Systems (HES)
- Hierarchical Evolutive System (HES) $K$:
-
- a timescale $T ⊆ ℝ_+$
- $∀ t∈ℝ_+$, a hierarchical category $K_t$ (configuration at $t$)
- $∀ t < t'$, a transition functor $k_{tt'}: K_{tt'} ⊆ K_{t} ⟶ K_{t'}$
- Transitivity condition: a component $C ∈ H$ is a maximal set of objects linked by transitions.
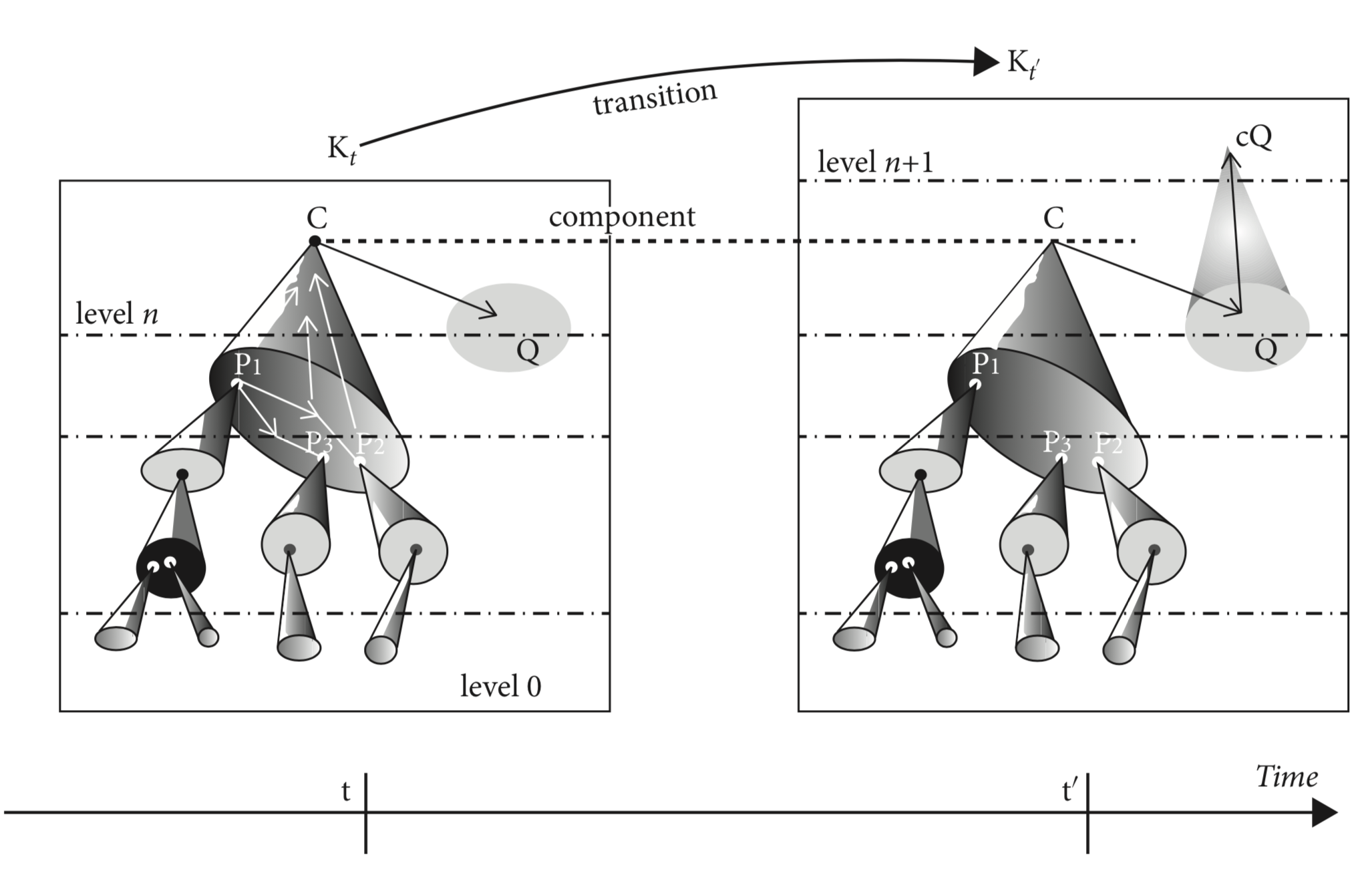
3. Multiplicity Principle
Multiplicity Principle: for each time and each level, there is at least one multi-faceted component, i.e. two patterns with the same colimit that are not isomorphic in the category of patterns and clusters.
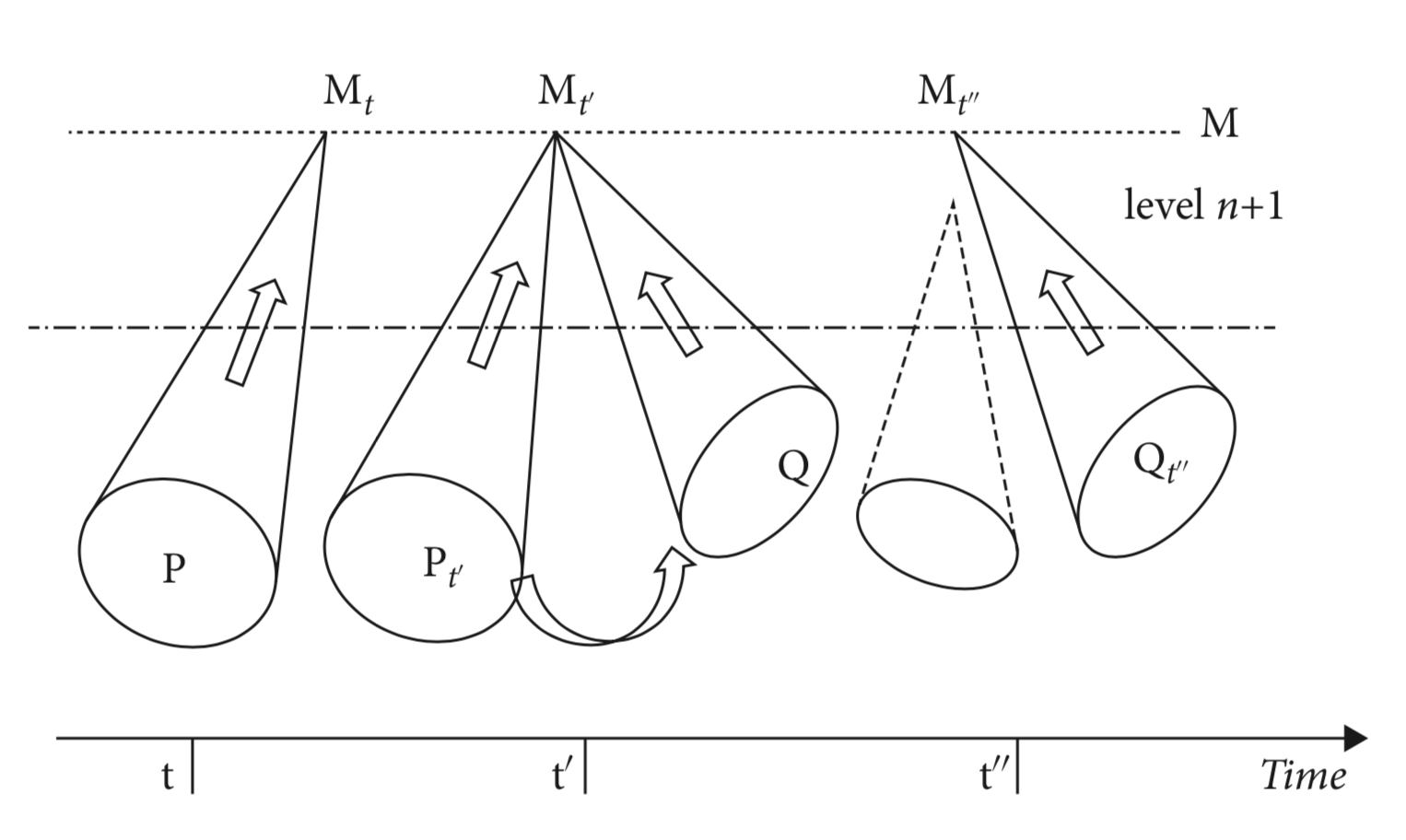
Emergence of complex links
Complexification
“Standard changes” of living systems (cf. René Thom): birth: (addition of new components), death (addition of certain components), collision (formation of new pattern bindings), scission (destruction of certain bindings).
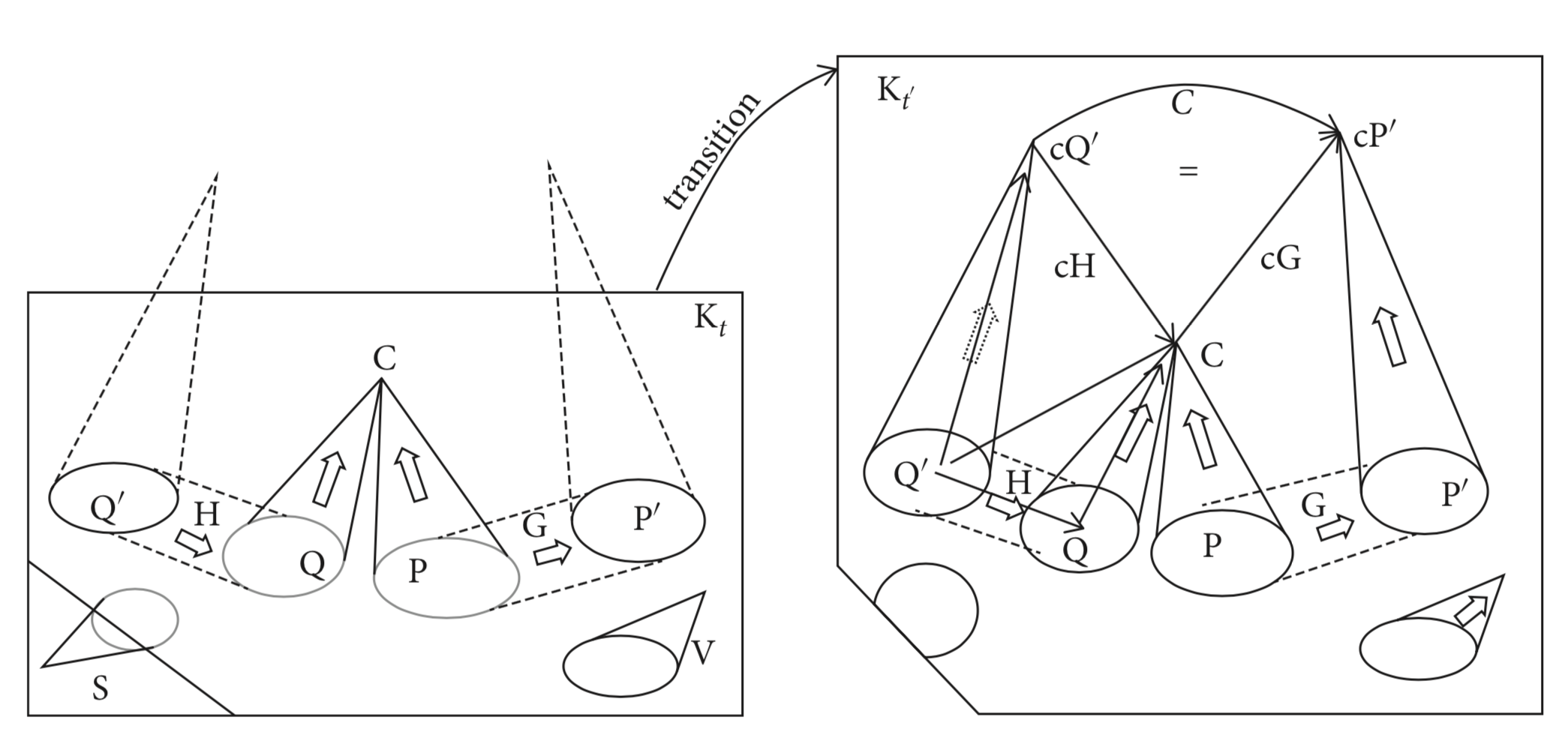
Emergence Theorem
Complexification preserves the Multiplicity Principle.
In a HES, there may be:
- formation of multi-faceted components more and more complex
- ⟶ emergence of complex links between them.
III. Memory Evolutive Neural Systems
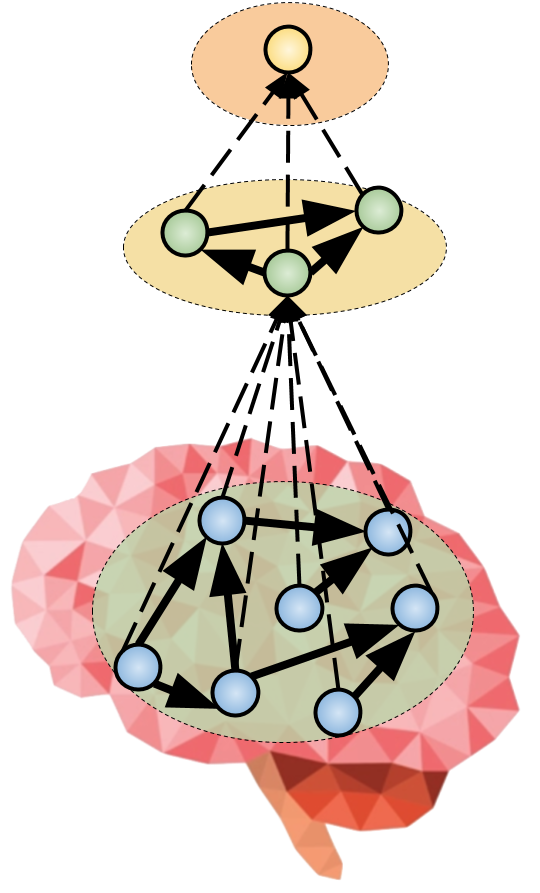
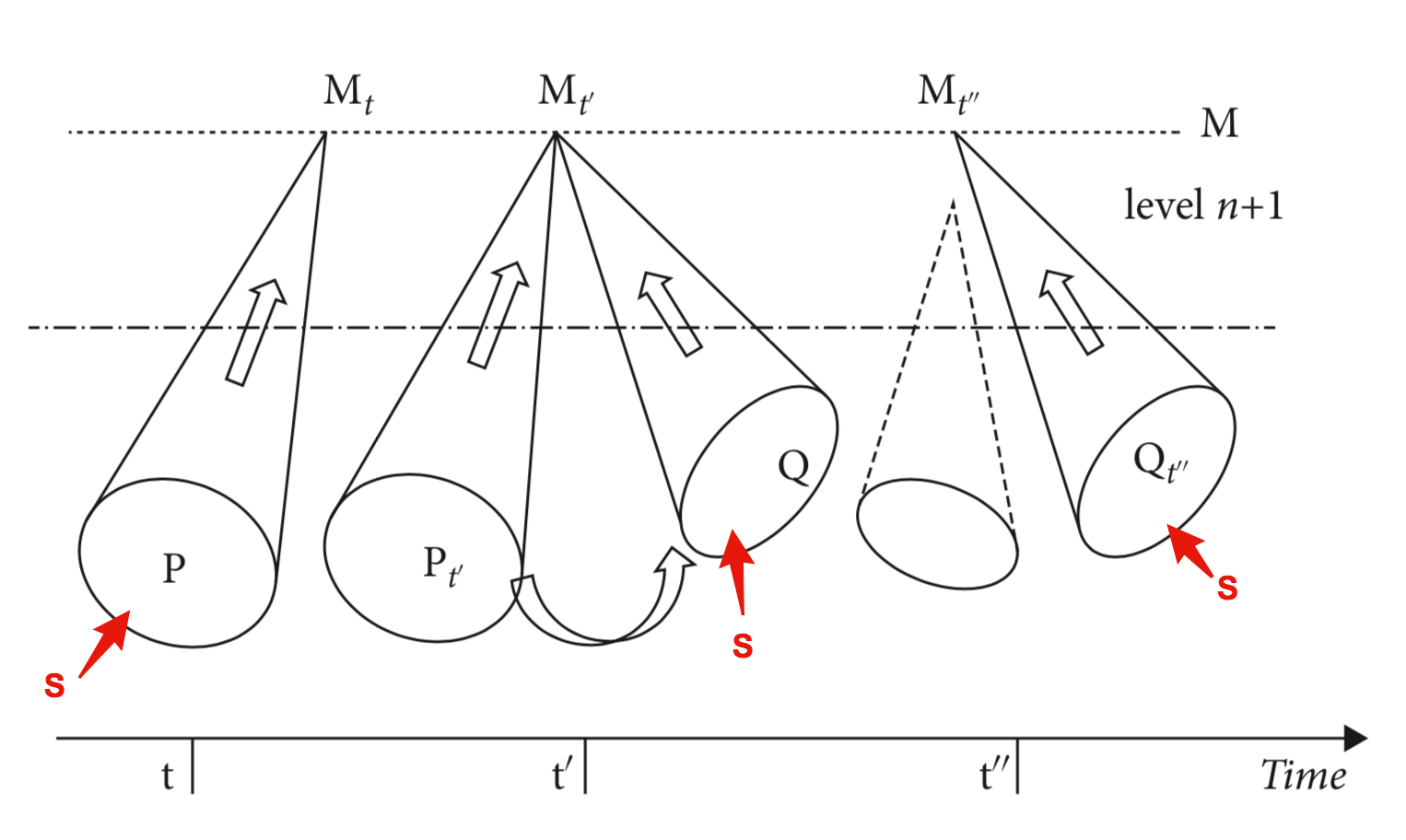
Flexible Memory
vs. Hopfield networks
- Hopfield rule:
-
to store patterns $\textbf{p}_1, ⋯, \textbf{p}_n$ in the Hopfield network, the weight matrix is set to:
$$W = \frac 1 N \sum\limits_{ i } \textbf{p}_i \textbf{p}_i^\T$$
cf. Jupyter Notebook for simulations
Hopfield networks:
- the stored patterns are not apparent in the network
- pattern capacity: $≃ 0.138 N$ (where $N$ is the number of neurons)
- no “flexibility”: if your mom’s appearance changes when she ages (which is unfortunately likely to happen), you don’t recognize her anymore!
- spurious patterns: linear combinations of odd number of patterns also stored!
- unoriented graph!