Work Environment

Department of Computer Science: University of Oxford

I.A. Historical Example

« […] you can build a mind from many little parts, each mindless by itself. »
Marvin Minsky, The Society of Mind (1986)

Marvin Minsky (1927-2016)		A.I. Researcher & Cognitive Scientist (MIT): A.I. Pioneer with John McCarthy Left his mark on popular culture: Adviser on Kubrick's 2001: A Space Odyssey Even appears in Digimon!

Minsky’s toy example

Playing with Blocks (Pb)

Calls two simpler mental agents:

1. Builder (B)

Vs…

2. Wrecker (W)

And when he's done Playing with his Blocks (Pb)   and   with his Dolls (Pd)

... he'd better tidy up! (T)

The mental agents here form an example of event structure:

… which can also be seen as a non-deterministic process:

choose 'Pb' or 'Pd' or ('Pb' and 'Pd'):
    if 'Pb':
        choose either 'B' or 'W':
if 'Pb' and 'Pd':
    launch 'T'

Event Structures:

• Domain theory ⟶ Programming Language Semantics

• Category Theory ⟶ Algebraic Effects

II. Event Structures as Domains

Well-founded poset   $E \eqdef \pair{\carrier E}{\leq_E}$:

poset such that $∀ \, e\in \carrier E, \quad \dc e \eqdef \underbrace{\lbrace e'\in\carrier E \mid e' \leq_E e \rbrace}_{\text{downward closure of } e}$     is finite.

Event structure   $E \eqdef \triple{\carrier E}{\leq_E}{\Con[E]}$:

1. a well-founded poset $(\carrier E, \underbrace{\leq_E}_{\rlap{\text{causal dependency relation}}})$ of events

2. a consistency relation $\Con[E] \subseteq \Pfin(E)$ such that:

   • $∀ \, e\in \carrier E, \quad \lbrace e \rbrace \in \Con[E]$
   • closure under subsets:     $X \subset Y \in \Con[E] \implies X \in \Con[E]$
   • augmentation property:     $x \in \Con[E] \; ∧ \; e' \leq_E e \in x \; ⟹ \; x \cup \lbrace e' \rbrace \in \Con[E]$

Playing child example

All the subsets of $\carrier E ≝ \lbrace {\rm Pb}, {\rm Pd}, \rm B, \rm T, \rm W\rbrace$ are in $\Con[E]$ except those containing $\lbrace \rm W, \rm B \rbrace$, or $\lbrace \rm W, \rm T \rbrace$.

Crucial concept:

Configurations = event history of a partial run of our computational process.

For that, we need two additional notions:

1. Consistent subsets

  Extends the definition of ‘being in the consistency relation’ to infinite subsets

2. Down-closed subsets:

  $x$ contains all the events that must have happened for any $e ∈ x$ to occur.

Configurations

Set of configurations:

$$\ConfStar[E] \eqdef \set{x \subseteq \carrier E \mid x \text{ consistent and down-closed} }$$

Notation:     $\Conf[E]$: Finite configurations

  $x$ contains all the events that entailed the point at which the partial run is, and no incompatible events.

Lemma: A (finite) subset is consistent ⟺ its downward closure is a (finite) configuration ⟺ it is a subset of a (finite) configuration.

Playing child: poset of configurations (inclusion order)

Rigid maps

Map of event structures $f: E \rightarrow F$:

a function $f: \carrier E \rightarrow \carrier F$   which is

• configuration preserving:     $x \in \Conf[E] \; ⟹ \; f[x] \in \Conf[F]$
• locally injective:     $x \in \Conf[E] \; ⟹ \; \Big(e_1, e_2 \in x \; ∧ \; f(e_1) = f(e_2) \in F \, ⟹ \, e_1 = e_2\Big)$

Rigid map of event structures:

a map which is also monotone

  local injectivity ⟹ “atomic” events (an event in $F$ can’t come from two consistent events in $E$)

Proposition: Maps are causality-reflecting on configurations:

$$\forall e_1, e_2 \in x \in \Conf[E], \quad f (e_1) \leq_F f (e_2) \Longrightarrow e_1 \leq_E e_2$$

⟹   for any rigid map $f$, $f[x]$ and $x$ are isomorphic as partial orders.

Proposition: Rigid maps are configuration-reflecting on configurations:

$$\forall x' \subseteq x \in \Conf[E], \; f[x'] \in \Conf[F] \Longrightarrow x' \in \Conf[E]$$

Thanks to the previous propositions, we can characterise rigid maps more “concretely”:

Lemma (Characterisation of Rigid maps): A map $f: E \rightarrow F$ is rigid iff

$$\forall x \in\Conf[E], \forall y \in \Conf[F], \quad y \subseteq f[x] \Longrightarrow \exists x' \in \Conf[E], \; x' \subseteq x \, \land \, f x' = y$$

Important example

For every well-founded poset $P$, $\triple{\carrier P}{\leq_P}{\Pfin(P)}$ is an event structure

When $P$ is finite $\leadsto$ elementary event structure, as $\carrier P ∈ \Con[P]$

A rigid map $f: P → Q$ between two posets seen as event structures is a monotonic function.

Quick categorical recap

Structures preserved by morphisms$\qquad \overset{\text{+ associativity, identity}}{\rightsquigarrow} \qquad \underbrace{\text{Category Theory}}_{\text{focus on relations rather than objects}}$

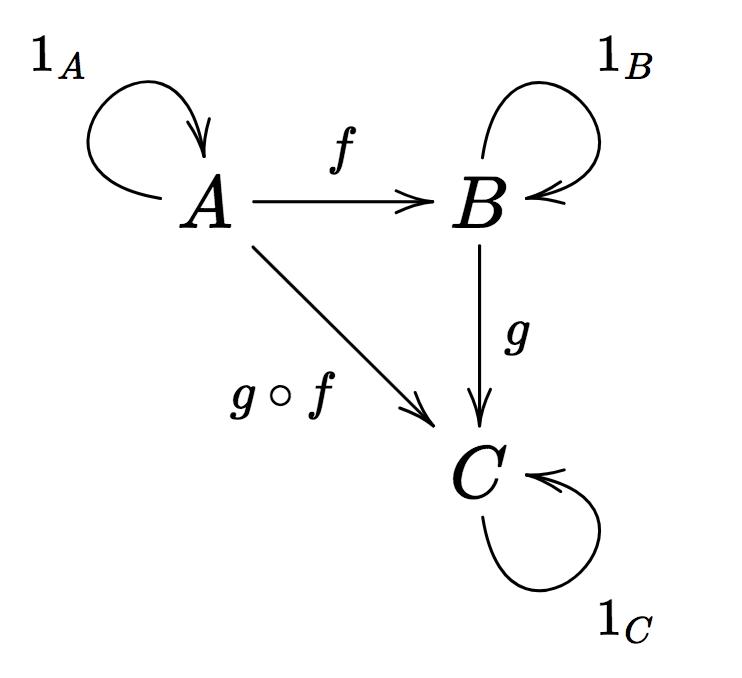
Examples:

• Objects preserved by morphisms:

  • Sets
  • Vector spaces, Topological spaces, Groups, Rings, Manifolds…
  • Logical formulas, Types (λ-calculus), …

• Structures forming one category:

  • Posets, Monoids, Groups, Groupoids, …

even (small) categories themselves form a category!

• Objects: Categories
• Morphisms: Functors

Domains

Scott domains: $x ≤ y$ ⟺ the information carried by $y$ "extends" the one of $x$

Category of finitary prime algebraic domains: $\PAD$

Let $D$ be a poset.

$X \subseteq \carrier D$ is finitely bounded:

iff $∀ \, y \in \Pfin(\carrier X)$, $y$ has an upper bound in $D$.

$D$ is consistently complete:

iff every finitely bounded subset $X$ has a least upper bound (lub) $\lub X$ in $D$.

If $D$ is consistently complete,   $p \in \carrier D$ is a complete prime:

iff for all $X \subset \carrier D$ bounded:

$$p \leq \lub X \implies \exists d \in X; \; p \leq d$$

Notation: $\dcp d ≝ \underbrace{\set{p \leq d \; \suchthat \; p \text{ complete prime}}}_{\text{prime downward-closure}}$

A prime algebraic domain:

is a consistently complete poset $D$ that satisfies the prime algebraicity property: for every $d \in \carrier D, \; d = \lub \dcp d$.

Example: Posets and their complete primes (circled)

Other examples and non-examples:

• $\unit ≝ [0,1]$ is not a prime algebraic domain.
• the ordinal $\omega + 1 := \set{0 \leq 1 \leq 2 \leq \cdots \leq \omega}$ is a prime algebraic domain.
• ${(\omega + 1)}^2$ (component-wise order) is a prime algebraic domain

Finitary prime algebraic domain:

if $\dcp p$ is finite for every complete prime $p$.

Prime algebraic domain morphisms

Map of prime algebraic domains $f : C \to D$:

is a monotone function such that for every finitely bounded $X \subset \carrier C$, $\lub f[X] = f\,\lub X$.

  Generalised Scott continuous functions: preserve the lubs of directed sets, but also those of finitely bounded sets.

Notation: Category of finitary prime algebraic domains and their maps: $\PAD$

Event structures as Finitary prime algebraic domains

Lemma (from event structures to prime algebraic domains): Let $E$ be an event structure. The poset $\pair{\ConfStar[E]}{\subset}$ is a prime algebraic domain, whose complete primes are the configurations $\lbrace \dc e \rbrace_{e ∈ \carrier E}$.

Conversely:

Lemma (from prime algebraic domains to event structures): Let $D$ be a finitary prime algebraic domain, we have an event structure $\CP_D$ given by:

• $\carrier {\CP_D} := \set{p \in \carrier D \; \suchthat \; p \text{ complete prime}}$
• $p_1 \leq_{\CP_D} p_2 \iff p_1 \leq_D p_2$
• $x \in \Con[\CP_D] \iff x \text{ bounded in } \carrier D$

Lastly, going back and forth between these two constructions:

Lemma:

$$∀ \, E ∈ \ES, \; E ≅ \CP_{\ConfStar[E]} \quad \qquad \quad ∀ \, D ∈ \PAD, \; D ≅ \pair{\ConfStar[\CP_D]}{\subset}$$

Playing child: Finitary prime algebraic domain of configurations (complete primes underlined)

Event Structures as Presheaves

Natural transformations:

Functor morphisms

Yoneda embedding:

$$\yoneda_{\catC}: \begin{cases} \catC \to \overbrace{\Psh{\catC} ≝ [\opposite\catC, \Set]}^{\smash{\text{Category of Presheaves}}} \\ C \mapsto \Hom[\catC]{-, C} \end{cases}$$

Yoneda Lemma: For every presheaf $P ∈ \Psh{\catC}$, there is an isomorphism:

$$\begin{align*} &\Hom[\Psh{\catC}]{\yoneda_\catC(C), P} ≅ P(C) && \text{(natural in } C, P\text{)}\end{align*}$$

Examples: Cayley’s theorem, Dedekind–MacNeille completion, Skip-gram Model in ML, …

Universal constructions

Natural transformations ≃ functor morphisms

Examples

Limits:

• Terminal objects

  

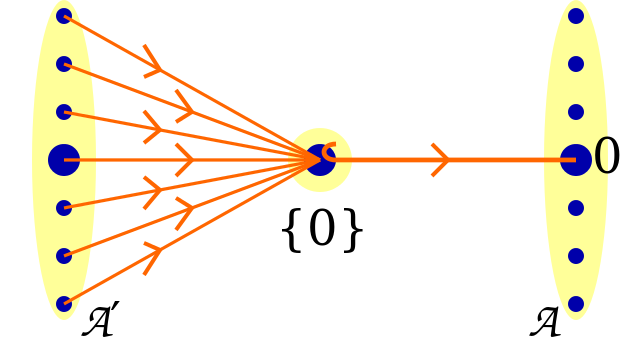
• Products

  

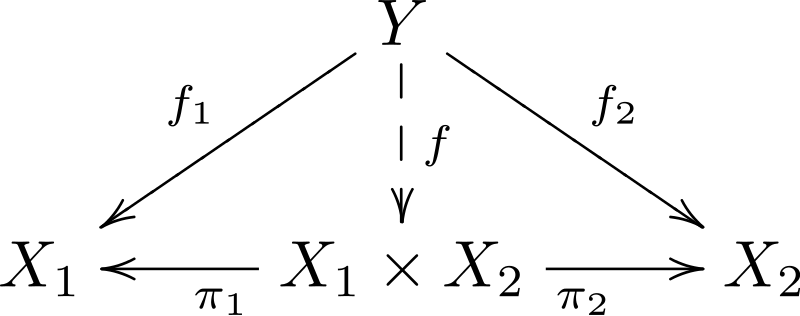
• Equalizers (Kernels), Pullbacks, …

Colimits:

• Initial objects

• Coproducts

  

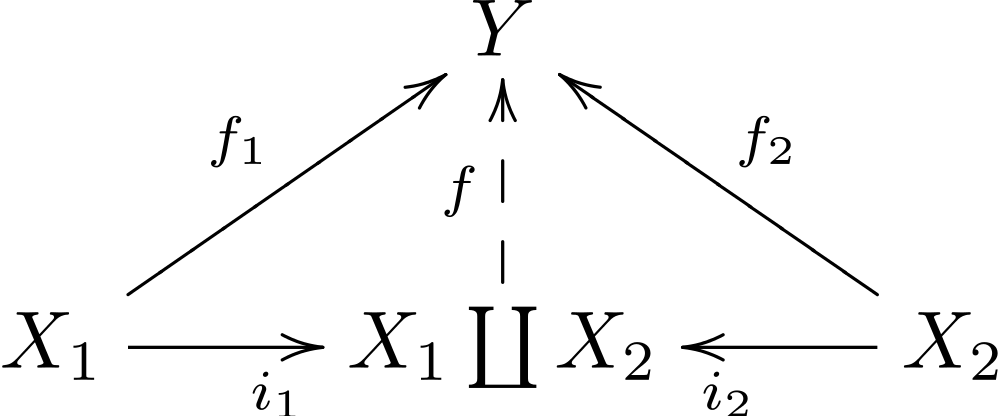
• Coequalizers (Quotients), Pushouts, …

A colimit of a functor $D: I ⟶ \C$ (called a diagram) is an initial object in the category of natural transformations from $D$ to a constant functor (the category of cocones).

Category of elements $\elem P$ of a presheaf $P ∈ \Psh\catC$:

• objects are pairs $\pair C x$, where $C ∈ \catC$ and $x ∈ PC$
• morphisms $\pair C x → \pair C {x'}$ are $\catC$-morphisms $f: C → C'$ such that $P f (x') = x$

Presheaves as cocompletion

Let $\C$ be a small category and $\yoneda_\C: \C ⟶ \Psh\C$ its Yoneda embedding.

Theorem (Free Cocompletion of $\C$):

For every cocomplete category $\catD$ and functor $F :\C \to \catD$, there is a unique (up to isomorphism) cocontinuous functor $\hat F: \Psh\C \to \catD$ making the following triangle commute up to natural isomorphism:

A puzzling question:

What does freely adding all its colimits to $\C$ have to do with presheaves over $\C$?

It can be shown that every diagram $D$ is "equivalent" to a diagram $D'$ that has the property:

$$\Comma{\yoneda_\C {D'}}{P_{D'}} ≅ \overbrace{\Comma{\yoneda_\C}{P_{D'}}}^{≅ \, \elem {P_{D'}}}$$

And the freely added colimit of $D$ in $\Psh\C$ will be taken to be the presheaf $P_{D'}$.

Any diagram $D: I ⟶ \C$ is "equivalent" to the diagram $\elem(\colim \yoneda_\C D) \xto U \C$, where $U$ is the forgetful functor. Thus:

Theorem (Every presheaf is a canonical colimit of representables): For all $P ∈ \Psh\C$,

$$P \, ≅ \, \colim\Big(\Comma{\yoneda_\C}{P} \xto U \C \xto {\yoneda_\C} \Psh\C\Big)$$

Density formula/co-Yoneda lemma

Different take on the matter: through the lens of coends, which are universal extranatural transformations from a constant functor.

Theorem (co-Yoneda lemma): For every presheaf $P ∈ \Psh\C$:

$$P ≅ \int^c Pc × \yoneda_\C c$$

This is a particular case of tensor product of functors:

if $F ∈ \Psh\C$ and $G: \C ⟶ \catD$ where $\catD$ is cocomplete:

$$F \otimes_{\C} G ≝ \int^c F(c) \cdot G(c)$$

Tensor product intuition

Let’s picture

• $\C$-objects as nonshiny Lego blocks
• their corresponding representables as the shiny versions
• $\catD$-objects as real-world physical objects.
  
  

1. $F$ (colimit of representables) = a shiny Lego construction/gluing
2. $G$ turns each nonshiny Lego block into a real-world $\catD$-object

Then

$F \otimes_{\C} G$ = real-world gluing where each shiny Lego block in $F$ is replaced by the image of the nonshiny corresponding Lego block by $G$.

The co-Yoneda lemma: $P \, ≅ \, P \otimes_{\C} \yoneda_\C$

Of course! Replacing each shiny Lego block in $P$ by itself yields $P$ again!

Kan Extensions

Kan extensions: very expressive universal constructions that extend functors along one another.

« The notion of Kan extensions subsumes all the other fundamental concepts of category theory. » (MacLane)

Left Kan extension of a functor $F: \catC → \catD$ along a functor $K: \catC → \wC$:

is a functor $\Lan K F: \wC → \catD$ and a natural transformation $η: F → \Lan K F \circ K$ which is an initial arrow from $F ∈ [\catC, \catD]$ to $- \circ K: [\wC, \catD] → [\catC, \catD]$.

In other words: for any $G: \wC → \catD$ and $γ: F → GK$, there exists a unique natural transformation $α: \Lan K F → G$ such that $α_K \circ η = γ$:

Theorem (Existence of Kan extensions along a functor into a cocomplete category):

Let $\C$ be a small category, and $K: \C → \wC, \, F: \C → \catD$ be functors.
If $\catD$ is cocomplete, $\Lan K F$ exists and can be defined, for all $\tilde C ∈ \wC$, as:

$$\Lan K F (\tilde C) ≝ \colim\Big(\Comma K {\tilde C} \xto U \C \xto F \catD\Big)$$

On top of that, if $F$ is fully faithful, the natural transformation $η: F → \Lan K F \circ K$ is an isomorphism.

With the machinery of Kan extensions, we have as corollaries:

• the fact that presheaves are colimits of representables

• the free cocompletion theorem

• the Yoneda and co-Yoneda lemmas (with Kan extensions as coends)

Nerve construction

« The nerve construction is inherent in the theory of categories » (Tom Leinster)

Nerve-Realisation paradigm:

Let $F: \C ⟶ \catD$ be a functor from a small category to locally small cocomplete one.

• The left Kan extension of $F$ along $\yoneda_\C$ is referred to as Yoneda extension or the realisation functor of $F$
• It has a right adjoint $\Nerve F ≝ \underbrace{D ⟼ \Hom[\catD]{F(-), D}}_{\text{denoted by } \Hom[\catD]{F(=), -}}$ called the nerve of $F$:
  
  

$$\Lan{\yoneda_{\C}}{F} ⊣ \Nerve F \cong \Lan F {\yoneda_{\C}}$$

Nerve-Realisation paradigm intuition: let’s bring back our Lego blocks

You can think of

• $\C$-objects as being Lego blocks – and thus $\Psh\C$-objects
  as being Lego constructions due to $\Psh\C$ being the free cocompletion of $\C$

• $\D$-objects as being real-world physical objects.

Then:

• the functor $F$ turns each Lego block into a real-world object.
• the realisation functor of $F$ takes a Lego construction and replaces each of its Lego block by their real-world counterpart given by $F$
• the nerve functor of $F$ associates to every real-world object the "closest matching" Lego construction for this object, by giving a way to probe the object with every Lego block.

For example, our child may have a bust of Newton in his bedroom (the bust being an object of $\catD$ in our comparison), and may
suddenly feel like making a Lego copy of it, thereby acting like the nerve:

Nerve of the inclusion of finite paths into event structures

The nerve of the inclusion functor $\Path+ \stackrel{I_+}{\hookrightarrow} \ES$ enables us to
regard event structures as presheaves over non-empty paths.

$\Nerve {I_+}$ is fully faithful, due to $I_+$ being dense:

A functor $F: \catC ⟶ \catD$ is said to be dense/co-dense if for all $C ∈ \catC$:

$$C \; ≅ \; \colim\Big(\Comma F C \xto U \catC \xto F \catD\Big) \; / \; C \; ≅ \; \lim\Big(\Comma C F \xto U \catC \xto F \catD\Big)$$

and the fact that:

If $\C \stackrel{i}{\hookrightarrow} \catD$ is dense, the nerve functor $\Nerve i$ is fully faithful.

… that we can obtain as a corollary of this theorem:

Theorem: If $F: \catC → \catD$ is a functor, $G: \catC → \catD$ a continuous functor and $\catA \overset{i}{\hookrightarrow} \catC$ a co-dense subcategory, there is a unique extension of every natural transformation $αi: Fi → Gi$ to a natural transformation $α: F → G$.

To reuse the Lego analogy, $\C$ being dense in $\catD$ can be understood as the the Lego bricks being so small (let’s say of atomic size!) that the Lego constructions are faithful enough to distinguish any two non-isomorphic real-world objects!