Signalling pathways and causal depth

Generating deep signalling pathways with refinements

Yvan Sraka & Younesse Kaddar

Github Repo

I. Biological context

II. Theoretical Model

III. Refinements

IV. Implementation

I. Biological context

Why does evolution favor deep signalling pathways?

I. Biological context

Why does evolution favor deep signalling pathways?

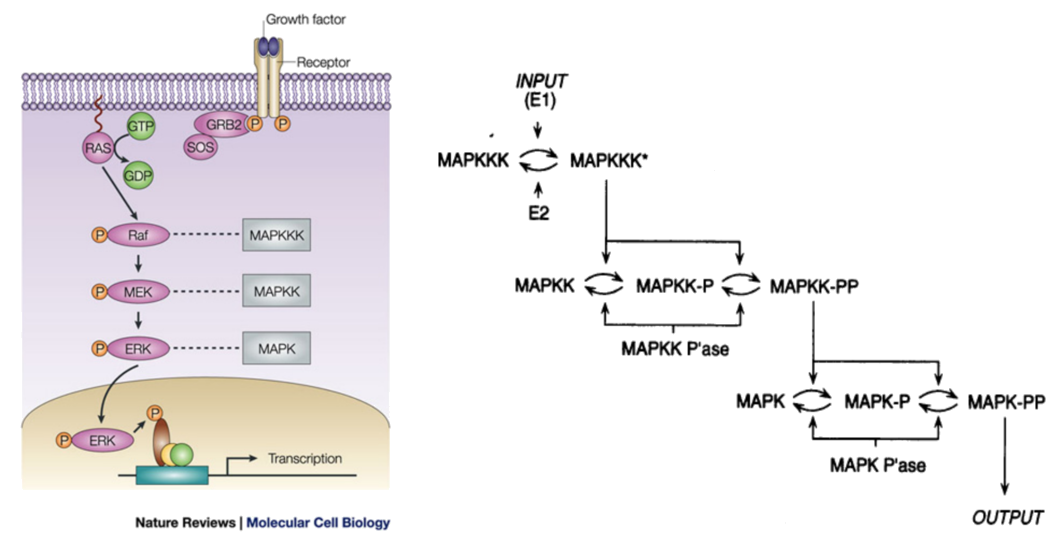
Example: the MAPK/ERK pathway

Animation courtsey of Ribosome Studio Youtube channel

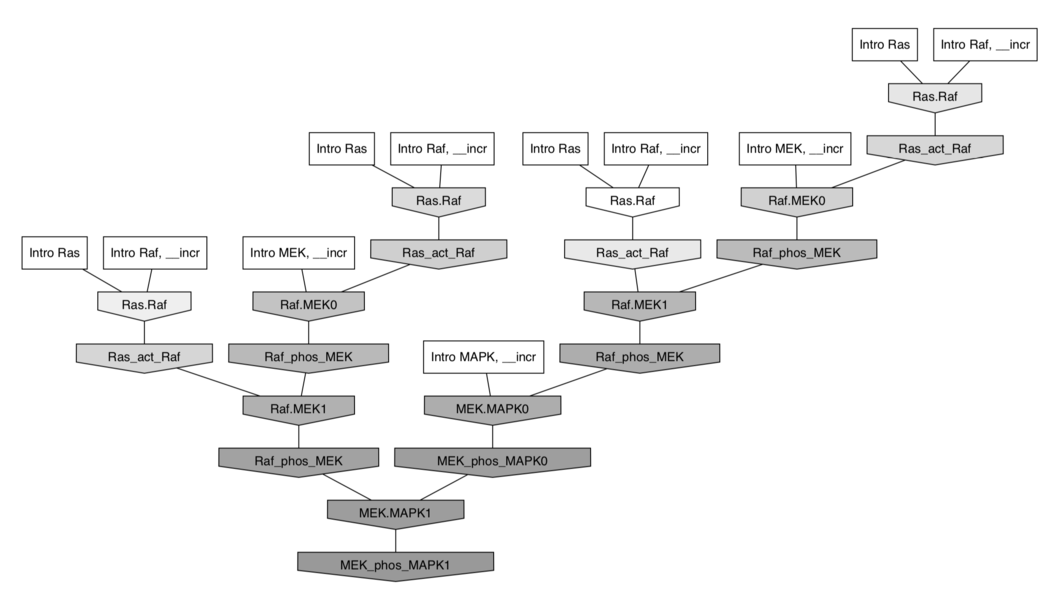
*MAPK/ERK Signalling Pathway* - Simplified overview

$⇓ \;$ in Kappa

*Simplified MAPK/ERK causal flow* - KaFlow-generated story

Why does evolution favor deep signalling pathways?

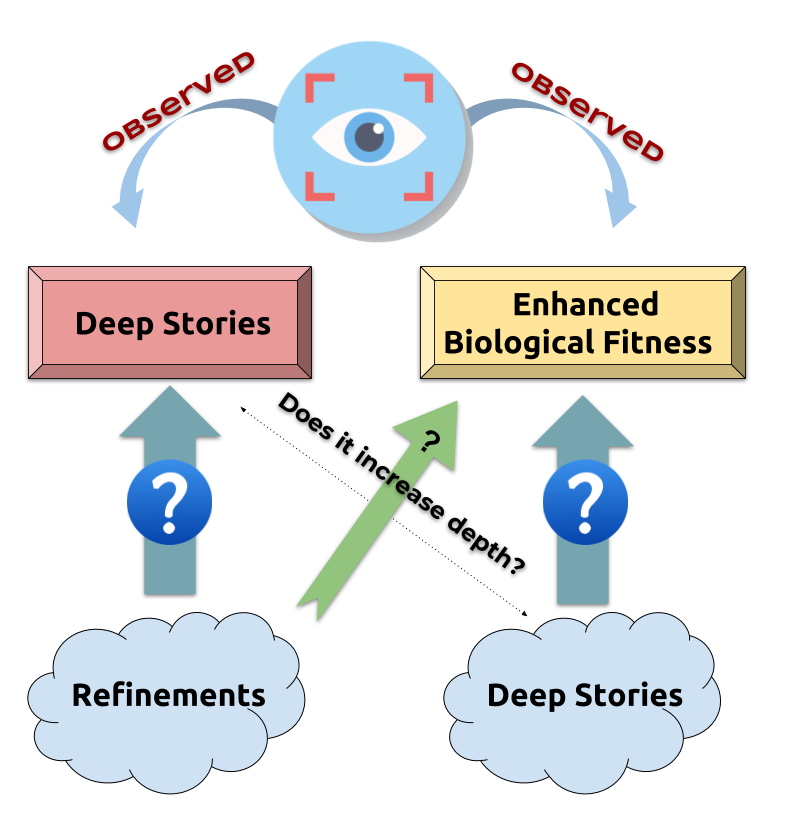
Natural selection: Deeper stories $⟹$ Improving biological fitness

BUT counter-intuitive

energetically
probabilistically: Indeed: if

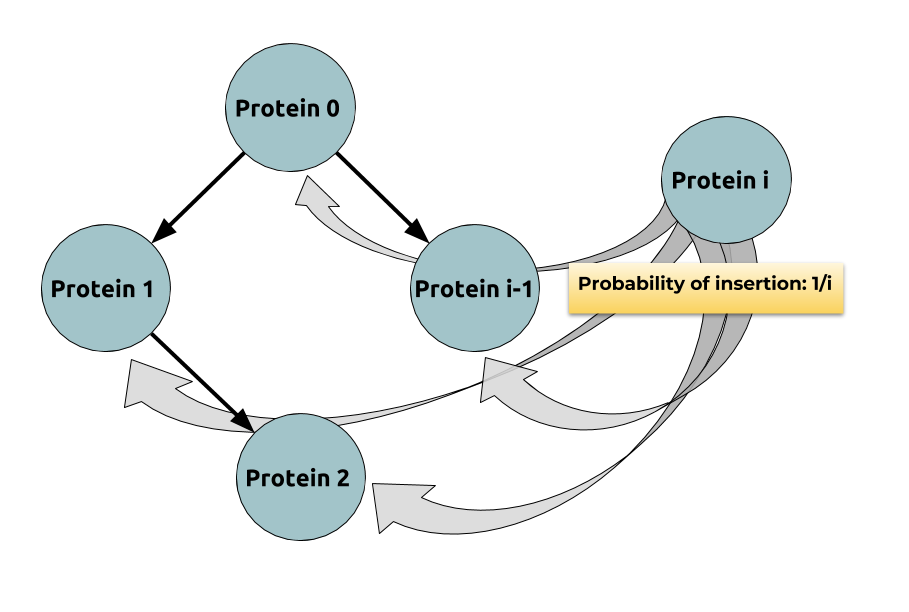$$ \begin{align*} & 𝔼(\max_i \depth(P_i)) \\ & ≤ 𝔼\Big(\ln\Big(\underbrace{\sum\limits_{ i=0 }^n \exp(\depth(P_i))}_{\; ≝ \; α_n}\Big)\Big) \\ & ≤ \ln \underbrace{𝔼(α_n)}_{\rlap{\substack{= \; 𝔼(α_{n-1}) + 𝔼(\exp(\depth(P_n))) \\ = \, (1 + \frac e i) \, 𝔼(α_{n-1})}}}\\ & = \ln \Big(\prod\limits_{ i=1 }^n \Big(\underbrace{1 + \frac e i}_{≤\, \exp (\frac e i)}\Big) \Big) = e H_n \sim \boxed{e \ln n} \end{align*} $$

Possible explanations:

Greater depth:: $$\, \\ \\ \\ \begin{cases} \text{ enhances stability } \\ \text{ deletions make pathways non-functional more often than additions do } \end{cases}$$

II. Theoretical model

Does refinement increase depth?

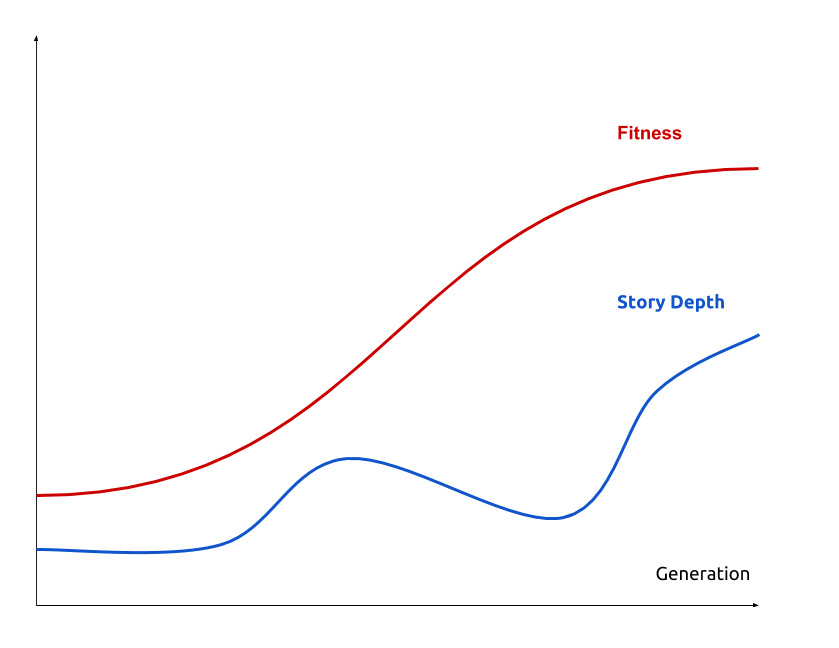
Genetic algorithm

An heuristic optimisation that loop on two steps:

MUTATION: map ancesters to $n$ descendent with random mutations
SELECTION: filter descendent on their fitness (ERK quantity)

Model biais: biological clock assumption, spontaneous discrete generation, etc …

$$\MEK(x_{pp}), \MAPK(x_{p}) ⟶_{τ_b} \MEK(x_{pp}^{\color{DeepPink}{1}}), \MAPK(x_{p}^{\color{DeepPink}{1}})\\ \color{DarkCyan}{\MEK(x_{pp}^1), \MAPK(x_{p}^1) ⟶_{τ_u} \MEK(x_{pp}), \MAPK(x_{p})}\\ \MEK(x_{pp}^1), \MAPK(x_{p}^1) ⟶_{τ_p} \MEK(x_{pp}^1), \color{OrangeRed}{\MAPK(x_{pp}^1)}\\$$

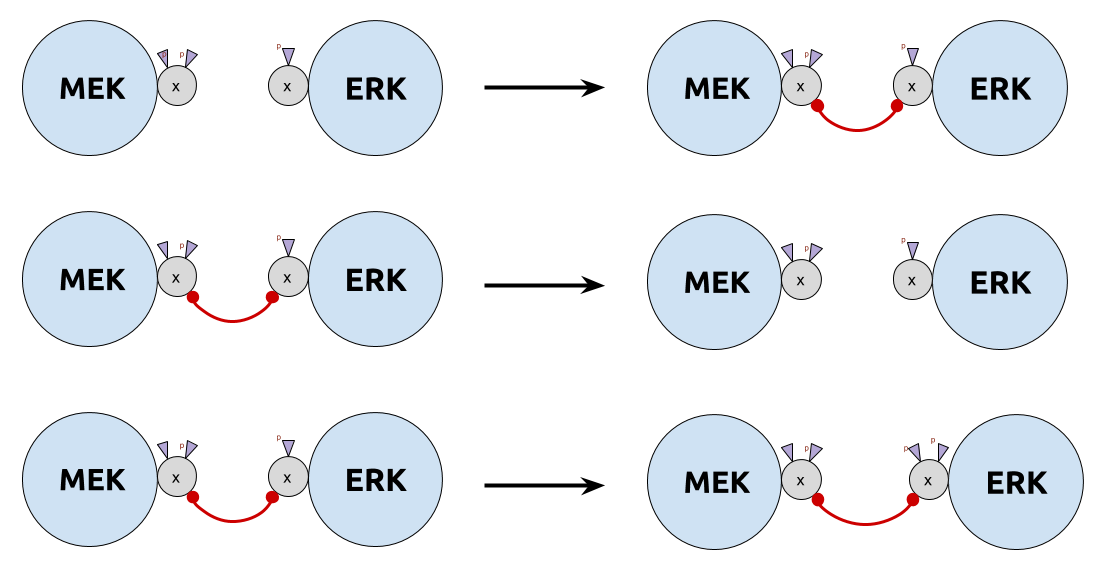
$\color{DarkCyan}{τ_u}$ too big: unbind before phosphorylation (too liquid)
$\color{DarkCyan}{τ_u}$ too small: never unbind (too sticky)

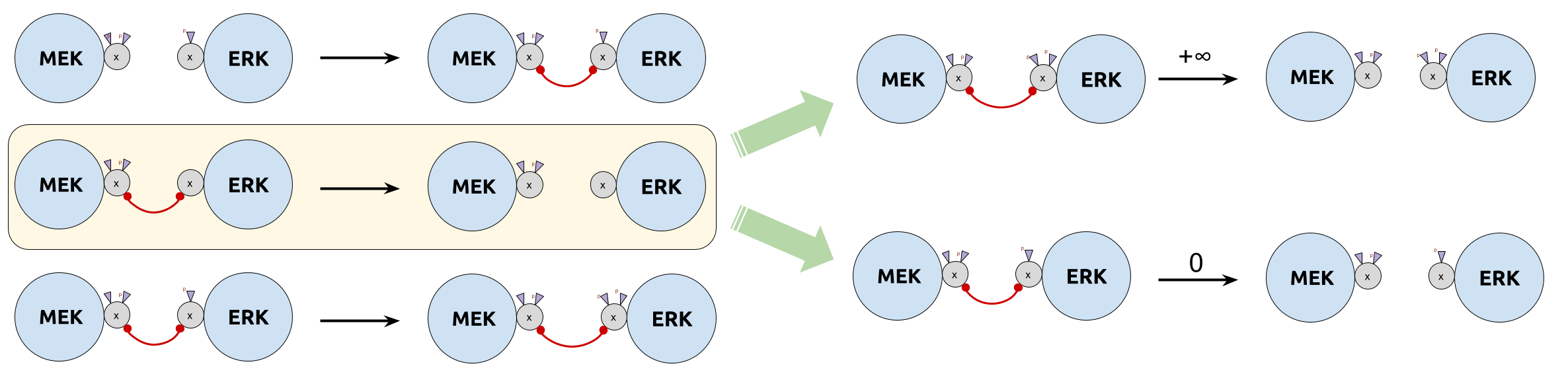
Category of site graphs: $\SGph$

Objects $(V, λ, σ, μ)$:

$V$: set of nodes
$λ: V ⟶ 𝒜$: name assignment
$σ: V ⟶ 𝒫(𝒮)$: site assignment
$μ: \underbrace{\text{ matching}}_{\rlap{\text{irreflexive symmetric binary relation}}}$ over $\sum\limits_{ v ∈ V } σ(v)$

Morphism $f: (V, λ, σ, μ) ⟶ (V', λ', σ', μ')$:

Name/site/edge-preserving and edge reflecting monomorphism $f: V ⟶ V'$

Signature $Σ: 𝒜 ⟶ 𝒮$:

$x ≤ Σ \quad ⟺ \quad σ_x(V_x) ⊆ Σ(λ_x(V_x))$
$Σ ≤ x \quad ⟺ \quad Σ(λ_x(V_x)) ⊆ σ_x(V_x)$

Epimorphisms

Forgetful functor to the category of graphs:: $$U: \SGph ⟶ \Gph$$
Epimorphisms from $x$ to $y$:: $$[x, y]^e \; ≝ \; \big\lbrace h ∈ \underbrace{\Hom[\SGph]{x, y}}_{\text{denoted by } [x,y]} \; \mid \; h \text{ is an epi (i.e. right-cancellable)} \big\rbrace$$

Lemma:
$$h ∈ \overbrace{\Hom[\SGph]{x, y}}^{\text{denoted by } [x,y]} \text{ is an epi } \\ \; ⟺ \; ∀ c_y ⊆ y \text{ connected component}, \, h^{-1}(c_y) ≠ ∅$$

Epi-mono factorisation

Factorisation:: $f ∈ [s, x]$ is said to be factored by $t$ if $f = γ ϕ$ for $ϕ ∈ [s, t]^e$ and $γ ∈ [t, x]$

Every iso $α ∈ [t, t']$ conjugates the factorisations $ϕ, γ$ and $ϕ', γ'$:

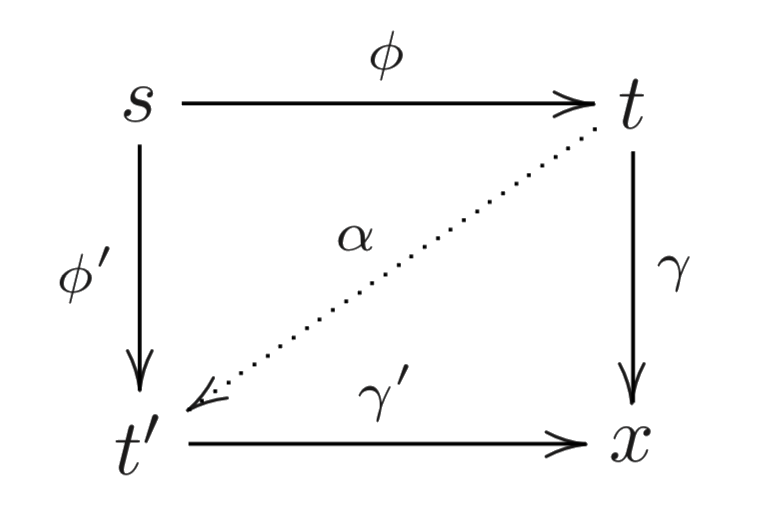
⟹ Equivalence relation:

$$ϕ, γ \; ≃_{tt'} \; ϕ', γ'$$

The group $[t, t]$ acts freely on $[s, t]^e × [t, x]$ (as we have epis and monos), so by Burnside’s lemma:

$$\vert \underbrace{[s, t]^e × [t, x] / [t, t]}_{\text{denoted by } [s, t]^e ×_{[t, t]} [t, x]} \vert = \frac 1 {\vert [t,t] \vert} \sum\limits_{ (ϕ, γ) ∈ [s, t]^e × [t, x]} \underbrace{\vert Stab_{[t, t]}((ϕ, γ)) \vert}_{= 1} \\ = \vert [s, t]^e × [t, x] \vert/\vert [t,t] \vert$$

Object refinement

A refinement $Σ(s)$ of $s ≤ Σ$ under $Σ$:: is a set comprised of one element per isomorphism class in $\lbrace t : Σ \; \mid \; [s, t]^e ≠ ∅ \rbrace$

Theorem: if $s ≤ Σ$ and $x : Σ$:

$$[s,x] \; ≅ \; \sum\limits_{ t ∈ Σ(s) } [s, t]^e ×_{[t,t]} [t, x]$$

Rule refinement

Well defined atomic action (in a rewriting rule):

edge addition/deletion (when permitted), agent addition/deletion

Labelled transition:

$$x \quad ⟶_f^R \quad f(α) \cdot x$$

where

the rule $R \; ≝ \; \underbrace{s}_{\text{object}}, \underbrace{α}_{\text{action}}, \underbrace{τ}_{\text{rate}}$, whose activity $a(x, r) \; ≝ \; τ \vert [s, x] \vert$
$f ∈ [s, x]$

If $θ$ is an iso: $θ(r) \; ≝ \; θ(s), θ(α), τ$ satisfies:

$$x \, ⟶_f^R \, f(α) \cdot x \qquad ⟺ \qquad x \, ⟶_{fθ^{-1}}^{θ(R)} \, fθ^{-1}(θ(α)) \cdot x$$

Rule refinement:
If $s ≤ Σ$, the refinement of the rule $R \; ≝ \; s, α, τ$ under $Σ$ is:

$$Σ(s, α, τ) \; ≝ \; (t, ϕ(α), τ)_{t ∈ Σ(s), ϕ ∈ [s,t]^e/[t,t]}$$

IV. Methods

Our naive code implementation was split between:

KaSimir: Genetic algorithm implementation, using KaSim to compute fitness
KaStorama: wrapper around KaStor to retreive causal story depth from KaSim traces
KaRapuce: Slitghly change rates of refined rules as mutation event

https://github.com/yvan-sraka/KaSimir

Demo time!

Bibliography

P. Boutillier, J. Feret, J. Krivine, and W. Fontana, “The Kappa Language
and Kappa Tools,” p. 52.
“Signaling Pathways,” Tocris Bioscience. https://www.tocris.com/signaling-pathways.
V. Danos, J. Feret, W. Fontana, R. Harmer, and J. Krivine, “Rule-Based
Modelling, Symmetries, Refinements,” in Formal Methods in Systems
Biology, vol. 5054, J. Fisher, Ed. Berlin, Heidelberg: Springer Berlin
Heidelberg, 2008, pp. 103–122.
E. Murphy, V. Danos, J. Féret, J. Krivine, and R. Harmer, “Rule-Based
Modeling and Model Refinement,” in Elements of Computational Systems
Biology, H. M. Lodhi and S. H. Muggleton, Eds. Hoboken, NJ, USA: John
Wiley & Sons, Inc., 2010, pp. 83–114.
“List of signalling pathways,” Wikipedia. 30-Nov-2016.